Contents
【問題】
【難易度】★★★☆☆(普通)
図1は三相サイリスタ変換器の応用例を示す。負荷側サイリスタ変換器に接続される負荷の電圧が確立すると安定な運転ができるので,例として回転している同期電動機を示している。次の問に答えよ。
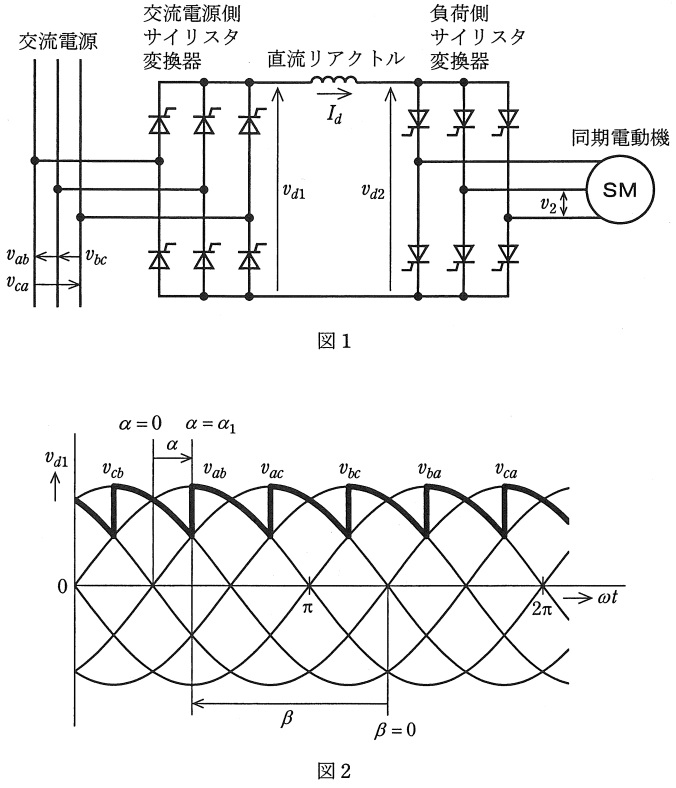
(1) 運転のモードとして,交流電源から負荷に電力を供給する力行モード及び負荷から交流電源に電力を戻す回生モードがある。それぞれのモードにおいて,交流電源側,負荷側それぞれのサイリスタ変換器の直流電圧平均値\( \ V_{d1} \ \mathrm {[V]} \ \),\( \ V_{d2} \ \mathrm {[V]} \ \)は正,負のいずれであるか。ただし,図示する方向の極性を正とする。
(2) 直流電流はリプルがなく一定の電流\( \ I_{d} \ \mathrm {[A]} \ \)とし,負荷側の交流線間電圧\( \ v_{2} \ \)は実効値\( \ V_{2} \ \mathrm {[V]} \ \)の正弦波電圧波形とする。このとき,負荷側サイリスタ変換器は,重なり角が無視できて,一般の三相サイリスタ変換器と同様の表記として制御進み角\( \ \beta _{2} \ \mathrm {[rad]} \ \)で運転しているものとする。実効値\( \ V_{2} \ \mathrm {[V]} \ \)と制御進み角\( \ \beta _{2} \ \mathrm {[rad]} \ \)を使って表す直流電圧平均値\( \ V_{d2} \ \mathrm {[V]} \ \)の式を,その導出過程を含めて示せ。
なお,図2は制御遅れ角\( \ \alpha =\alpha _{1} \ \)で運転している交流電源側サイリスタ変換器の動作を線間電圧波形を用いて示した図であり,式を導出する際の参考にされたい。一般に制御進み角\( \ \beta \ \mathrm {[rad]} \ \)は,\( \ \beta =\pi – \alpha \ \mathrm {[rad]} \ \)の関係があるので,\( \ \beta =0 \ \)のタイミングは図2に示すようになる。
(3) このとき,負荷側サイリスタ変換器の損失を零として,力行モードで負荷に供給している有効電力の平均値\( \ P_{2} \ \mathrm {[W]} \ \)を電流\( \ I \ \mathrm {[A]} \ \)と制御進み角\( \ \beta _{2} \ \mathrm {[rad]} \ \)を使って式で示せ。
【ワンポイント解説】
サイクロコンバータのメカニズムに関する問題です。
サイリスタ整流回路のメカニズムを理解している方であれば,選択しても良い問題かなと思います。
最初はとっつきにくい内容かもしれませんが,理解してしまえば計算間違いもほぼなく\( \ 10 \ \)分程度で解けてしまうお得な問題となります。
1.三相サイリスタブリッジ整流回路の動作
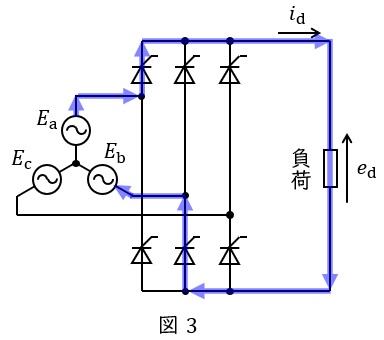
三相サイリスタブリッジ整流回路は図3のように\( \ 6 \ \)つのサイリスタを接続した回路で,サイリスタがオンするタイミングで一番電圧の高い相から一番電圧の低い相に電流が流れ,出力されます。
例えば\( \ E_{\mathrm {a}} \ \)が一番電圧が高く,\( \ E_{\mathrm {b}} \ \)が一番電圧が低い場合には図3に示すように電流が流れ\( \ e_{\mathrm {d}}=E_{\mathrm {a}}-E_{\mathrm {b}} \ \)が出力されます。
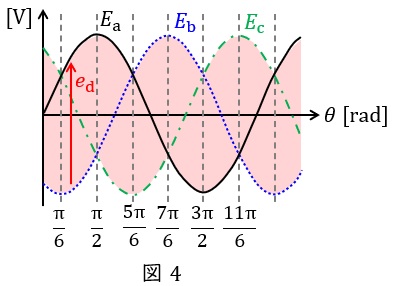
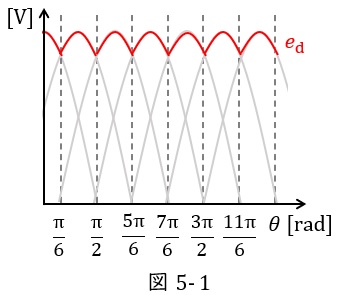
したがって,制御角\( \ \alpha =0 \ \)のときは図4に示した電圧\( \ e_{\mathrm {d}} \ \)が出力となり,電圧の波形の変化をまとめると図5-1のようになり,その平均電圧\( \ E_{\mathrm {d}} \ \)は基準電圧を\( \ E_{\mathrm {a}}=\sqrt {2}E\sin \omega t \ \)とすると,
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \left( E_{\mathrm {a}}-E_{\mathrm {b}}\right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \left\{ \sqrt {2}E\sin \omega t-\sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \right\} \mathrm {d}\omega t \\[ 5pt ]
\end{eqnarray}
\]
となります。ここで和積の公式\( \ \displaystyle \sin A-\sin B=2\cos \frac {A+B}{2}\sin \frac {A-B}{2} \ \)より,
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right)\sin \frac {\pi}{3} \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right) \frac {\sqrt {3}}{2}\mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \sqrt {6}E \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\left[ \sin \left( \omega t-\frac {\pi}{3} \right) \right] _{\frac {\pi}{6}}^{\frac {\pi}{2}} \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \left( \frac {\pi}{2}-\frac {\pi}{3} \right)- \sin \left( \frac {\pi}{6}-\frac {\pi}{3} \right)\right\} \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \frac {\pi}{6}- \sin \left( -\frac {\pi}{6} \right)\right\} \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\left\{ \frac {1}{2}- \left( -\frac {1}{2} \right)\right\} \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E \\[ 5pt ]
\end{eqnarray}
\]
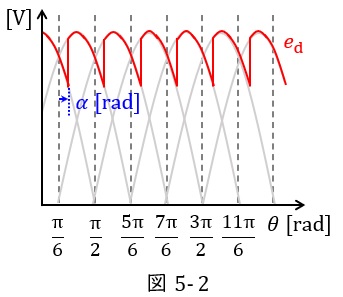
と求められます。同様に制御角\( \ \alpha >0 \ \)のときは図5-2に示すような出力電圧となり,
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \left( E_{\mathrm {a}}-E_{\mathrm {b}}\right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3}{\pi }\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \left\{ \sqrt {2}E\sin \omega t-\sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \right\} \mathrm {d}\omega t \\[ 5pt ]
E_{\mathrm {d}} &=&\frac {3}{\pi }\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right)\sin \frac {\pi}{3} \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3}{\pi }\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right) \frac {\sqrt {3}}{2}\mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3}{\pi }\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \sqrt {6}E \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\left[ \sin \left( \omega t-\frac {\pi}{3} \right) \right] _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \left( \frac {\pi}{2}+\alpha -\frac {\pi}{3} \right)- \sin \left( \frac {\pi}{6}+\alpha -\frac {\pi}{3} \right)\right\} \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \left( \alpha +\frac {\pi}{6} \right)- \sin \left( \alpha -\frac {\pi}{6} \right)\right\} \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\cdot 2\cos \alpha \sin \frac {\pi }{6} \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\cdot 2\cos \alpha \cdot \frac {1}{2} \\[ 5pt ]
&=&\frac {3\sqrt {6}}{\pi }E\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
2.サイクロコンバータ
サイクロコンバータは周波数の異なる交流の電力変換を行うことができる装置です。定比式サイクロコンバータと連続式サイクロコンバータがあります。
\( \ 2 \ \)組の逆並列接続した変換器は,電流の向きを切り替えるときに電源の短絡が発生しないよう電流休止期間が必要で,出力周波数の上限は入力周波数の\( \ \displaystyle \frac {1}{2} \ \)程度となります。
①定比式サイクロコンバータ
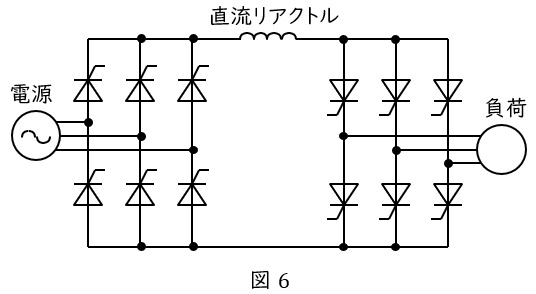
図6のように,\( \ 2 \ \)組の全波整流回路を使用して,それぞれの整流回路を交互に動作させることにより,周波数の異なる交流電力を得る方式です。
回路構成が簡単ですが,出力波形がひずみやすいという特徴があります。
②連続式サイクロコンバータ
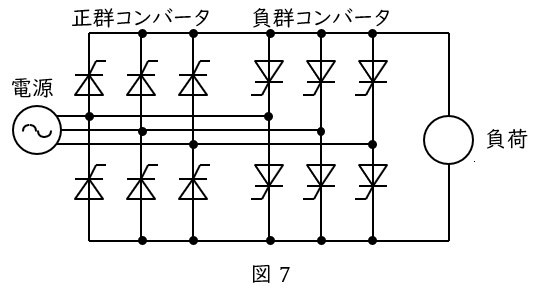
図7のように,正群コンバータと負群コンバータの\( \ 2 \ \)群のコンバータで素子を点弧制御して出力を得る方式です。
正群コンバータの素子と負群コンバータを順に作動させることで,負荷電圧の平均値が正弦波になるように制御することが可能となります。(綺麗な正弦波が得られる訳ではありません。)
【解答】
(1)力行モード及び回生モードにおいて,\( \ V_{d1} \ \mathrm {[V]} \ \),\( \ V_{d2} \ \mathrm {[V]} \ \)は正,負のいずれか
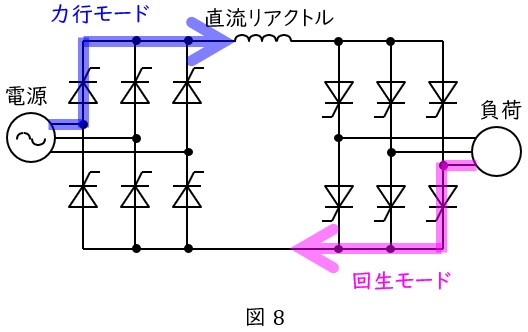
図8に示すように力行モード及び回生モードでは電圧の極性は逆となり,力行モードでは\( \ V_{d1} \ \mathrm {[V]} \ \),\( \ V_{d2} \ \mathrm {[V]} \ \)ともに正,回生モードでは\( \ V_{d1} \ \mathrm {[V]} \ \),\( \ V_{d2} \ \mathrm {[V]} \ \)ともに負,となります。
(2)実効値\( \ V_{2} \ \mathrm {[V]} \ \)と制御進み角\( \ \beta _{2} \ \mathrm {[rad]} \ \)を使って表す直流電圧平均値\( \ V_{d2} \ \mathrm {[V]} \ \)の式
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作」と同様に,制御遅れ角\( \ \alpha =\alpha _{1} \ \)で力行モードの時の直流電圧平均値\( \ V_{d1} \ \mathrm {[V]} \ \)は,線間電圧が相電圧の\( \ \sqrt {3} \ \)倍であることに注意すると,
\[
\begin{eqnarray}
V_{d1} &=&\frac {3\sqrt {6}}{\pi }\frac {V_{1}}{\sqrt {3}}\cos \alpha _{1} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{1}\cos \alpha _{1} \\[ 5pt ]
\end{eqnarray}
\]
となる。負荷側のサイリスタ変換器においては極性が逆なので上式の電圧\( \ V_{1}→-V_{2} \ \)及び制御遅れ角\( \ \alpha _{1}→ \ \)制御進み角\( \ \pi -\beta _{2} \ \)に置き換えれば良いので,
\[
\begin{eqnarray}
V_{d2} &=&\frac {3\sqrt {2}}{\pi }\left( -V_{2}\right) \cos \left( \pi -\beta _{2}\right) \\[ 5pt ]
&=&-\frac {3\sqrt {2}}{\pi }V_{2} \left( \cos \pi \cos \beta _{2} +\sin \pi \sin \beta _{2} \right) \\[ 5pt ]
&=&-\frac {3\sqrt {2}}{\pi }V_{2} \left( -\cos \beta _{2} +0 \right) \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{2} \cos \beta _{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)力行モードで負荷に供給している有効電力の平均値\( \ P_{2} \ \mathrm {[W]} \ \)
負荷側サイリスタ変換器での損失がないので,負荷に供給している有効電力は,直流電力と等しい。したがって,
\[
\begin{eqnarray}
P_{2} &=&V_{d2}I_{d} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{2} \cos \beta _{2}I_{d} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{2}I_{d} \cos \beta _{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは