Contents
【問題】
【難易度】★★★☆☆(普通)
図1に示す単相\( \ \mathrm {PWM} \ \)制御電圧形インバータは,定格交流電流\( \ 30 \ \mathrm {[A]} \ \),直流電圧\( \ E_{\mathrm {d}}=150 \ \mathrm {[V]} \ \)であり,リアクタンス\( \ X=0.4 \ \mathrm {[\Omega ]} \ \)のリアクトル(抵抗は,無視できるものとする。)を介して電圧\( \ V_{\mathrm {L}}=100 \ \mathrm {[V]} \ \)の交流電源に連系している。このインバータに次の信号\( \ s \ \)
\[
\begin{eqnarray}
s &=& K\sin \left( \omega t+\phi \right) \\[ 5pt ]
\end{eqnarray}
\]
を入力したとき,インバータにおける出力交流電圧の基本波瞬時値\( \ v_{\mathrm {v}} \ \)は,次になるものとする。
\[
\begin{eqnarray}
v_{\mathrm {v}} &=& E_{\mathrm {d}}\cdot K\sin \left( \omega t+\phi \right) \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
ここで,\( \ K \ \):変調率\( \ \left( 0≦K≦1 \right) \ \)(\( \ 1 \ \)まで可能なものとする。)
\( \ \omega \ \):交流電源の角周波数
\( \ \phi \ \):交流電源電圧の位相を基準とした\( \ v_{\mathrm {v}} \ \)の位相角
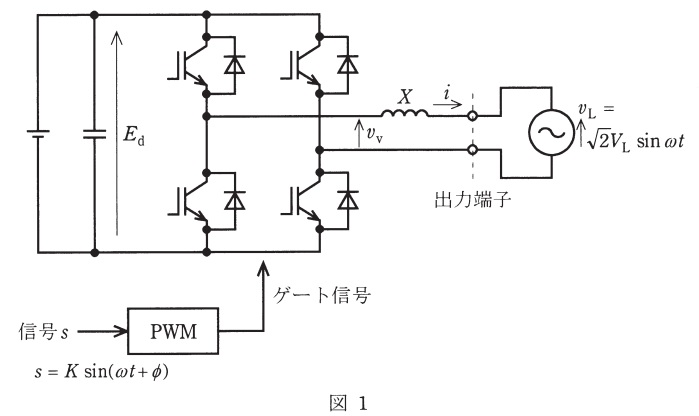
このインバータで交流電流\( \ i \ \)を出力したときの動作について次の問に答えよ。ただし,高調波は考えないものとする。
(1) フェーザで表したインバータ出力電流\( \ \dot I \ \),交流電源電圧\( \ V_{\mathrm {L}} \ \)(位相の基準としているので実数で表示)及び\( \ X \ \)を用いて,インバータ出力電圧\( \ {\dot V}_{\mathrm {v}} \ \)を求める式を示せ。
(2) このインバータが図1に示す出力端子において\( \ 3 \ \mathrm {[kW]} \ \)の有効電力を力率\( \ 1 \ \)で出力している。このとき,次の値を求めよ。
a.\( \ {\dot V}_{\mathrm {v}} \ \)の大きさ\( \ V_{\mathrm {v}} \ \mathrm {[V]} \ \)(実効値)
b.\( \ K \ \)
c.\( \ \tan \phi \ \)
(3) このインバータを力率\( \ 1 \ \)以外でも運転するものとする。出力電流\( \ \dot I \ \)を実数分\( \ I_{\mathrm {P}} \ \)と虚数分\( \ I_{\mathrm {Q}} \ \)とに分けて\( \ \dot I=I_{\mathrm {P}}+\mathrm {j}I_{\mathrm {Q}} \ \)と表す。\( \ I_{\mathrm {P}} \ \),\( \ I_{\mathrm {Q}} \ \),\( \ V_{\mathrm {L}} \ \)及び\( \ X \ \)を用いて\( \ V_{\mathrm {v}} \ \mathrm {[V]} \ \)の値を求める式を示せ(絶対値の記号を付けただけでは不可。その値を求める式とする。)。
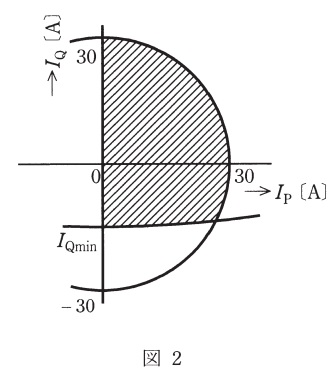
(4) \( \ I_{\mathrm {P}} \ \)及び\( \ I_{\mathrm {Q}} \ \)の出力可能な範囲は,図2の網掛け範囲となる。\( \ \dot I \ \)の大きさ(実効値)\( \ I \ \mathrm {[A]} \ \)は,定格電流である\( \ 30 \ \mathrm {[A]} \ \)に制限される。\( \ I_{\mathrm {P}} \ \)は,インバータとして正の範囲(零を含む)に限定している。このほか,上記(3)の\( \ V_{\mathrm {v}} \ \)の値を求める式で,\( \ V_{\mathrm {v}} \ \)が\( \ K=1 \ \)のときの値\( \ \displaystyle \frac {E_{\mathrm {d}}}{\sqrt {2}} \ \mathrm {[V]} \ \)に制限されることによっても電流の範囲が制限される。\( \ I_{\mathrm {P}}=0 \ \mathrm {[A]} \ \)における\( \ I_{\mathrm {Q}} \ \)の最小値\( \ I_{\mathrm {Qmin}} \ \mathrm {[A]} \ \)の値を求めよ。
【ワンポイント解説】
単相インバータの原理と各諸計算に関する問題です。
インバータは直流を交流にするもので,電圧形インバータはコンデンサにより入力電圧を一定とさせることを目的としたものとなります。本問では出題されていませんが,電流形インバータはリアクトルを交流電源に直列に接続して,入力電流を一定とさせることを目的としたものとなります。
1.\( \ \mathrm {PWM} \ \)制御と変調率
\( \ \mathrm {PWM} \ \)制御はパルス幅変調制御を意味し,出力の交流電圧をパルス幅で制御する方法となります。
出力電圧は交流電源の搬送波と信号波の大きさの比較により行います。
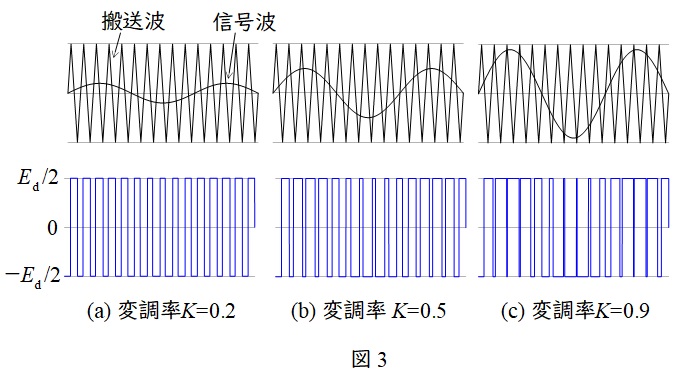
変調率は搬送波と信号波の比率をいい,図3のように搬送波と信号波の比率を変化させることで,出力電圧のパルス幅を変化させることができます。
【解答】
(1)出力電流\( \ \dot I \ \),交流電源電圧\( \ V_{\mathrm {L}} \ \)及び\( \ X \ \)を用いて,インバータ出力電圧\( \ {\dot V}_{\mathrm {v}} \ \)を求める式
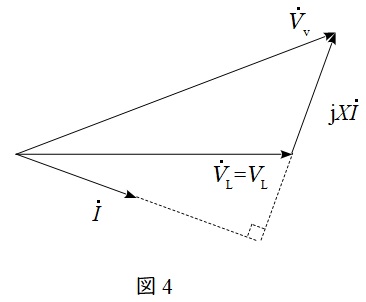
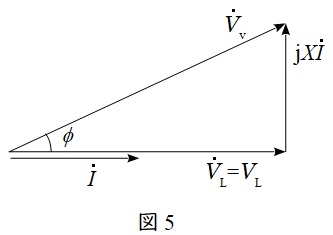
フェーザ図は図4のようになるので,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {v}}&=& V_{\mathrm {L}}+\mathrm {j}X\dot I \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)a.\( \ {\dot V}_{\mathrm {v}} \ \)の大きさ\( \ V_{\mathrm {v}} \ \mathrm {[V]} \ \)
題意より,有効電力\( \ P=3 \ \mathrm {[kW]} \ \),力率\( \ \cos \theta =1 \ \),出力電流\( \ I=30 \ \mathrm {[A]} \ \)なので,
\[
\begin{eqnarray}
P&=& V_{\mathrm {L}}I \\[ 5pt ]
V_{\mathrm {L}}&=&\frac {P}{I} \\[ 5pt ]
&=&\frac {3\times 10^{3}}{30} \\[ 5pt ]
&=&100 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,三平方の定理より,
\[
\begin{eqnarray}
V_{\mathrm {v}}&=& \sqrt {{V_{\mathrm {L}}}^{2}+\left( XI \right) ^{2}} \\[ 5pt ]
&=& \sqrt {100^{2}+\left( 0.4\times 30 \right) ^{2}} \\[ 5pt ]
&=& \sqrt {10144} \\[ 5pt ]
&≒&100.72 → 101 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)b.変調率\( \ K \ \)
インバータにおける出力交流電圧の瞬時値\( \ v_{\mathrm {v}} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {v}} &=& E_{\mathrm {d}}\cdot K\sin \left( \omega t+\phi \right) \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
で与えられているので,その実効値\( \ V_{\mathrm {v}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {v}} &=& \frac {E_{\mathrm {d}}\cdot K}{\sqrt {2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。これを\( \ K \ \)について整理して各値を代入すると,
\[
\begin{eqnarray}
K &=& \frac {\sqrt {2}V_{\mathrm {v}}}{E_{\mathrm {d}}} \\[ 5pt ]
&=& \frac {\sqrt {2}\times 100.72}{150} \\[ 5pt ]
&≒& 0.94960 → 0.950 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)c.\( \ \tan \phi \ \)
\[
\begin{eqnarray}
\tan \phi &=& \frac {XI}{V_{\mathrm {L}}} \\[ 5pt ]
&=& \frac {0.4\times 30}{100} \\[ 5pt ]
&=& 0.120 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ I_{\mathrm {P}} \ \),\( \ I_{\mathrm {Q}} \ \),\( \ V_{\mathrm {L}} \ \)及び\( \ X \ \)を用いて\( \ V_{\mathrm {v}} \ \mathrm {[V]} \ \)の値を求める式
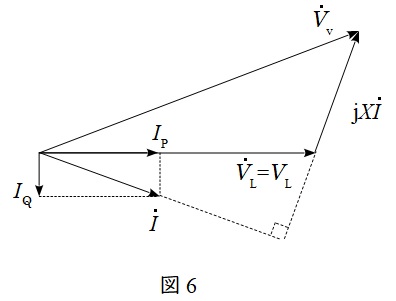
題意に沿ってフェーザ図を描くと図6のようになる。図6より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {v}}&=& V_{\mathrm {L}}+\mathrm {j}X\dot I \\[ 5pt ]
&=& V_{\mathrm {L}}+\mathrm {j}X\left( I_{\mathrm {P}}+\mathrm {j}I_{\mathrm {Q}}\right) \\[ 5pt ]
&=& V_{\mathrm {L}}+\mathrm {j}XI_{\mathrm {P}}-XI_{\mathrm {Q}} \\[ 5pt ]
&=& \left( V_{\mathrm {L}}-XI_{\mathrm {Q}}\right) +\mathrm {j}XI_{\mathrm {P}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その大きさ\( \ V_{\mathrm {v}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {v}}&=& \sqrt {\left( V_{\mathrm {L}}-XI_{\mathrm {Q}}\right) ^{2}+\left( XI_{\mathrm {P}}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ I_{\mathrm {P}}=0 \ \mathrm {[A]} \ \)における\( \ I_{\mathrm {Q}} \ \)の最小値\( \ I_{\mathrm {Qmin}} \ \mathrm {[A]} \ \)
題意に示されている\( \ V_{\mathrm {v}} \ \)の最大値は\( \ K=1 \ \)のときの値\( \ \displaystyle \frac {E_{\mathrm {d}}}{\sqrt {2}} \ \mathrm {[V]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {v}}&≦& \frac {E_{\mathrm {d}}}{\sqrt {2}} \\[ 5pt ]
\sqrt {\left( V_{\mathrm {L}}-XI_{\mathrm {Q}}\right) ^{2}+\left( XI_{\mathrm {P}}\right) ^{2}}&≦& \frac {E_{\mathrm {d}}}{\sqrt {2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,このときの\( \ I_{\mathrm {Q}} \ \)の最小値が\( \ I_{\mathrm {Qmin}} \ \)となる。したがって,\( \ I_{\mathrm {P}}=0 \ \mathrm {[A]} \ \)の条件から,
\[
\begin{eqnarray}
\sqrt {\left( V_{\mathrm {L}}-XI_{\mathrm {Q}}\right) ^{2}}&≦& \frac {E_{\mathrm {d}}}{\sqrt {2}} \\[ 5pt ]
V_{\mathrm {L}}-XI_{\mathrm {Q}}&≦& \frac {E_{\mathrm {d}}}{\sqrt {2}} \\[ 5pt ]
XI_{\mathrm {Q}}&≧& V_{\mathrm {L}}-\frac {E_{\mathrm {d}}}{\sqrt {2}} \\[ 5pt ]
I_{\mathrm {Q}}&≧& \frac {\displaystyle V_{\mathrm {L}}-\frac {E_{\mathrm {d}}}{\sqrt {2}}}{X} \\[ 5pt ]
&=& \frac {\displaystyle 100-\frac {150}{\sqrt {2}}}{0.4} \\[ 5pt ]
&≒& -15.165 → -15.2 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より,進み無効電流を正としているので,\( \ I_{\mathrm {Qmin}}=15.2 \ \mathrm {[A]} \ \)(遅れ)と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは