Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
定格一次電圧\( \ 66 \ \mathrm {[kV]} \ \),定格二次電圧\( \ 6.6 \ \mathrm {[kV]} \ \)の\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)\( \ \mathrm {2} \ \)台の変圧器がある。変圧器\( \ \mathrm {A} \ \)の定格容量は\( \ 20 \ \mathrm {[MV\cdot A]} \ \),百分率リアクタンス降下は\( \ 12 \ \mathrm {[%]} \ \)である。一方,変圧器\( \ \mathrm {B} \ \)の定格容量は\( \ 10 \ \mathrm {[MV\cdot A]} \ \)で,百分率リアクタンス降下は不明である。これら\( \ \mathrm {2} \ \)台の変圧器を定格二次電圧で並行運転したところ,負荷電力が\( \ 22.5 \ \mathrm {[MV\cdot A]} \ \)となったところで変圧器\( \ \mathrm {B} \ \)が定格容量に達した。励磁電流及び抵抗分は無視するものとして,次の値を求めよ。
(1) 変圧器\( \ \mathrm {B} \ \)の百分率リアクタンス降下(自己容量基準)\( \ \mathrm {[%]} \ \)
(2) この負荷条件における電圧変動率\( \ \mathrm {[%]} \ \)。ただし,負荷力率は\( \ 0.8 \ \)(遅れ)とする。
【ワンポイント解説】
変圧器の並行運転に関する問題です。
電圧変動率の近似式を知っていたら大チャンスの問題です。
近似式は電圧変動率の定義式から導出は可能ですが,試験時間を考えると基本的に覚えるしかありませんので,覚えるようにして下さい。
1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス(パーセントインピーダンス)\( \ %Z \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.百分率インピーダンスの容量換算
「1.オーム法からパーセントインピーダンス法への変換」の通り,百分率インピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \mathrm {[V\cdot A]} \ \)の時\( \ %Z_{\mathrm {A}} \ \mathrm {[%]} \ \)のインピーダンスを\( \ P_{\mathrm {B}} \ \mathrm {[V\cdot A]} \ \)へ換算した百分率インピーダンス\( \ %Z_{\mathrm {B}} \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}%Z_{\mathrm {A}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.変圧器の負荷分担
並行運転の条件を満たす同じ基準容量の元での百分率インピーダンス\( \ %Z_{\mathrm {A}} \ \mathrm {[%]} \ \)の変圧器\( \ \mathrm {A} \ \)と百分率インピーダンス\( \ %Z_{\mathrm {B}} \ \mathrm {[%]} \ \)の変圧器\( \ \mathrm {B} \ \)があり,負荷\( \ P \ \mathrm {[W]} \ \)を接続するとき,それぞれの負荷分担\( \ P_{\mathrm {A}} \ \mathrm {[W]} \ \)及び\( \ P_{\mathrm {B}} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&\frac {%Z_{\mathrm {B}}}{%Z_{\mathrm {A}}+%Z_{\mathrm {B}}}P \\[ 5pt ]
P_{\mathrm {B}}&=&\frac {%Z_{\mathrm {A}}}{%Z_{\mathrm {A}}+%Z_{\mathrm {B}}}P \\[ 5pt ]
\end{eqnarray}
\]
と求められます。両変圧器とも一次二次電圧が等しいことから,分流の法則が適用できるという解釈で考えると良いかと思います。
4.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)
変圧器の一次二次を合算した二次側換算の抵抗成分を\( \ R=\displaystyle \frac {r_{1}}{a^{2}}+r_{2} \ \),一次二次を合算した二次側換算のリアクタンス成分を\( \ X=\displaystyle \frac {x_{1}}{a^{2}}+x_{2} \ \)とし,定格二次電圧を\( \ V_{\mathrm {2n}} \ \mathrm {[V]} \ \),定格二次電流を\( \ I_{\mathrm {2n}} \ \mathrm {[A]} \ \)とすると,百分率抵抗降下\( \ p \ \mathrm {[%]} \ \)及び百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
p &=&\frac {RI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
q &=&\frac {XI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
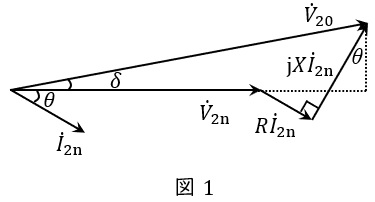
定格負荷(遅れ力率\( \ \cos \theta \ \))を接続したときの変圧器のベクトル図は図1のように描くことができ,電圧変動率\( \ \varepsilon \ \)は上記\( \ p \ \),\( \ q \ \)を用いると,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&≃&p\cos \theta + q\sin \theta +\frac {1}{200}\left( q\cos \theta -p\sin \theta \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と近似することができ,\( \ {\dot V}_{\mathrm {20}} \ \)と\( \ {\dot V}_{\mathrm {2n}} \ \)の位相差が十分に小さく,\( \ \varepsilon \ \)が\( \ 4 % \ \)以下の場合には,
\[
\begin{eqnarray}
\varepsilon &≃&p\cos \theta + q\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
と近似することができます。
【解答】
(1)変圧器\( \ \mathrm {B} \ \)の百分率リアクタンス降下(自己容量基準)\( \ \mathrm {[%]} \ \)
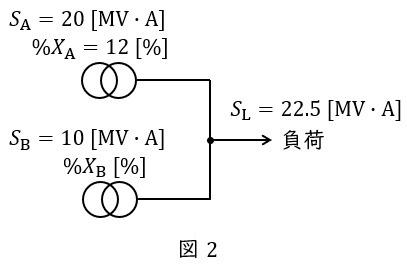
変圧器の並行運転の単線結線図を描くと図2のようになる。
図2において,変圧器\( \ \mathrm {A} \ \)の百分率リアクタンス\( \ %X_{\mathrm {A}}=12 \ \mathrm {[%]} \ \)を\( \ 10 \ \mathrm {[MV\cdot A]} \ \)換算した値\( \ %X_{\mathrm {A}}^{\prime } \ \mathrm {[%]} \ \)は,ワンポイント解説「2.百分率インピーダンスの容量換算」の通り,
\[
\begin{eqnarray}
%X_{\mathrm {A}}^{\prime }&=&\frac {10}{20}\times %X_{\mathrm {A}} \\[ 5pt ]
&=&\frac {10}{20}\times 12 \\[ 5pt ]
&=&6 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となり,このとき変圧器\( \ \mathrm {B} \ \)が定格容量\( \ \left( 10 \ \mathrm {MV\cdot A}\right) \ \)に達したので,ワンポイント解説「3.変圧器の負荷分担」の通り,
\[
\begin{eqnarray}
S_{\mathrm {B}}&=&\frac {%X_{\mathrm {A}}^{\prime }}{%X_{\mathrm {A}}^{\prime }+%X_{\mathrm {B}}}\cdot P_{\mathrm {L}} \\[ 5pt ]
10&=&\frac {6}{6+%X_{\mathrm {B}}}\times 22.5 \\[ 5pt ]
6+%X_{\mathrm {B}}&=&\frac {6}{10}\times 22.5 \\[ 5pt ]
%X_{\mathrm {B}}&=&\frac {6}{10}\times 22.5-6 \\[ 5pt ]
&=&7.5 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)この負荷条件における電圧変動率\( \ \mathrm {[%]} \ \)
負荷力率\( \ \cos \theta =0.8 \ \)なので\( \ \sin \theta \ \)は,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.8^{2} } \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,抵抗分は無視できるので,ワンポイント解説「4.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)」の通り,
\[
\begin{eqnarray}
\varepsilon &≃&%X_{\mathrm {B}}\sin \theta +\frac {1}{200}\left( %X_{\mathrm {B}}\cos \theta \right) ^{2} \\[ 5pt ]
&=&7.5\times 0.6 +\frac {1}{200}\left( 7.5\times 0.8 \right) ^{2} \\[ 5pt ]
&=&4.68 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※本問は電圧変動率\( \ 4 \ \mathrm {[%]} \ \)以上なので,上式を用いる必要があります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは