《機械・制御》〈回転機〉[H23:問1]三相かご形誘導電動機のトルクや滑りに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

定格電圧\( \ 200 \ \mathrm {[V]} \ \)，定格周波数\( \ 50 \ \mathrm {[Hz]} \ \)，\( \ 4 \ \)極の三相かご形誘導電動機がある。\( \ \mathrm {L} \ \)形等価回路の一次巻線抵抗\( \ r_{1}=0.1 \ \mathrm {[\Omega ]} \ \)，一次漏れリアクタンス\( \ x_{1}=0.3 \ \mathrm {[\Omega ]} \ \)，二次巻線抵抗の一次側換算値\( \ r_{2}^{\prime }=0.15 \ \mathrm {[\Omega ]} \ \)，二次漏れリアクタンスの一次側換算値\( \ x_{2}^{\prime }=0.4 \ \mathrm {[\Omega ]} \ \)である。誘導電動機を定格電圧，定格周波数の三相交流電源に接続して運転するとき，次の問に答えよ。ただし，励磁電流による電圧降下と鉄損は無視できるものとする。

(1)　滑りが\( \ s=0.05 \ \)のときのトルク\( \ T \ \mathrm {[N\cdot m]} \ \)を求めよ。

(2)　最大トルクが得られる滑り\( \ s_{\mathrm {max}} \ \)を求めよ。

(3)　誘導電動機が同期速度で回転しているものとする。三相交流電源のうち\( \ 2 \ \)線を入れ替えて逆相制動を行うとき，静止するまでの間で制動トルクが最大となる回転速度を求めよ。

(4)　上記(3)で\( \ 2 \ \)線を入れ替えた直後の制動トルクを求めよ。

【ワンポイント解説】

誘導電動機における諸計算に関する問題です。
等価回路を描いて，トルクを導出する等の計算は頻出の内容となるので，確実にマスターしておくようにしましょう。
ただし，本問をまともに解くと比較的時間を要するので，試験本番までに途中で迷うことなく計算できるレベルまで実力を上げておくようにしましょう。

1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。また，同期角速度\( \ \omega _{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] &=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ] &=&\frac {4\pi f}{p} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \)，回転数が\( \ N \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2} \ \)は二次電流，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。

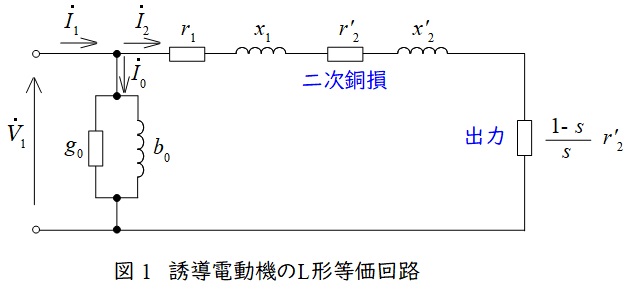
図1より，
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるから，二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ] &=&3\frac {r_{2}^{\prime}}{s}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right) ^{2} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\] となり，発生するトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {(1-s)P_{2}}{(1-s)\omega _{s}} \\[ 5pt ] &=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

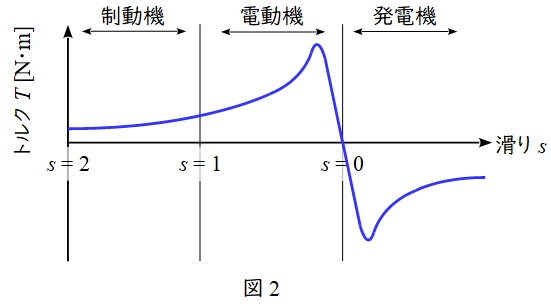
4.誘導電動機のトルク－滑り特性
各滑りのときの誘導電動機の動作は下記の通りとなり，トルク－滑り特性は図2のように整理されます。

①滑りが\( \ s \gt 1 \ \)のとき
同期速度を\( \ N_{\mathrm {s}} \ \)，回転速度を\( \ N \ \)としたとき，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}}&\gt &1 \\[ 5pt ] &&N_{\mathrm {s}}-N&\gt &N_{\mathrm {s}} \\[ 5pt ] &&　　　N&\lt &0 \\[ 5pt ] \end{eqnarray}
\] となり，回転子が磁束の回転方向に対し逆回転している状態となります。したがって，制動機として動作します。

②滑りが\( \ 0 \lt s \lt 1 \ \)のとき
\[
\begin{eqnarray}
0 &\lt & 　　s &\lt & 1 \\[ 5pt ] 0 &\lt & \frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} &\lt & 1 \\[ 5pt ] 0 &\lt & N_{\mathrm {s}}-N &\lt & N_{\mathrm {s}} \\[ 5pt ] -N_{\mathrm {s}} &\lt & 　-N &\lt & 0 \\[ 5pt ] 0 &\lt & 　　N &\lt & N_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] となり，回転速度が磁束の回転速度より小さい値で正回転している状態となります。したがって，電動機として動作します。
③滑りが\( \ s \lt 0 \ \)のとき
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}}&＜ &0 \\[ 5pt ] &&N_{\mathrm {s}}-N&＜ &0 \\[ 5pt ] &&　　　N&＞ &N_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] となり，回転速度が磁束の回転速度より大きい値で正回転している状態となります。したがって，発電機として動作します。

【解答】

(1)滑りが\( \ s=0.05 \ \)のときのトルク\( \ T \ \mathrm {[N\cdot m]} \ \)
ワンポイント解説「3.誘導電動機の\( \ \mathrm {L} \ \)形等価回路」の通り，滑りが\( \ s=0.05 \ \)のときのトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T&=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{\displaystyle \frac {4\pi f}{p}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] &=&\frac {3\times 0.15}{\displaystyle \frac {4\pi \times 50}{4}\times 0.05}\times \frac {\displaystyle \left( \frac {200}{\sqrt {3}}\right) ^{2}}{\displaystyle \left( 0.1+\frac {0.15}{0.05}\right) ^{2} +(0.3+0.4) ^{2}} \\[ 5pt ] &≒&\frac {0.45}{7.8540}\times \frac {40000}{3\times 10.1} \\[ 5pt ] &≒&75.638　→　75.6 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)最大トルクが得られる滑り\( \ s_{\mathrm {max}} \ \)
最大トルクが得られるときは，分母の\( \ \displaystyle A=s\left\{ \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}\right\} \ \)が最小となるときであり，\( \ A \ \)を微分すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}s}&=&1\cdot \left\{ \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}\right\} +s\cdot 2\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) \cdot \left( -\frac {r_{2}^{\prime}}{s^{2}}\right) \\[ 5pt ] &=& \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2} +\left( 2r_{1}s+2r_{2}^{\prime}\right) \cdot \left( -\frac {r_{2}^{\prime}}{s^{2}}\right) \\[ 5pt ] &=&r_{1}^{2}+\frac {2r_{1}r_{2}^{\prime}}{s}+\frac {{r_{2}^{\prime}}^{2}}{s^{2}} +(x_{1}+x_{2}^{\prime}) ^{2} -\frac {2r_{1}r_{2}^{\prime}}{s}-\frac {2{r_{2}^{\prime}}^{2}}{s^{2}} \\[ 5pt ] &=&r_{1}^{2}-\frac {{r_{2}^{\prime}}^{2}}{s^{2}} +(x_{1}+x_{2}^{\prime}) ^{2} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ A \ \)が最小のとき\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}s}=0 \ \)であるから，
\[
\begin{eqnarray}
r_{1}^{2}-\frac {{r_{2}^{\prime}}^{2}}{s^{2}} +(x_{1}+x_{2}^{\prime}) ^{2}&=&0 \\[ 5pt ] \frac {{r_{2}^{\prime}}^{2}}{s^{2}}&=&r_{1}^{2}+(x_{1}+x_{2}^{\prime}) ^{2} \\[ 5pt ] s^{2}&=&\frac {{r_{2}^{\prime}}^{2}}{r_{1}^{2}+(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] s&=&\frac {r_{2}^{\prime}}{\sqrt {r_{1}^{2}+(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，\( \ s_{\mathrm {max}} \ \)は，各値を代入すると，
\[
\begin{eqnarray}
s_{\mathrm {max}}&=&\frac {0.15}{\sqrt {0.1^{2}+(0.3+0.4) ^{2}}} \\[ 5pt ] &≒&0.21213　→　0.212 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)三相交流電源のうち\( \ 2 \ \)線を入れ替えて逆相制動を行うとき，静止するまでの間で制動トルクが最大となる回転速度
逆相制動を行うとき，滑りは\( \ s \gt 1 \ \)となるから，図2より，静止するまでの間で制動となる滑りは，\( \ s=1 \ \)の時であり，回転速度は\( \ N=0 \ \)の時である。

(4)上記(3)で\( \ 2 \ \)線を入れ替えた直後の制動トルク
同期速度で運転しているときに\( \ 2 \ \)線を入れ替えたので，滑りは\( \ s=2 \ \)となる。したがって，そのときのトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T&=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{\displaystyle \frac {4\pi f}{p}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] &=&\frac {3\times 0.15}{\displaystyle \frac {4\pi \times 50}{4}\times 2}\times \frac {\displaystyle \left( \frac {200}{\sqrt {3}}\right) ^{2}}{\displaystyle \left( 0.1+\frac {0.15}{2}\right) ^{2} +(0.3+0.4) ^{2}} \\[ 5pt ] &≒&\frac {0.45}{314.16}\times \frac {40000}{3\times 0.52063} \\[ 5pt ] &≒&36.7 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。