《機械・制御》〈回転機〉[H26:問1]三相かご形誘導電動機の回路計算に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格線間電圧$200 \ \mathrm {V}$，定格周波数$50 \ \mathrm {Hz}$，$4$極の三相かご形誘導電動機について，三相星形結線1相分のL形等価回路から動作特性を考える。三相星形結線1相分のL形等価回路の回路定数を，励磁アドミタンス${\dot y}_{0}=0.05-\mathrm {j}0.15 \ \mathrm {S}$，一次抵抗$r_{1}=0.1 \ \Omega$，一次漏れリアクタンス$x_{1}=0.3 \ \Omega$，二次抵抗の一次側換算値$r_{2}^{\prime}=0.15 \ \Omega$，二次漏れリアクタンスの一次側換算値$x_{2}^{\prime}=0.4 \ \Omega$とする。誘導電動機を定格電圧，定格周波数の三相交流電源に接続し，負荷トルクを$T_{\mathrm {L}} \ \mathrm {[N\cdot m]}$としたとき，滑りは$s=0.03$であった。負荷トルクが$T_{\mathrm {L}} \ \mathrm {[N\cdot m]}$のときの次の値を求めよ。

(1)　同期速度$n_{0} \ \mathrm {[min^{-1}]}$

(2)　励磁電流$I_{0} \ \mathrm {[A]}$

(3)　二次電流の一次換算値$I_{2}^{\prime} \ \mathrm {[A]}$

(4)　負荷トルク$T_{\mathrm {L}} \ \mathrm {[N\cdot m]}$

(5)　一次電流$I_{1} \ \mathrm {[A]}$

(6)　入力力率

【ワンポイント解説】

三相誘導電動機のL形等価回路を描ければ，計算は比較的容易にできると思います。二次試験としては非常に出題されやすい内容で比較的オーソドックスな問題なので，二次試験レベルの受験生であればかなりの方が選択し解けた問題ではないかと思います。

1.電動機の同期速度$N_{\mathrm {s}}$
定格周波数が$f \ \mathrm {[Hz]}$，極数が$p$の電動機の同期速度$N_{\mathrm {s}} \ \mathrm {[min^{-1}]}$は，
$$\begin{eqnarray} N_{\mathrm {s}}&=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}$$ となります。

2.電動機の同期角速度$\omega _{\mathrm {s}}$
同期速度が$N_{\mathrm {s}}$の電動機の同期角速度$\omega _{\mathrm {s}}$は，
$$\begin{eqnarray} \omega _{\mathrm {s}}&=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] \end{eqnarray}$$

3.誘導電動機の出力$P_{\mathrm {o}}$とトルク$T$の関係
電動機の出力$P_{\mathrm {o}}$，角速度$\omega$，電動機の二次入力を$P_{2}$，同期角速度$\omega _{\mathrm {s}}$とすると，電動機のトルク$T$は，
$$\begin{eqnarray} T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {P_{2}\left( 1-s \right) }{\omega _{\mathrm {s}}\left( 1-s \right) } \\[ 5pt ] &=&\frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}$$ で求められます。

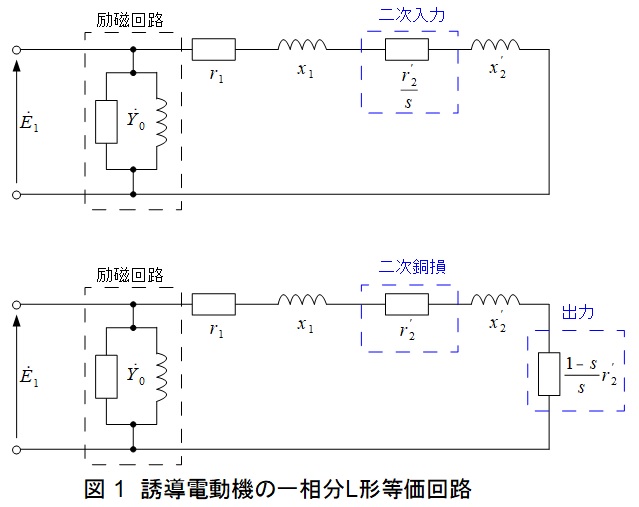
4.誘導電動機のL形等価回路
図1がL形等価回路となります。図1の上下の図はいずれもL形等価回路ですが，下図は入力分$\displaystyle \frac {r^{\prime }_{2}}{s}$を銅損分と出力分に分けたものです。

【解答】

(1)同期速度$n_{0} \ \mathrm {[min^{-1}]}$
ワンポイント解説「1.電動機の同期速度$N_{\mathrm {s}}$」より，同期速度$n_{0} \ \mathrm {[min^{-1}]}$は，
$$\begin{eqnarray} n_{0}&=&\frac {120f}{p} \\[ 5pt ] &=&\frac {120\times 50}{4} \\[ 5pt ] &=&1500 \ \mathrm {[min^{-1}]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(2)励磁電流$I_{0} \ \mathrm {[A]}$
L形等価回路に沿って，励磁電流$I_{0} \ \mathrm {[A]}$を求めると，
$$\begin{eqnarray} {\dot I}_{0}&=&{\dot E}_{0}\cdot {\dot y}_{0} \\[ 5pt ] &=&\frac {200}{\sqrt {3}}\times \left( 0.05-\mathrm {j}0.15 \right) \\[ 5pt ] I_{0}&=&\frac {200}{\sqrt {3}}\times \sqrt {0.05^{2}+0.15^{2}} \\[ 5pt ] &≒&18.257　→　18.3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(3)二次電流の一次換算値$I_{2}^{\prime} \ \mathrm {[A]}$
L形等価回路より，二次側回路の合成インピーダンス$\dot Z$は，
$$\begin{eqnarray} \dot Z&=&r_{1}+\mathrm {j}x_{1}+\frac {r_{2}^{\prime }}{s}+\mathrm {j}x_{2}^{\prime } \\[ 5pt ] &=&0.1+\mathrm {j}0.3+\frac {0.15}{0.03}+\mathrm {j}0.4 \\[ 5pt ] &=&5.1+\mathrm {j}0.7 \\[ 5pt ] \end{eqnarray}$$ であるから，二次電流の一次換算値$I_{2}^{\prime} \ \mathrm {[A]}$の大きさは，
$$\begin{eqnarray} {\dot I}_{2}^{\prime} &=&\frac {{\dot E}_{0}}{\dot Z} \\[ 5pt ] &=&\frac {200}{\sqrt {3}}\cdot \frac {1}{5.1+\mathrm {j}0.7} \\[ 5pt ] I_{2}^{\prime}&=&\frac {200}{\sqrt {3}}\cdot \frac {1}{\sqrt {5.1^{2}+0.7^{2}}} \\[ 5pt ] &≒&22.431　→　22.4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$

(4)負荷トルク$T_{\mathrm {L}} \ \mathrm {[N\cdot m]}$
ワンポイント解説「3.誘導電動機の出力$P_{\mathrm {o}}$とトルク$T$の関係」より，トルクの導出には二次入力$P_{2}$と同期角速度$\omega _{0}$を求めれば良い。二次入力$P_{2}$は，
$$\begin{eqnarray} P_{2} &=&3\cdot \frac {r_{2}^{\prime }}{s}{I_{2}^{\prime}}^{2} \\[ 5pt ] &=&3\times \frac {0.15}{0.03}\times 22.431^{2} \\[ 5pt ] &≒&7547.2 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}$$ となり，同期角速度$\omega _{0}$は，
$$\begin{eqnarray} \omega _{0} &=&\frac {2\pi n_{0}}{60} \\[ 5pt ] &=&\frac {2\pi \times 1500}{60} \\[ 5pt ] &≒&157.08 \ \mathrm {[rad/s]} \\[ 5pt ] \end{eqnarray}$$ となるので，負荷トルク$T_{\mathrm {L}} \ \mathrm {[N\cdot m]}$は，
$$\begin{eqnarray} T_{\mathrm {L}}&=&\frac {P}{\omega } \\[ 5pt ] &=&\frac {P_{2}\left( 1-s \right) }{\omega _{\mathrm {0}}\left( 1-s \right) } \\[ 5pt ] &=&\frac {P_{2}}{\omega _{\mathrm {0}}} \\[ 5pt ] &=&\frac {7547.2}{157.08} \\[ 5pt ] &≒&48.047　→　48.0 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(5)一次電流$I_{1} \ \mathrm {[A]}$
L形等価回路より，
$$\begin{eqnarray} {\dot I}_{1}&=&{\dot I}_{0}+{\dot I}_{2}^{\prime } \\[ 5pt ] &=&\frac {200}{\sqrt {3}}\times \left( 0.05-\mathrm {j}0.15 \right)+\frac {200}{\sqrt {3}}\cdot \frac {1}{5.1+\mathrm {j}0.7} \\[ 5pt ] &≒&27.996-\mathrm {j}20.371 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ となるので，その大きさは，
$$\begin{eqnarray} I_{1}&=&\sqrt {27.996^{2}+20.371^{2}} \\[ 5pt ] &≒&34.623　→　34.6 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(6)入力力率
入力力率は一次電流の大きさとその実部の関係であるから，入力力率$\cos \theta$は，
$$\begin{eqnarray} \cos \theta &=&\frac {27.996}{34.623} \\[ 5pt ] &≒&0.80860　→　0.809 \\[ 5pt ] \end{eqnarray}$$ と求められる。