Contents
【問題】
【難易度】★★★★☆(やや難しい)
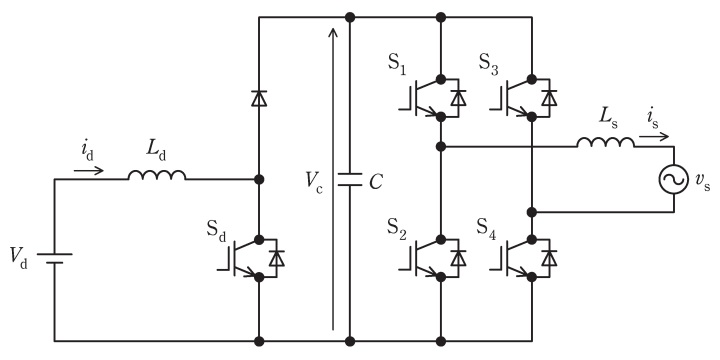
図は太陽光発電用電力変換器の回路図である。入力電圧は\( \ V_{\mathrm {d}}=200 \ \mathrm {V} \ \)で,直流インダクタのインダクタンスは\( \ L_{\mathrm {d}}=1 \ \mathrm {mH} \ \)である。一方,交流系統電圧\( \ v_{\mathrm {s}} \ \)は実効値\( \ V_{\mathrm {s}}=200 \ \mathrm {V} \ \),周波数\( \ 50 \ \mathrm {Hz} \ \)の正弦波電圧で,交流インダクタ\( \ L_{\mathrm {s}} \ \)のリアクタンスは\( \ X_{\mathrm {s}}=3.5 \ \mathrm {\Omega } \ \)である。直流コンデンサ\( \ C \ \)は十分に大きく電圧リプルは無視できる。\( \ \mathrm {S}_{1}~\mathrm {S}_{4} \ \)及び\( \ S_{\mathrm {d}} \ \)のスイッチング周波数は\( \ f_{\mathrm {sw}}=10 \ \mathrm {kHz} \ \)で,スイッチング素子\( \ S_{\mathrm {d}} \ \)のデューティ比は\( \ D=0.5 \ \)一定とする。インバータは,正弦波\( \ \mathrm {PWM} \ \)制御により系統電流\( \ i_{\mathrm {s}} \ \)の基本波成分を\( \ v_{\mathrm {s}} \ \)と同位相に制御するものとする。また,回路素子はすべて理想的とし,損失は生じないものとする。次の問に答えよ。
(1) 出力電力\( \ P_{\mathrm {s}}=4 \ \mathrm {kW} \ \)時の,系統電流\( \ i_{\mathrm {s}} \ \)の基本波実効値\( \ I_{\mathrm {s}} \ \)を求めよ。
(2) 出力電力\( \ P_{\mathrm {s}}=4 \ \mathrm {kW} \ \)時の,交流インダクタ\( \ L_{\mathrm {s}} \ \)に誘起する電圧の基本波実効値,及びインバータ交流端子電圧の基本波実効値を求めよ。
(3) 出力電力\( \ P_{\mathrm {s}}=4 \ \mathrm {kW} \ \)時に\( \ i_{\mathrm {s}} \ \)を制御するために必要な直流コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm {c}} \ \)の条件を示せ。
(4) 昇圧コンバータが電流連続モードで動作した場合,すなわち入力電流が常に\( \ i_{\mathrm {d}}>0 \ \)の場合のコンデンサ電圧\( \ V_{\mathrm {c}} \ \)を求めよ。
(5) 電流連続モードの場合,\( \ i_{\mathrm {d}} \ \)のリプルのピークピーク値を求めよ。
(6) 電流連続モードで動作できる出力電力\( \ P_{\mathrm {s}} \ \)の条件を示せ。
【ワンポイント解説】
太陽光発電のパワーコンディショナのメカニズムを問うような出題です。令和元年度の機械制御の科目は比較的取り組みやすい問題が多かった印象ですが,本問だけは少し難易度が高めの問題となっています。選択する必要のない方は飛ばしても良いかもしれません。
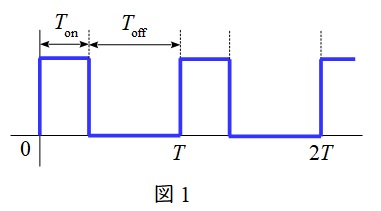
1.デューティ比\( \ D \ \)
周期が\( \ T \ \)の図1のような方形波において,デューティ比\( \ D \ \)は,
\[
\begin{eqnarray}
D&=&\frac {T_{\mathrm {on}}}{T} \\[ 5pt ]
&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)系統電流\( \ i_{\mathrm {s}} \ \)の基本波実効値\( \ I_{\mathrm {s}} \ \)
この回路の出力は単相交流なので,
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&V_{\mathrm {s}}I_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,それぞれの値を代入すると,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {P_{\mathrm {s}}}{V_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {4\times 10^{3}}{200} \\[ 5pt ]
&=&20.0 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)交流インダクタ\( \ L_{\mathrm {s}} \ \)に誘起する電圧の基本波実効値,及びインバータ交流端子電圧の基本波実効値
交流インダクタ\( \ L_{\mathrm {s}} \ \)に誘起する電圧の基本波実効値\( \ V_{\mathrm {ls}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {ls}}&=&X_{\mathrm {s}}I_{\mathrm {s}} \\[ 5pt ]
&=&3.5\times 20 \\[ 5pt ]
&=&70.0 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。インバータの交流端子電圧\( \ {\dot V}_{\mathrm {i}} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {i}}&=&{\dot V}_{\mathrm {s}}+\mathrm {j}X_{\mathrm {s}}I_{\mathrm {s}} \\[ 5pt ]
&=&200+\mathrm {j}70.0 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,その大きさ\( \ V_{\mathrm {i}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {i}}&=&\sqrt {200^{2}+70.0^{2}} \\[ 5pt ]
&≒&211.90 → 212 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ i_{\mathrm {s}} \ \)を制御するために必要な直流コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm {c}} \ \)の条件
\( \ V_{\mathrm {c}} \ \)はインバータ電圧の波高値より大きくなければならないので,その条件は,
\[
\begin{eqnarray}
V_{\mathrm {c}}&≧&\sqrt {2}V_{\mathrm {i}} \\[ 5pt ]
&=&\sqrt {2}\times 211.90 \\[ 5pt ]
&≒&299.67 → 300 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)入力電流が常に\( \ i_{\mathrm {d}}>0 \ \)の場合のコンデンサ電圧\( \ V_{\mathrm {c}} \ \)
リアクトル\( \ L_{\mathrm {d}} \ \)に蓄えられるエネルギーについて,
\[
\begin{eqnarray}
V_{\mathrm {d}}I_{\mathrm {d}}T_{\mathrm {on}}&=&\left( V_{\mathrm {c}}-V_{\mathrm {d}}\right) I_{\mathrm {d}}T_{\mathrm {off}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,
\[
\begin{eqnarray}
V_{\mathrm {d}}T_{\mathrm {on}}&=&\left( V_{\mathrm {c}}-V_{\mathrm {d}}\right) T_{\mathrm {off}} \\[ 5pt ]
V_{\mathrm {d}}T_{\mathrm {on}}&=&V_{\mathrm {c}}T_{\mathrm {off}}-V_{\mathrm {d}}T_{\mathrm {off}} \\[ 5pt ]
V_{\mathrm {d}}\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) &=&V_{\mathrm {c}}T_{\mathrm {off}} \\[ 5pt ]
V_{\mathrm {c}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V_{\mathrm {d}} \\[ 5pt ]
&=&\frac {1}{\displaystyle \frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}V_{\mathrm {d}} \\[ 5pt ]
&=&\frac {1}{\displaystyle 1-\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}V_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,デューティ比\( \ \displaystyle D=\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}=0.5 \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {c}}&=&\frac {1}{\displaystyle 1-D}V_{\mathrm {d}} \\[ 5pt ]
&=&\frac {1}{ 1-0.5}\times 200 \\[ 5pt ]
&=&400 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)電流連続モードの場合,\( \ i_{\mathrm {d}} \ \)のリプルのピークピーク値
スイッチング周波数が\( \ f_{\mathrm {sw}}=10 \ \mathrm {kHz} \ \)であるので,スイッチングの周期\( \ T \ \)は,
\[
\begin{eqnarray}
T&=&\frac {1}{f_{\mathrm {sw}}} \\[ 5pt ]
&=&\frac {1}{10\times 10^{3}} \\[ 5pt ]
&=&1\times 10^{-4} \ \mathrm {[s]} \\[ 5pt ]
\end{eqnarray}
\]
となる。デューティ比が\( \ D=0.5 \ \)であるので\( \ T_{\mathrm {on}} \ \)は,
\[
\begin{eqnarray}
T_{\mathrm {on}}&=&DT \\[ 5pt ]
&=&0.5\times 1\times 10^{-4} \\[ 5pt ]
&=&5\times 10^{-5} \ \mathrm {[s]} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \mathrm {S}_{\mathrm {d}} \ \)が\( \ \mathrm {ON} \ \)の時,
\[
\begin{eqnarray}
V_{\mathrm {d}}&=&L_{\mathrm {d}}\frac {\mathrm {d} i}{\mathrm {d} t} \\[ 5pt ]
\end{eqnarray}
\]
が成立するので,リプル電流のピークピーク値は,
\[
\begin{eqnarray}
\frac {\mathrm {d} i}{\mathrm {d} t}T_{\mathrm {on}}&=&\frac {V_{\mathrm {d}}}{L_{\mathrm {d}}}T_{\mathrm {on}} \\[ 5pt ]
&=&\frac {200}{1\times 10^{-3}}\times 5\times 10^{-5} \\[ 5pt ]
&=&10 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)電流連続モードで動作できる出力電力\( \ P_{\mathrm {s}} \ \)の条件
リプル電流のピークピーク値が\( \ 10 \ \mathrm {[A]} \ \)であるので,\( \ i_{\mathrm {d}} \ \)の平均値\( \ I_{\mathrm {d}} \ \)が\( \ 5 \ \mathrm {[A]} \ \)以上でなければ電流連続モードで動作しない。したがって,その時の入力電力\( \ P_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {d}}&=&V_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ]
&=&200\times 5 \\[ 5pt ]
&=&1000 \ \mathrm {[W]} → 1 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,回路素子はすべて理想的とし,損失は生じないので出力電力\( \ P_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&P_{\mathrm {d}} \\[ 5pt ]
&=&1 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,連続モードで動作できる出力電力は\( \ 1 \ \mathrm {kW} \ \)以上と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは