【問題】
【難易度】★★★★☆(やや難しい)
三相星形結線の円筒形同期発電機[定格容量\(100 \ 000 \ \mathrm {kV\cdot A}\),定格電圧(線間電圧)\(V_{\mathrm {R}}=13 \ 800 \ \mathrm {V}\),定格電流(相電流)\(I_{\mathrm {R}}=4 \ 184 \ \mathrm {A}\),定格周波数\(60 \ \mathrm {Hz}\),定格力率\(0.9\)(遅れ)]における正相及び逆相リアクタンスの測定法に関して,次の問に答えよ。ただし,電機子抵抗などの抵抗分は無視する。
(1) 正相リアクタンス
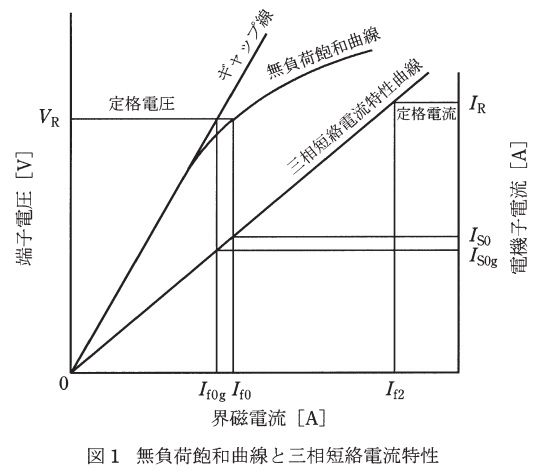
円筒形同期電動機の正相リアクタンスは,定格回転速度で定常運転状態では同期リアクタンスとなる。同期リアクタンスは,図1に示す無負荷飽和曲線と三相短絡電流特性曲線から求めることができる。同期リアクタンスの定格電圧での飽和値\(X_{\mathrm {ss}} \ \mathrm {[\Omega ]}\)及び同期リアクタンスの不飽和値\(X_{\mathrm {su}} \ \mathrm {[\Omega ]}\)を,\(V_{\mathrm {R}}\ \mathrm {[V]}\),\(I_{\mathrm {R}}\ \mathrm {[A]}\),\(I_{\mathrm {f2}}\ \mathrm {[A]}\),\(I_{\mathrm {f0}}\ \mathrm {[A]}\)又は\(I_{\mathrm {f0g}}\ \mathrm {[A]}\)を用いて表す式を導出せよ。その導出過程も示すこと。なお,\(I_{\mathrm {f2}}\),\(I_{\mathrm {f0}}\)及び\(I_{\mathrm {f0g}}\)は図1に示す界磁電流である。また,\(I_{\mathrm {f2}}=600 \ \mathrm {A}\),\(I_{\mathrm {f0}}=300 \ \mathrm {A}\),\(I_{\mathrm {f0g}}=270 \ \mathrm {A}\)として,\(X_{\mathrm {ss}} \ \mathrm {[\Omega ]}\)及び\(X_{\mathrm {su}} \ \mathrm {[\Omega ]}\)を算出せよ。
(2) 逆相リアクタンス
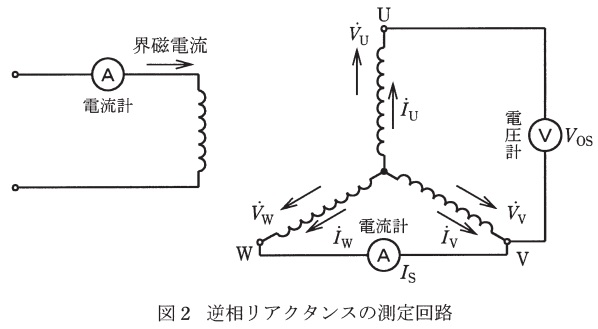
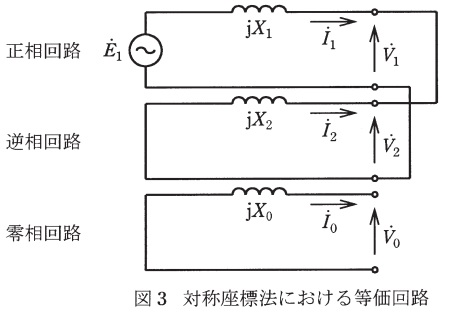
図2に示すように,電機子巻線の2端子を短絡し,発電機を定格回転速度で運転する。界磁電流を流し,短絡回路の電流\(I_{\mathrm {S}}\ \mathrm {[A]}\)及び短絡回路と開放端子との間の電圧\(V_{\mathrm {OS}}\ \mathrm {[V]}\)を計測する。また,このときの対称座標法による等価回路を図3に示す。逆相リアクタンス\(X_{2} \ \mathrm {[\Omega ]}\)を,\(V_{\mathrm {OS}}\ \mathrm {[V]}\)及び\(I_{\mathrm {S}}\ \mathrm {[A]}\)を用いて表す式を導出せよ。その導出過程も示すこと。また,\(V_{\mathrm {OS}}=250 \ \mathrm {V}\),\(I_{\mathrm {S}}=400 \ \mathrm {A}\)として,\(X_{\mathrm {2}} \ \mathrm {[\Omega ]}\)を算出せよ。
【ワンポイント解説】
二種では出題頻度のあまり高くない対称座標法を用いたり,測定の原理を求めたりする難問と言えると思います。対称座標法は慣れてしまえば比較的簡単に解くことができるので,本問を通じて理解しておくようにしておきましょう。
1.電動機の特性曲線
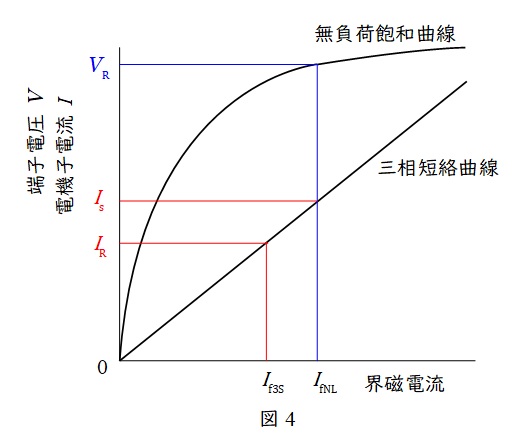
電動機は図4のような無負荷飽和特性と三相短絡電流特性があります。直軸同期リアクタンス\(X_{\mathrm {d}}\)は図4の\(\displaystyle \frac {V_{\mathrm {R}} / \sqrt{3}}{I_{\mathrm {s}}}\)で求められます。
2.対称座標法
零相電圧\({\dot V}_{0}\),正相電圧\({\dot V}_{1}\),逆相電圧\({\dot V}_{2}\)とすると,各相の電圧\({\dot V}_{\mathrm {U}}\),\({\dot V}_{\mathrm {V}}\),\({\dot V}_{\mathrm {W}}\)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {U}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {V}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {W}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2}
\end{eqnarray}
\]
零相電流\({\dot I}_{0}\),正相電流\({\dot I}_{1}\),逆相電流\({\dot I}_{2}\)とすると,各相の電流\({\dot I}_{\mathrm {U}}\),\({\dot I}_{\mathrm {V}}\),\({\dot I}_{\mathrm {W}}\)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {U}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {V}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {W}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2}
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)正相リアクタンス
ワンポイント解説「1.電動機の特性曲線」より,同期リアクタンスの定格電圧での飽和値\(X_{\mathrm {ss}}\)は,
\[
\begin{eqnarray}
X_{\mathrm {ss}} &=&\frac {V_{\mathrm {R}} / \sqrt{3}}{I_{\mathrm {S0}}} ・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。図1の三相短絡電流特性曲線より,
\[
\begin{eqnarray}
\frac {I_{\mathrm {f2}}}{I_{\mathrm {f0}}} &=&\frac {I_{\mathrm {R}}}{I_{\mathrm {S0}}} \\[ 5pt ]
I_{\mathrm {S0}} &=&\frac {I_{\mathrm {f0}}}{I_{\mathrm {f2}}}\cdot I_{\mathrm {R}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを①に代入すると,
\[
\begin{eqnarray}
X_{\mathrm {ss}} &=&\frac {V_{\mathrm {R}} / \sqrt{3}}{I_{\mathrm {S0}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {R}} / \sqrt{3}}{\frac {I_{\mathrm {f0}}}{I_{\mathrm {f2}}}\cdot I_{\mathrm {R}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {R}}I_{\mathrm {f2}}}{\sqrt{3}I_{\mathrm {R}}I_{\mathrm {f0}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。同様に同期リアクタンスの定格電圧での不飽和値\(X_{\mathrm {su}}\)は,\(I_{\mathrm {f0}}→I_{\mathrm {f0g}}\)とすれば良いので,
\[
\begin{eqnarray}
X_{\mathrm {su}} &=&\frac {V_{\mathrm {R}}I_{\mathrm {f2}}}{\sqrt{3}I_{\mathrm {R}}I_{\mathrm {f0g}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。題意に沿って,各値を代入すると,
\[
\begin{eqnarray}
X_{\mathrm {ss}} &=&\frac {V_{\mathrm {R}}I_{\mathrm {f2}}}{\sqrt{3}I_{\mathrm {R}}I_{\mathrm {f0}}} \\[ 5pt ]
&=&\frac {13800\times 600}{\sqrt{3}\times 4184 \times 300} \\[ 5pt ]
&≒&3.8085 → 3.81 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
X_{\mathrm {su}} &=&\frac {V_{\mathrm {R}}I_{\mathrm {f2}}}{\sqrt{3}I_{\mathrm {R}}I_{\mathrm {f0g}}} \\[ 5pt ]
&=&\frac {13800\times 600}{\sqrt{3}\times 4184 \times 270} \\[ 5pt ]
&≒&4.2317 → 4.23 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)逆相リアクタンス
図3より,
\[
\begin{eqnarray}
{\dot V}_{0} &=&0 &・・・・・②& \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{1}-\mathrm {j}X_{1}{\dot I}_{1} &・・・・・③& \\[ 5pt ]
{\dot V}_{2} &=& -\mathrm {j}X_{2}{\dot I}_{2} = {\dot V}_{1} &・・・・・④& \\[ 5pt ]
{\dot I}_{0} &=&0 &・・・・・⑤& \\[ 5pt ]
{\dot I}_{1} &=&\frac {{\dot E}_{1}}{\mathrm {j}X_{1}+\mathrm {j}X_{2}}=-{\dot I}_{2} &・・・・・⑥& \\[ 5pt ]
\end{eqnarray}
\]
となる。④に⑥を代入すると,
\[
\begin{eqnarray}
{\dot V}_{1}={\dot V}_{2} &=& -\mathrm {j}X_{2}{\dot I}_{2} \\[ 5pt ]
&=& \frac {\mathrm {j}X_{2}{\dot E}_{1}}{\mathrm {j}X_{1}+\mathrm {j}X_{2}} \\[ 5pt ]
&=& \frac {X_{2}{\dot E}_{1}}{X_{1}+X_{2}} ・・・・・⑦ \\[ 5pt ]
\end{eqnarray}
\]
図2及びワンポイント解説「2.対称座標法」より,電圧計の測定電圧\({\dot V}_{\mathrm {OS}}\)は,\(1+a+a^{2}=0\)を用いて整理すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {OS}} &=& {\dot V}_{\mathrm {U}}-{\dot V}_{\mathrm {V}} \\[ 5pt ]
&=& {\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2}- \left( {\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2}\right) \\[ 5pt ]
&=& \left( 1-a^{2}\right) {\dot V}_{1} + \left( 1-a\right) {\dot V}_{2} \\[ 5pt ]
&=& \left( 2-a-a^{2}\right) {\dot V}_{1} \\[ 5pt ]
&=& 3 {\dot V}_{1} \\[ 5pt ]
&=& \frac {3X_{2}{\dot E}_{1}}{X_{1}+X_{2}} ・・・・・⑧ \\[ 5pt ]
\end{eqnarray}
\]
となる。一方電流計の測定電流\({\dot I}_{\mathrm {S}}\)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {S}} &=& {\dot I}_{\mathrm {V}} \\[ 5pt ]
&=& {\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
&=& a^{2}{\dot I}_{1} – a{\dot I}_{1} \\[ 5pt ]
&=& \left( a^{2}-a\right) {\dot I}_{1} \\[ 5pt ]
&=& \left( \frac {-1-\mathrm {j}\sqrt {3}}{2}-\frac {-1+\mathrm {j}\sqrt {3}}{2}\right) {\dot I}_{1} \\[ 5pt ]
&=& -\mathrm {j}\sqrt {3}{\dot I}_{1} \\[ 5pt ]
&=& -\mathrm {j}\sqrt {3}\frac {{\dot E}_{1}}{\mathrm {j}X_{1}+\mathrm {j}X_{2}} \\[ 5pt ]
&=& -\sqrt {3}\frac {{\dot E}_{1}}{X_{1}+X_{2}} ・・・・・⑨ \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\(\left| ⑧\right| ÷\left| ⑨\right| \)により,
\[
\begin{eqnarray}
\frac {\left| {\dot V}_{\mathrm {OS}}\right| }{\left| {\dot I}_{\mathrm {S}}\right| } &=& \frac {\frac {3X_{2}\left| {\dot E}_{1}\right| }{X_{1}+X_{2}}}{\sqrt {3}\frac {\left| {\dot E}_{1}\right| }{X_{1}+X_{2}} } \\[ 5pt ]
&=& \sqrt {3}X_{2} \\[ 5pt ]
X_{2}&=& \frac {\left| {\dot V}_{\mathrm {OS}}\right| }{\sqrt {3}\left| {\dot I}_{\mathrm {S}}\right| }\\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,各値を代入すると,
\[
\begin{eqnarray}
X_{2}&=& \frac {\left| {\dot V}_{\mathrm {OS}}\right| }{\sqrt {3}\left| {\dot I}_{\mathrm {S}}\right| }\\[ 5pt ]
&=& \frac {250}{\sqrt {3}\times 400}\\[ 5pt ]
&≒&0.36084 → 0.361 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは