Contents
【問題】
【難易度】★★★☆☆(普通)
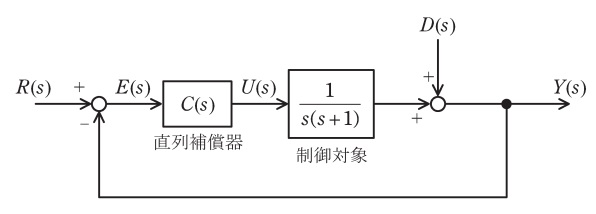
図のようなフィードバック制御系について,次の問に答えよ。ただし,\( \ R\left( s\right) \ \)は目標値,\( \ D\left( s\right) \ \)は外乱,\( \ U\left( s\right) \ \)は操作量,\( \ Y\left( s\right) \ \)は制御量,\( \ E\left( s\right) \ \)は偏差とする。外乱\( \ D\left( s\right) \ \)の時間関数は次に示すランプ関数であり,\( \ \displaystyle \begin{eqnarray}
d\left( t\right)
=
\begin{cases}
\displaystyle 2t & ( t ≧ 0 ) \\
\displaystyle 0 & ( t < 0 )
\end{cases}
\end{eqnarray} \ \)とする。
(1) \( \ R\left( s\right) =0\ \),\( \ C\left( s\right) =K>0 \ \)のとき,外乱\( \ D\left( s\right) \ \)による定常速度偏差\( \ e_{\mathrm {v}} \ \)を求めよ。
(2) \( \ C\left( s\right) =K>0 \ \)のとき,閉ループ系の安定性の指標の一つである減衰係数\( \ \zeta \ \)を\( \ 0.8 \ \)に設定するための\( \ K \ \)の値を求めよ。
(3) \( \ R\left( s\right) =0\ \),\( \ \displaystyle C\left( s\right) =A\cdot \frac {s+1}{0.1s+1}\left( A>0 \right) \ \)の場合について,外乱\( \ D\left( s\right) \ \)による定常速度偏差\( \ e_{\mathrm {v}} \ \)を求めよ。
(4) 上記(3)の\( \ C\left( s\right) \ \)を用いた閉ループ系の減衰定数\( \ \zeta \ \)が\( \ 0.8 \ \)になるような\( \ A \ \)の値を求めよ。
(5) 上記(2)と上記(4)の場合,それぞれにおいて閉ループ系の固有角周波数\( \ \omega _{\mathrm {n}} \ \)を求めよ。その結果,上記(2)の場合に比べて上記(4)の場合は,応答が何倍になるかを示せ。
(6) 上記(2)と上記(4)の場合,それぞれにおいて外乱\( \ D\left( s\right) \ \)に対する定常速度偏差\( \ e_{\mathrm {v}} \ \)を求めよ。その結果,上記(2)の場合に比べて上記(4)の場合は,定常速度偏差が何倍になるかを示せ。
【ワンポイント解説】
フィードバック制御系からの定常速度偏差の比較に関する問題です。
少し問題量が多くラプラス変換や最終値の定理,減衰定数\( \ \zeta \ \)や固有角周波数\( \ \omega _{\mathrm {n}} \ \)等覚える必要がある内容が多いですが,いずれも過去問で出題されているので,きちんと過去問を習得していれば完答も目指せる問題と言えると思います。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
a & \displaystyle \frac {a}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\hline
\end{array}
\]
2.定常偏差(最終値の定理)
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常偏差は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
3.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)
2次遅れの伝達関数\( \ W(s) \ \)の一般式は,減衰係数\( \ \zeta \ \),固有角周波数\( \ \omega _{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
W(s)&=&\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表されます。
【解答】
(1)\( \ R\left( s\right) =0\ \),\( \ C\left( s\right) =K>0 \ \)のとき,外乱\( \ D\left( s\right) \ \)による定常速度偏差\( \ e_{\mathrm {v}} \ \)
問題図のフィードバック制御系において,
\[
\begin{eqnarray}
R\left( s\right) -Y\left( s\right) &=&E\left( s\right) &・・・・・・ ①& \\[ 5pt ]
E\left( s\right) C\left( s\right) &=&U\left( s\right) &・・・・・・ ②& \\[ 5pt ]
U\left( s\right) \cdot \frac {1}{s\left( s+1\right) }+D\left( s\right) &=&Y\left( s\right) &・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,③に②を代入すると,
\[
\begin{eqnarray}
E\left( s\right) C\left( s\right) \cdot \frac {1}{s\left( s+1\right) }+D\left( s\right) &=&Y\left( s\right) ・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに①より\( \ R\left( s\right) -E\left( s\right) =Y\left( s\right) \ \)の関係があるので,これを代入すると,
\[
\begin{eqnarray}
E\left( s\right) C\left( s\right) \cdot \frac {1}{s\left( s+1\right) }+D\left( s\right) &=&R\left( s\right) -E\left( s\right) \\[ 5pt ]
\left\{\frac {C\left( s\right)}{s \left( s+1\right) }+1\right\} E\left( s\right) &=&-D\left( s\right) +R\left( s\right) \\[ 5pt ]
\left\{\frac {s^{2}+s+C\left( s\right)}{s^{2}+s}\right\} E\left( s\right) &=&-D\left( s\right) +R\left( s\right) \\[ 5pt ]
E\left( s\right) &=&\frac {s^{2}+s}{s^{2}+s+C\left( s\right)}\left\{ -D\left( s\right) +R\left( s\right) \right\} ・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ R\left( s\right) =0\ \),\( \ C\left( s\right) =K \ \)を代入すると,
\[
\begin{eqnarray}
E\left( s\right) &=&-\frac {s^{2}+s}{s^{2}+s+K}D\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,ワンポイント解説「1.基本的なラプラス変換」の通り,\( \ t≧0 \ \)のとき,
\[
\begin{eqnarray}
d\left( t\right) =2t ⇔ D\left( s\right) =\frac {2}{s^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,定常速度偏差\( \ e_{\mathrm {v}} \ \)は,ワンポイント解説「2.定常偏差(最終値の定理)」より,
\[
\begin{eqnarray}
e_{\mathrm {v}} &=&\displaystyle \lim _{ t \to \infty } e\left( t\right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } sE\left( s\right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left[ s\cdot \left( -\frac {s^{2}+s}{s^{2}+s+K}\right) \cdot \frac {2}{s^{2}}\right] \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left[ -\frac {2\left( s+1\right) }{s^{2}+s+K}\right] \\[ 5pt ]
&=&-\frac {2}{K} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ C\left( s\right) =K>0 \ \)のとき,閉ループ系の安定性の指標の一つである減衰係数\( \ \zeta \ \)を\( \ 0.8 \ \)に設定するための\( \ K \ \)の値
④に①を代入して整理し,\( \ R\left( s\right) \ \)から\( \ Y\left( s\right) \ \)までの伝達関数を求めると,
\[
\begin{eqnarray}
\left\{ R\left( s\right) -Y\left( s\right) \right\} C\left( s\right) \cdot \frac {1}{s\left( s+1\right) }+D\left( s\right) &=&Y\left( s\right) \\[ 5pt ]
\left\{ R\left( s\right) -Y\left( s\right) \right\} C\left( s\right) +s\left( s+1\right) D\left( s\right) &=&s\left( s+1\right) Y\left( s\right) \\[ 5pt ]
C\left( s\right) R\left( s\right) +\left( s^{2}+s\right) D\left( s\right) &=&\left\{ s^{2}+s+C\left( s\right)\right\} Y\left( s\right) \\[ 5pt ]
Y\left( s\right) &=&\frac {C\left( s\right) }{s^{2}+s+C\left( s\right)}R\left( s\right) +\frac {s^{2}+s}{s^{2}+s+C\left( s\right)}D\left( s\right) ・・・・・・ ⑥ \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ C\left( s\right) =K \ \)を代入すると,
\[
\begin{eqnarray}
Y\left( s\right) &=&\frac {K}{s^{2}+s+K}R\left( s\right) +\frac {s^{2}+s}{s^{2}+s+K}D\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。第1項についてワンポイント解説「3.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)」の標準形\( \ \displaystyle \frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \ \)と比較すると,
\[
\begin{eqnarray}
\omega _{\mathrm {n}}^{2} &=&K \\[ 5pt ]
2\zeta \omega _{\mathrm {n}} &=&1 \\[ 5pt ]
\end{eqnarray}
\]
となるから,
\[
\begin{eqnarray}
\omega _{\mathrm {n}} &=&\sqrt {K} \\[ 5pt ]
\zeta &=&\frac {1}{2\omega _{\mathrm {n}}} \\[ 5pt ]
&=&\frac {1}{2\sqrt {K}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \zeta =0.8 \ \)を代入すると,
\[
\begin{eqnarray}
0.8 &=&\frac {1}{2\sqrt {K}} \\[ 5pt ]
\sqrt {K} &=&0.625 \\[ 5pt ]
K&≒&0.39063 → 0.391 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ R\left( s\right) =0\ \),\( \ \displaystyle C\left( s\right) =A\cdot \frac {s+1}{0.1s+1}\left( A>0 \right) \ \)のとき,外乱\( \ D\left( s\right) \ \)による定常速度偏差\( \ e_{\mathrm {v}} \ \)
⑤に\( \ R\left( s\right) =0\ \),\( \ \displaystyle C\left( s\right) =A\cdot \frac {s+1}{0.1s+1} \ \)を代入すると,
\[
\begin{eqnarray}
E\left( s\right) &=&\frac {s^{2}+s}{s^{2}+s+C\left( s\right)}\left\{ -D\left( s\right) +R\left( s\right) \right\} \\[ 5pt ]
&=&-\frac {s^{2}+s}{s^{2}+s+A\cdot \displaystyle \frac {s+1}{0.1s+1}}D\left( s\right) \\[ 5pt ]
&=&-\frac {s\left( s+1\right) }{s\left( s+1\right) +A\cdot \displaystyle \frac {s+1}{0.1s+1}}D\left( s\right) \\[ 5pt ]
&=&-\frac {s}{s+A\cdot \displaystyle \frac {1}{0.1s+1}}D\left( s\right) \\[ 5pt ]
&=&-\frac {s}{\displaystyle \frac {\left( 0.1s+1\right) s+A}{0.1s+1}}D\left( s\right) \\[ 5pt ]
&=&-\frac {0.1s^{2}+s}{0.1s^{2}+s+A}D\left( s\right) \\[ 5pt ]
&=&-\frac {s^{2}+10s}{s^{2}+10s+10A}D\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,(1)と同様に\( \ \displaystyle D\left( s\right) =\frac {2}{s^{2}} \ \)を代入して,定常速度偏差\( \ e_{\mathrm {v}} \ \)を求めると,
\[
\begin{eqnarray}
e_{\mathrm {v}} &=&\displaystyle \lim _{ t \to \infty } e\left( t\right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } sE\left( s\right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left[ s\cdot \left( -\frac {s^{2}+10s}{s^{2}+10s+10A}\right) \cdot \frac {2}{s^{2}}\right] \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left[ -\frac {2\left( s+10\right) }{s^{2}+10s+10A}\right] \\[ 5pt ]
&=&-\frac {2}{A} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)(3)の\( \ C\left( s\right) \ \)を用いた閉ループ系の減衰定数\( \ \zeta \ \)が\( \ 0.8 \ \)になるような\( \ A \ \)の値
⑥に\( \ \displaystyle C\left( s\right) =A\cdot \frac {s+1}{0.1s+1} \ \)を代入して整理すると,
\[
\begin{eqnarray}
Y\left( s\right) &=&\frac {C\left( s\right) }{s^{2}+s+C\left( s\right)}R\left( s\right) +\frac {s^{2}+s}{s^{2}+s+C\left( s\right)}D\left( s\right) \\[ 5pt ]
&=&\frac {\displaystyle A\cdot \frac {s+1}{0.1s+1}}{\displaystyle s^{2}+s+A\cdot \frac {s+1}{0.1s+1}}R\left( s\right) +\frac {s^{2}+s}{\displaystyle s^{2}+s+A\cdot \frac {s+1}{0.1s+1}}D\left( s\right) \\[ 5pt ]
&=&\frac {\displaystyle \frac {A}{0.1s+1}}{\displaystyle s+\frac {A}{0.1s+1}}R\left( s\right) +\frac {s}{\displaystyle s+\frac {A}{0.1s+1}}D\left( s\right) \\[ 5pt ]
&=&\frac {A}{\displaystyle 0.1s^{2}+s+A}R\left( s\right) +\frac {0.1s^{2}+s}{0.1s^{2}+s+A}D\left( s\right) \\[ 5pt ]
&=&\frac {10A}{\displaystyle s^{2}+10s+10A}R\left( s\right) +\frac {s^{2}+10s}{s^{2}+10s+10A}D\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,第1項についてワンポイント解説「3.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)」の標準形\( \ \displaystyle \frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \ \)と比較すると,
\[
\begin{eqnarray}
\omega _{\mathrm {n}}^{2} &=&10A \\[ 5pt ]
2\zeta \omega _{\mathrm {n}} &=&10 \\[ 5pt ]
\end{eqnarray}
\]
となるから,
\[
\begin{eqnarray}
\omega _{\mathrm {n}} &=&\sqrt {10A} \\[ 5pt ]
\zeta &=&\frac {10}{2\omega _{\mathrm {n}}} \\[ 5pt ]
&=&\frac {5}{\sqrt {10A}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \zeta =0.8 \ \)を代入すると,
\[
\begin{eqnarray}
0.8 &=&\frac {5}{\sqrt {10A}} \\[ 5pt ]
\sqrt {10A} &=&6.25 \\[ 5pt ]
10A&≒&39.063 \\[ 5pt ]
A&≒&3.9063 → 3.91 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)上記(2)と上記(4)の場合,それぞれにおいて閉ループ系の固有角周波数\( \ \omega _{\mathrm {n}} \ \)とその比較
(2)のときの固有角周波数\( \ \omega _{\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {n}} &=&\sqrt {K} \\[ 5pt ]
&=&\sqrt {0.39063} \\[ 5pt ]
&≒&0.62500 \\[ 5pt ]
\end{eqnarray}
\]
であり,(4)のときの固有角周波数\( \ \omega _{\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {n}} &=&\sqrt {10A} \\[ 5pt ]
&=&\sqrt {10\times 3.9063} \\[ 5pt ]
&≒&6.2500 \\[ 5pt ]
\end{eqnarray}
\]
となるので,(4)の方が応答が\( \ 10 \ \)倍速くなる。
(6)上記(2)と上記(4)の場合,それぞれにおいて外乱\( \ D\left( s\right) \ \)に対する定常速度偏差\( \ e_{\mathrm {v}} \ \)とその比較
(2)のときの定常速度偏差\( \ e_{\mathrm {v}} \ \)は,
\[
\begin{eqnarray}
e_{\mathrm {v}} &=&-\frac {2}{K} \\[ 5pt ]
&=&-\frac {2}{0.39063} \\[ 5pt ]
&≒&-5.1199 → -5.12 \\[ 5pt ]
\end{eqnarray}
\]
となり,(4)のときの定常速度偏差\( \ e_{\mathrm {v}} \ \)は,
\[
\begin{eqnarray}
e_{\mathrm {v}} &=&-\frac {2}{A} \\[ 5pt ]
&=&-\frac {2}{3.9063} \\[ 5pt ]
&≒&-0.51199 → -0.512 \\[ 5pt ]
\end{eqnarray}
\]
となるので,(4)の方が定常速度偏差は\( \ \displaystyle \frac {1}{10} \ \)倍となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは