【問題】
【難易度】★★★★★(難しい)
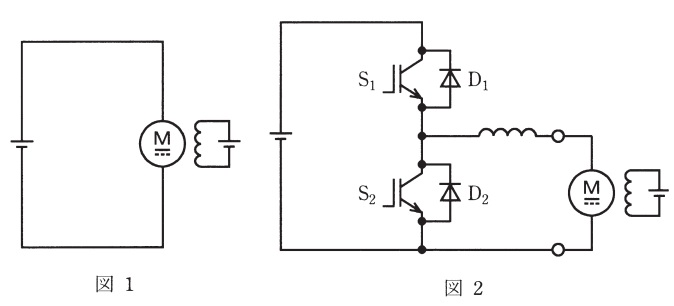
図1のように,他励直流電動機を\( \ 200 \ \mathrm {[V]} \ \)の直流電源に接続し,定格トルクを課したところ,軸出力は\( \ 3.75 \ \mathrm {[kW]} \ \)で,回転速度は\( \ 1 \ 500 \ \mathrm {[{min}^{-1}]} \ \),電機子電流は\( \ 20 \ \mathrm {[A]} \ \),正負ブラシの全電圧降下は\( \ 2.5 \ \mathrm {[V]} \ \)であった。ただし,電動機の許容最高回転速度は十分に高く,界磁電流は一定とし,鉄損,界磁損及び機械損は無視できるものとする。
この電動機を図2のように可逆チョッパに接続した。可逆チョッパの直流入力電圧は\( \ 200 \ \mathrm {[V]} \ \)であり,\( \ \mathrm {IGBT} \ \)の電圧降下は\( \ 2 \ \mathrm {[V]} \ \),逆並列ダイオードの電圧降下は\( \ 1 \ \mathrm {[V]} \ \)とする。ただし,スイッチング損失,平滑リアクトルの抵抗及び出力電流リプルは無視できるものとする。次の値を求めよ。
(1) 電機子巻線抵抗\( \ \mathrm {[\Omega ]} \ \)
(2) 定格トルクと課し,回転速度が\( \ 1 \ 500 \ \mathrm {[{min}^{-1}]} \ \)のときの誘導起電力\( \ \mathrm {[V]} \ \)
(3) 可逆チョッパに接続し,定格トルクを課した場合の最高回転速度\( \ \mathrm {[{min}^{-1}]} \ \)
(4) 回転速度\( \ 1 \ 000 \ \mathrm {[{min}^{-1}]} \ \)で,定格の\( \ 50 \ \mathrm {[%]} \ \)トルクの負荷を課した場合の電機子の端子電圧\( \ \mathrm {[V]} \ \)
(5) 上記(4)の運転状態とするための\( \ \mathrm {IGBT \ S_{1}} \ \)の通流率
(6) 制動トルクを定格トルクに制御できる回転速度\( \ \mathrm {[{min}^{-1}]} \ \)の範囲
【ワンポイント解説】
二次試験としては出題が珍しい直流電動機に関する問題です。
近年は直流機からの出題は稀であり,後半の問題の難易度が非常に高いので,完璧に理解する必要はないかもしれませんが,直流機と可逆チョッパを組み合わせたやや難しめの問題なので,演習としてはやりがいのある問題であると思います。
1.直流他励電動機の等価回路
図3に直流他励電動機の等価回路を示します。図3において,\( \ V \ \)は端子電圧,\( \ E \ \)は逆起電力,\( \ V_{\mathrm {f}} \ \)は界磁電圧,\( \ I_{\mathrm {a}} \ \)は電機子電流,\( \ I_{\mathrm {f}} \ \)は界磁電流,\( \ R_{\mathrm {a}} \ \)は電機子抵抗,\( \ R_{\mathrm {f}} \ \)は界磁抵抗となります。
他励式の特徴としては,界磁回路が独立しているので,界磁磁束を独立して制御できるという特徴があります。
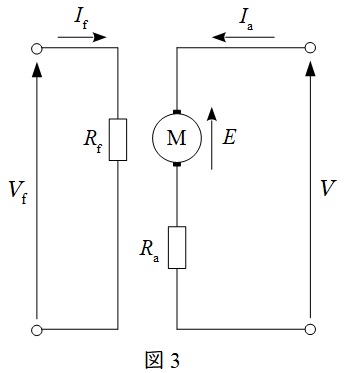
また,上記の等価回路にキルヒホッフの法則を適用すると,以下の関係式が導き出せることが分かります。
\[
\begin{eqnarray}
V &=& E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
I_{\mathrm {f}} &=& \frac {E_{\mathrm {f}}}{R_{\mathrm {f}}} \\[ 5pt ]
\end{eqnarray}
\]
2.直流機の誘導起電力(逆起電力)\( \ E \ \)
磁極の数\( \ p \ \),電機子導体数\( \ Z \ \),電機子巻線並列回路数\( \ a \ \),各極の磁束\( \ \phi \ \),回転速度\( \ N \ \)とすると,直流機の誘導起電力(逆起電力)\( \ E \ \)は,
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ]
&=&k_{\mathrm {e}}\phi N \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)と回転速度\( \ N \ \)に比例します。
3.直流機のトルク\( \ T \ \)
磁極の数\( \ p \ \),電機子導体数\( \ Z \ \),電機子巻線並列回路数\( \ a \ \),各極の磁束\( \ \phi \ \),電機子電流\( \ I_{\mathrm {a}} \ \)とすると,直流機のトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=&\frac {pZ}{2\pi a}\phi I_{\mathrm {a}} \\[ 5pt ]
&=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)と電機子電流\( \ I_{\mathrm {a}} \ \)に比例します。
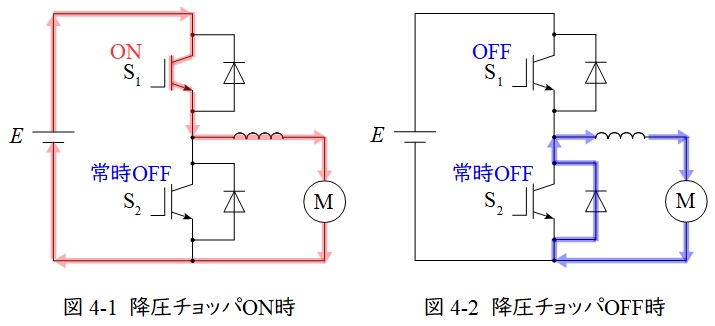
4.可逆チョッパ
降圧チョッパを昇圧チョッパを組み合わせたようなチョッパで,電源電圧と異なる負荷に電力を供給することと負荷の制動トルクを電源に回生することの両方が可能となります。
①降圧チョッパとして動作する時
図4-1及び図4-2のように動作します。
スイッチ\( \ \mathrm {S_{2}} \ \)は常時\( \ \mathrm {OFF} \ \)でスイッチ\( \ \mathrm {S_{1}} \ \)で\( \ \mathrm {ON-OFF} \ \)制御します。
\( \ \mathrm {S_{1}} \ \)が\( \ \mathrm {ON} \ \)の時,図4-1のように電源-\( \ \mathrm {S_{1}} \ \)-リアクトル-負荷-電源と導通し,リアクトルと負荷に電力が供給されます。
\( \ \mathrm {S_{1}} \ \)が\( \ \mathrm {OFF} \ \)の時,図4-2のようにリアクトル-負荷-ダイオード-リアクトルと導通し,リアクトルに蓄えられているエネルギーが放出されます。
全体としてリアクトルに蓄えられるエネルギーと放出されるエネルギーの量が等しいので,負荷電圧を\( \ V \ \)とすると,
\[
\begin{eqnarray}
\left( E-V\right)IT_{\mathrm {on}} &=&VIT_{\mathrm {off}} \\[ 5pt ]
\left( E-V\right)T_{\mathrm {on}} &=&VT_{\mathrm {off}} \\[ 5pt ]
ET_{\mathrm {on}} &=&V\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) \\[ 5pt ]
V &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ]
&=&\alpha E \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \alpha =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ \)を通流率といいます。\( \ \alpha <1 \ \)なので,\( \ E>V \ \)となります。
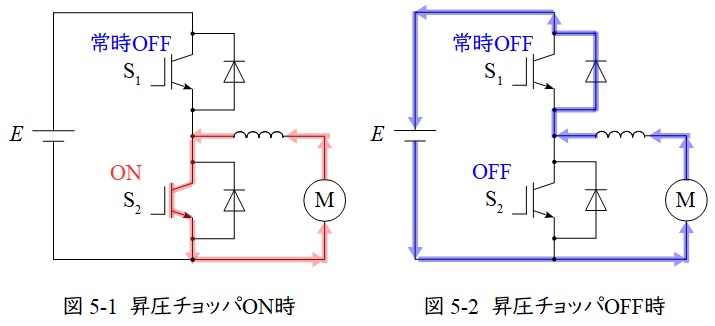
②昇圧チョッパとして動作する時
図5-1及び図5-2のように動作します。
スイッチ\( \ \mathrm {S_{1}} \ \)は常時\( \ \mathrm {OFF} \ \)でスイッチ\( \ \mathrm {S_{2}} \ \)で\( \ \mathrm {ON-OFF} \ \)制御します。
\( \ \mathrm {S_{2}} \ \)が\( \ \mathrm {ON} \ \)の時,図5-1のように負荷-リアクトル-\( \ \mathrm {S_{2}} \ \)-負荷と導通し,負荷からの回生エネルギーがリアクトルに蓄えられます。
\( \ \mathrm {S_{2}} \ \)が\( \ \mathrm {OFF} \ \)の時,図5-2のようにリアクトル-ダイオード-電源-負荷-リアクトルと導通し,リアクトルに蓄えられているエネルギーが放出され,電源に回生されます。
全体としてリアクトルに蓄えられるエネルギーと放出されるエネルギーの量が等しいので,負荷電圧を\( \ V \ \)とすると,
\[
\begin{eqnarray}
VIT_{\mathrm {on}} &=&\left( E-V\right) IT_{\mathrm {off}} \\[ 5pt ]
VT_{\mathrm {on}} &=&\left( E-V\right) T_{\mathrm {off}} \\[ 5pt ]
V\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) &=&ET_{\mathrm {off}} \\[ 5pt ]
E &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V \\[ 5pt ]
\end{eqnarray}
\]
となります。上式を通流率\( \ \alpha \ \)を用いて表すと,
\[
\begin{eqnarray}
\alpha &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \\[ 5pt ]
\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) \alpha &=&T_{\mathrm {on}} \\[ 5pt ]
\alpha T_{\mathrm {off}}&=&\left( 1-\alpha \right) T_{\mathrm {on}} \\[ 5pt ]
T_{\mathrm {on}}&=&\frac {\alpha }{1-\alpha }T_{\mathrm {off}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
E &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V \\[ 5pt ]
&=&\left( 1+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}\right) V \\[ 5pt ]
&=&\left( 1+\frac {\displaystyle \frac {\alpha }{1-\alpha }T_{\mathrm {off}}}{T_{\mathrm {off}}}\right) V \\[ 5pt ]
&=&\left( 1+\frac {\alpha }{1-\alpha }\right) V \\[ 5pt ]
&=&\frac {1}{1-\alpha } V \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ V<E \ \)となります。
【解答】
(1)電機子巻線抵抗\( \ \mathrm {[\Omega ]} \ \)
図3の等価回路において,題意より,直流電圧\( \ V=200 \ \mathrm {[V]} \ \),軸出力\( \ P=3.75 \ \mathrm {[kW]} \ \),回転速度\( \ N=1 \ 500 \ \mathrm {[{min}^{-1}]} \ \),電機子電流\( \ I_{\mathrm {a}}=20 \ \mathrm {[A]} \ \),ブラシの電圧降下\( \ v=2.5 \ \mathrm {[V]} \ \)である。
逆起電力(誘導起電力)を\( \ E \ \mathrm {[V]} \ \)とすると,
\[
\begin{eqnarray}
E &=&\frac {P}{I_{\mathrm {a}}} \\[ 5pt ]
&=&\frac {3.75\times 10^{3}}{20} \\[ 5pt ]
&=&187.5 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,回路方程式をたてると,
\[
\begin{eqnarray}
V &=& E+R_{\mathrm {a}}I_{\mathrm {a}}+v \\[ 5pt ]
R_{\mathrm {a}}I_{\mathrm {a}}&=&V-E-v \\[ 5pt ]
R_{\mathrm {a}}&=&\frac {V-E-v}{I_{\mathrm {a}}} \\[ 5pt ]
&=&\frac {200-187.5-2.5}{20} \\[ 5pt ]
&=&0.5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)定格トルクと課し,回転速度が\( \ 1 \ 500 \ \mathrm {[{min}^{-1}]} \ \)のときの誘導起電力\( \ \mathrm {[V]} \ \)
ワンポイント解説「3.直流機のトルク\( \ T \ \)」の通り,トルクと電機子電流は比例し,ワンポイント解説「2.直流機の誘導起電力(逆起電力)\( \ E \ \)」の通り,誘導起電力と回転数は比例するので,定格トルクと課し,回転速度が\( \ 1 \ 500 \ \mathrm {[{min}^{-1}]} \ \)の誘導起電力は(1)で導出した誘導起電力となる。したがって,
\[
\begin{eqnarray}
E &=&187.5 → 188 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)可逆チョッパに接続し,定格トルクを課した場合の最高回転速度\( \ \mathrm {[{min}^{-1}]} \ \)
ワンポイント解説「3.直流機のトルク\( \ T \ \)」トルクと電機子電流\( \ I_{\mathrm {a}} \ \)は比例するので,定格トルクを課した場合の電機子電流は,\( \ I_{\mathrm {a}}=20 \ \mathrm {[A]} \ \)である。
図4-1において,\( \ \mathrm {IGBT} \ \)の電圧降下は\( \ v_{\mathrm {I}}=2 \ \mathrm {[V]} \ \)であるから,このときの逆起電力(誘導起電力)\( \ E^{\prime } \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V-v_{\mathrm {I}} &=& E^{\prime }+R_{\mathrm {a}}I_{\mathrm {a}}+v \\[ 5pt ]
E^{\prime }&=&V-v_{\mathrm {I}}-R_{\mathrm {a}}I_{\mathrm {a}}-v \\[ 5pt ]
&=&200-2-0.5\times 20 -2.5 \\[ 5pt ]
&=&185.5 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,そのときの回転速度\( \ N^{\prime } \ \mathrm {[{min}^{-1}]} \ \)は,ワンポイント解説「2.直流機の誘導起電力(逆起電力)\( \ E \ \)」より誘導起電力と回転数が比例するので,
\[
\begin{eqnarray}
\frac {N^{\prime }}{N} &=& \frac {E^{\prime }}{E} \\[ 5pt ]
N^{\prime }&=&\frac {E^{\prime }}{E}N \\[ 5pt ]
&=&\frac {185.5}{187.5}\times 1500 \\[ 5pt ]
&=&1484 → 1480 \mathrm {[{min}^{-1}]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)回転速度\( \ 1 \ 000 \ \mathrm {[{min}^{-1}]} \ \)で,定格の\( \ 50 \ \mathrm {[%]} \ \)トルクの負荷を課した場合の電機子の端子電圧\( \ \mathrm {[V]} \ \)
回転速度\( \ N^{\prime \prime }=1 \ 000 \ \mathrm {[{min}^{-1}]} \ \)の時の誘導起電力\( \ E^{\prime \prime } \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\frac {N^{\prime \prime }}{N} &=& \frac {E^{\prime \prime }}{E} \\[ 5pt ]
E^{\prime \prime }&=&\frac {N^{\prime \prime }}{N}E \\[ 5pt ]
&=&\frac {1000}{1500}\times 187.5 \\[ 5pt ]
&=&125 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ 50 \ \mathrm {[%]} \ \)トルクの時の電機子電流\( \ I_{\mathrm {a}}^{\prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {a}}^{\prime } &=& 0.5I_{\mathrm {a}} \\[ 5pt ]
&=&0.5\times 20 \\[ 5pt ]
&=&10 \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,そのときの電機子の端子電圧\( \ V^{\prime } \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V^{\prime } &=& E^{\prime \prime }+R_{\mathrm {a}}I_{\mathrm {a}}^{\prime }+v \\[ 5pt ]
&=&125+0.5\times 10+2.5 \\[ 5pt ]
&=&132.5 → 133 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)(4)の運転状態とするための\( \ \mathrm {IGBT \ S_{1}} \ \)の通流率
\( \ \mathrm {IGBT \ S_{1}} \ \)が\( \ \mathrm {ON} \ \)の時の端子電圧\( \ V_{\mathrm {on}} \ \mathrm {[V]} \ \)は,\( \ \mathrm {IGBT} \ \)の電圧降下は\( \ v_{\mathrm {I}}=2 \ \mathrm {[V]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {on}} &=& V-v_{\mathrm {I}} \\[ 5pt ]
&=&200-2 \\[ 5pt ]
&=&198 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \mathrm {IGBT \ S_{1}} \ \)が\( \ \mathrm {OFF} \ \)の時の端子電圧\( \ V_{\mathrm {off}} \ \mathrm {[V]} \ \)は,逆並列ダイオードの電圧降下は\( \ v_{\mathrm {D}}=1 \ \mathrm {[V]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {off}} &=& -v_{\mathrm {D}} \\[ 5pt ]
&=&-1 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,電機子の端子電圧\( \ V^{\prime } \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V^{\prime } &=& \frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {on}}+\frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {off}} \\[ 5pt ]
&=& \alpha V_{\mathrm {on}}+\left( 1-\alpha \right) V_{\mathrm {off}} \\[ 5pt ]
&=& \alpha \left( V_{\mathrm {on}}-V_{\mathrm {off}}\right) + V_{\mathrm {off}} \\[ 5pt ]
\end{eqnarray}
\]
という関係式が導かれ,
\[
\begin{eqnarray}
\alpha &=&\frac {V^{\prime }-V_{\mathrm {off}}}{V_{\mathrm {on}}-V_{\mathrm {off}}} \\[ 5pt ]
&=&\frac {132.5+1}{198+1} \\[ 5pt ]
&≒&0.67085 → 0.671 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)制動トルクを定格トルクに制御できる回転速度\( \ \mathrm {[{min}^{-1}]} \ \)の範囲
制動トルクを得るときは可逆チョッパは昇圧チョッパとして働くので,図5-1及び図5-2のように動作する。
端子電圧の取り得る範囲は\( \ \mathrm {IGBT \ S_{2}} \ \)が常時\( \ \mathrm {ON} \ \)と常時\( \ \mathrm {OFF} \ \)の範囲となる。\( \ \mathrm {IGBT \ S_{2}} \ \)が\( \ \mathrm {ON} \ \)の時の端子電圧\( \ V_{\mathrm {on}}^{* } \ \mathrm {[V]} \ \)は,\( \ \mathrm {IGBT} \ \)の電圧降下は\( \ v_{\mathrm {I}}=2 \ \mathrm {[V]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {on}}^{* } &=& v_{\mathrm {I}} \\[ 5pt ]
&=&2 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \mathrm {IGBT \ S_{2}} \ \)が\( \ \mathrm {OFF} \ \)の時の端子電圧\( \ V_{\mathrm {off}}^{* } \ \mathrm {[V]} \ \)は,逆並列ダイオードの電圧降下が\( \ v_{\mathrm {D}}=1 \ \mathrm {[V]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {off}}^{* } &=& E+v_{\mathrm {D}} \\[ 5pt ]
&=& 200+1 \\[ 5pt ]
&=&201 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また他励直流電動機が発電機として働くときの誘導起電力\( \ E^{* } \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
E^{* } &=& V^{* }+R_{\mathrm {a}}I_{\mathrm {a}}+v \\[ 5pt ]
\end{eqnarray}
\]
となり,制動トルクを定格トルクに制御できるとは,電機子電流\( \ I_{\mathrm {a}}=20 \ \mathrm {[A]} \ \)であることなので,
\[
\begin{eqnarray}
E^{* } &=& V^{* }+0.5\times 20+2.5 \\[ 5pt ]
&=& V^{* }+12.5 \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導起電力の取り得る範囲は,
\[
\begin{eqnarray}
E_{\mathrm {on}}^{* } &=& V_{\mathrm {on}}^{* }+12.5 \\[ 5pt ]
&=& 2+12.5 \\[ 5pt ]
&=&14.5 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
E_{\mathrm {off}}^{* } &=& V_{\mathrm {off}}^{* }+12.5 \\[ 5pt ]
&=& 201+12.5 \\[ 5pt ]
&=&213.5 \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その時の各回転数\( \ N_{\mathrm {on}}^{* } \ \mathrm {[{min}^{-1}]} \ \)及び\( \ N_{\mathrm {off}}^{* } \ \mathrm {[{min}^{-1}]} \ \)は,
\[
\begin{eqnarray}
\frac {N_{\mathrm {on}}^{* }}{N} &=& \frac {E_{\mathrm {on}}^{* }}{E} \\[ 5pt ]
N_{\mathrm {on}}^{* }&=&\frac {E_{\mathrm {on}}^{* }}{E}N \\[ 5pt ]
&=&\frac {14.5}{187.5}\times 1500 \\[ 5pt ]
&=&116 \mathrm {[{min}^{-1}]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\frac {N_{\mathrm {off}}^{* }}{N} &=& \frac {E_{\mathrm {off}}^{* }}{E} \\[ 5pt ]
N_{\mathrm {off}}^{* }&=&\frac {E_{\mathrm {off}}^{* }}{E}N \\[ 5pt ]
&=&\frac {213.5}{187.5}\times 1500 \\[ 5pt ]
&=&1708 → 1710 \mathrm {[{min}^{-1}]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,制御できる回転速度は\( \ 116~1710 \ \mathrm {[{min}^{-1}]} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは