Contents
【問題】
【難易度】★★★★☆(やや難しい)
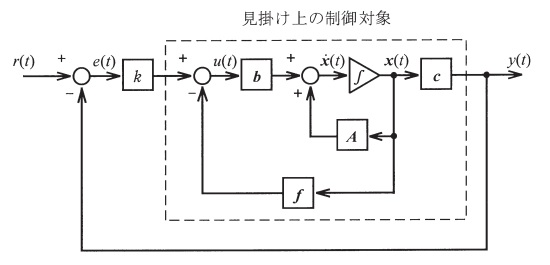
図に示す構造の制御系を考える。ここで\( \ r\left( t\right) \ \)は目標値,\( \ e\left( t\right) \ \)は制御偏差,\( \ u\left( t\right) \ \)は入力,\( \ \boldsymbol x\left( t\right) \ \)は状態,\( \ y\left( t\right) \ \)は出力を表し,制御対象は次の状態方程式で記述される。
\[
\boldsymbol {\dot x}\left( t \right) =\boldsymbol A\boldsymbol x\left( t\right)+\boldsymbol b u\left( t\right)
\]
\[
y \left( t \right) = \boldsymbol c\boldsymbol x\left( t\right)
\]
\[
\boldsymbol A =\begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix},\boldsymbol b =\begin{pmatrix} 0 \\ 1 \end{pmatrix},\boldsymbol c =\begin{pmatrix} 2 & 1 \end{pmatrix}
\]
次の問に答えよ。
(1) 図中の直列補償器のゲイン\( \ k \ \)を零として,状態フィードバック係数ベクトル\( \ \boldsymbol f =\begin{pmatrix} f_{1} & f_{2} \end{pmatrix} \ \)を用いて見掛け上の制御対象の特性改善を図る。行列\( \ \boldsymbol A -\boldsymbol b \boldsymbol f \ \)の固有値を\( \ -3 \ \),\( \ -4 \ \)に配置する\( \ \boldsymbol f \ \)を計算せよ。
(2) 上記小問(1)で求めた\( \ \boldsymbol f \ \)を用いて特性改善をした見掛け上の制御対象に対して,目標値\( \ r\left( t\right) \ \)に出力\( \ y\left( t\right) \ \)が追従することを目的に,図に示すフィードバック制御系を構成した。閉ループ系が安定になるように直列補償器のゲイン\( \ k \ \)を設計できたとするとき,入力\( \ u\left( t\right) \ \)を\( \ \boldsymbol x\left( t\right) \ \),\( \ r\left( t\right) \ \),\( \ \boldsymbol c \ \),\( \ \boldsymbol f \ \),\( \ k \ \)を用いて表せ。
(3) 上記小問(2)の入力\( \ u\left( t\right) \ \)を制御対象に加える。閉ループ系の状態方程式を\( \ \boldsymbol {\dot x}\left( t \right) \ \),\( \ \boldsymbol x\left( t\right) \ \),\( \ r\left( t\right) \ \),\( \ \boldsymbol A \ \),\( \ \boldsymbol b \ \),\( \ \boldsymbol c \ \),\( \ \boldsymbol f \ \),\( \ k \ \)を用いて表せ。
(4) 上記小問(3)で求めた状態方程式の中の\( \ \boldsymbol A \ \),\( \ \boldsymbol b \ \),\( \ \boldsymbol c \ \),\( \ \boldsymbol f \ \)に,与えられた数値及び上記小問(1)で求めた数値を代入して整理せよ。ただし,\( \ k \ \)は変数のままとする。
(5) 目標値の大きさ\( \ r_{0} \ \)でステップ状に変化させる場合を考える。上記小問(2)の仮定より閉ループ系は安定なので,状態\( \ \boldsymbol x\left( t\right) \ \)は定常,すなわち\( \ \boldsymbol {\dot x}\left( \infty \right) =\begin{pmatrix} 0 \\ 0 \end{pmatrix} \ \)となる。このときの定常値\( \ \boldsymbol x\left( \infty \right) \ \)を\( \ k \ \)と\( \ r_{0} \ \)を用いて表せ。
(6) 関係式\( \ e\left( \infty \right) =r_{0} -y\left( \infty \right) =r_{0}-\boldsymbol c\boldsymbol x\left( \infty \right) \ \)を使って,定常偏差\( \ e\left( \infty \right) \ \)を\( \ k \ \)と\( \ r_{0} \ \)を用いて表せ。
【ワンポイント解説】
現代制御理論は一種では何度も出題されていましたが,二種では初めての出題となりました。しかしながら,一度出題されたということは今後も出題される可能性があります。一種の過去問等も参考に対策を講じましょう。
1.行列の固有値
行列\( \ \boldsymbol A =\begin{pmatrix} a & b \\ c & d \end{pmatrix} \ \)の固有値は,単位行列\( \ \boldsymbol I =\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \ \)とすると,\( \ \det \left[ s\boldsymbol I-\boldsymbol A \right]=0 \ \)の解です。具体的には,
\[
\begin{eqnarray}
\det \left[ s\boldsymbol I-\boldsymbol A \right] &=& 0 \\[ 5pt ]
\det \left[ s\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}-\begin{pmatrix} a & b \\ c & d \end{pmatrix} \right] &=& 0 \\[ 5pt ]
\det \begin{bmatrix} s-a & -b \\ -c & s-d \end{bmatrix} &=& 0\\[ 5pt ]
\left( s-a \right) \left( s-d \right) -bc &=& 0 \\[ 5pt ]
s^{2}-\left( a+d \right) s+ad-bc &=& 0
\end{eqnarray}
\]
の\( \ s \ \)の解となります。
【解答】
(1)行列\( \ \boldsymbol A -\boldsymbol b \boldsymbol f \ \)の固有値を\( \ -3 \ \),\( \ -4 \ \)に配置する\( \ \boldsymbol f \ \)
\( \ \boldsymbol A -\boldsymbol b \boldsymbol f \ \)に各値を代入して整理すると,
\[
\begin{eqnarray}
\boldsymbol A -\boldsymbol b \boldsymbol f &=& \begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix} -\begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} f_{1} & f_{2} \end{pmatrix} \\[ 5pt ]
&=& \begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix} -\begin{pmatrix} 0 & 0 \\ f_{1} & f_{2} \end{pmatrix} \\[ 5pt ]
&=& \begin{pmatrix} 0 & 1 \\ -f_{1} & -1-f_{2} \end{pmatrix}
\end{eqnarray}
\]
となるから,ワンポイント解説「1.行列の固有値」より行列\( \ \boldsymbol A -\boldsymbol b \boldsymbol f \ \)の固有値は,
\[
\begin{eqnarray}
\det \left[ s\boldsymbol I-\left( \boldsymbol A -\boldsymbol b \boldsymbol f\right) \right] &=& 0 \\[ 5pt ]
\det \left[ s\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}-\begin{pmatrix} 0 & 1 \\ -f_{1} & -1-f_{2} \end{pmatrix} \right] &=& 0 \\[ 5pt ]
\det \begin{bmatrix} s & -1 \\ f_{1} & s+1+f_{2} \end{bmatrix} &=& 0\\[ 5pt ]
s \left( s+1+f_{2} \right) +f_{1} &=& 0 \\[ 5pt ]
s^{2}+\left( 1+f_{2} \right) s+f_{1} &=& 0
\end{eqnarray}
\]
の解となる。この解が\( \ -3 \ \),\( \ -4 \ \)となるためには,
\[
\begin{eqnarray}
\left( s+3\right) \left( s+4\right) &=& 0 \\[ 5pt ]
s^{2}+7 s+12 &=& 0
\end{eqnarray}
\]
と各係数が一致しなければならない。よって,係数比較をすると,
\[
\begin{eqnarray}
1+f_{2}&=&7 ⇔ f_{2}=6 \\[ 5pt ]
f_{1} &=& 12
\end{eqnarray}
\]
となるため,求める行列\( \ \boldsymbol f \ \)は\( \ \boldsymbol f=\begin{pmatrix} 12 & 6 \end{pmatrix} \ \)となる。
(2)入力\( \ u\left( t\right) \ \)を\( \ \boldsymbol x\left( t\right) \ \),\( \ r\left( t\right) \ \),\( \ \boldsymbol c \ \),\( \ \boldsymbol f \ \),\( \ k \ \)を用いて表す
問題図より,以下の2式が導ける。
\[
\begin{eqnarray}
u\left( t\right) &=& -\boldsymbol f\boldsymbol x\left( t\right)+ke\left( t\right) &・・・・・・・・・・①&\\[ 5pt ]
e\left( t\right) &=& r\left( t\right) -\boldsymbol c \boldsymbol x\left( t\right) &・・・・・・・・・・②&
\end{eqnarray}
\]
②を①に代入すると,
\[
\begin{eqnarray}
u\left( t\right) &=& -\boldsymbol f\boldsymbol x\left( t\right)+ke\left( t\right) \\[ 5pt ]
&=& -\boldsymbol f\boldsymbol x\left( t\right)+k\left\{ r\left( t\right) -\boldsymbol c \boldsymbol x\left( t\right) \right\} \\[ 5pt ]
&=& -\left( \boldsymbol f+k\boldsymbol c\right) \boldsymbol x\left( t\right) +kr\left( t\right)
\end{eqnarray}
\]
と求められる。
(3)状態方程式を\( \ \boldsymbol {\dot x}\left( t \right) \ \),\( \ \boldsymbol x\left( t\right) \ \),\( \ r\left( t\right) \ \),\( \ \boldsymbol A \ \),\( \ \boldsymbol b \ \),\( \ \boldsymbol c \ \),\( \ \boldsymbol f \ \),\( \ k \ \)を用いて表す
(2)の解答式を状態方程式に代入すると,
\[
\begin{eqnarray}
\boldsymbol {\dot x}\left( t \right) &=& \boldsymbol A\boldsymbol x\left( t\right)+\boldsymbol b u\left( t\right) \\[ 5pt ]
&=& \boldsymbol A\boldsymbol x\left( t\right)+\boldsymbol b \left\{ -\left( \boldsymbol f+k\boldsymbol c\right) \boldsymbol x\left( t\right) +kr\left( t\right)\right\} \\[ 5pt ]
&=& \left( \boldsymbol A – \boldsymbol b \boldsymbol f – \boldsymbol b k\boldsymbol c \right) \boldsymbol x\left( t\right) +\boldsymbol b kr\left( t\right)
\end{eqnarray}
\]
と求められる。
(4)与えられた数値及び上記小問(1)で求めた数値を代入して整理
(2)の解答式に題意に沿って各値を代入すると,
\[
\begin{eqnarray}
\boldsymbol {\dot x}\left( t \right) &=& \left( \boldsymbol A – \boldsymbol b \boldsymbol f – \boldsymbol b k\boldsymbol c \right) \boldsymbol x\left( t\right) +\boldsymbol b kr\left( t\right) \\[ 5pt ]
&=& \left[ \begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix} – \begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} 12 & 6 \end{pmatrix} – \begin{pmatrix} 0 \\ 1 \end{pmatrix} k\begin{pmatrix} 2 & 1 \end{pmatrix} \right] \boldsymbol x\left( t\right) +\begin{pmatrix} 0 \\ 1 \end{pmatrix} kr\left( t\right) \\[ 5pt ]
&=& \left[ \begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix} – \begin{pmatrix} 0 & 0 \\ 12 & 6 \end{pmatrix} – \begin{pmatrix} 0 & 0 \\ 2k & k \end{pmatrix} \right] \boldsymbol x\left( t\right) +\begin{pmatrix} 0 \\ k \end{pmatrix} r\left( t\right) \\[ 5pt ]
&=& \begin{pmatrix} 0 & 1 \\ -12-2k & -7-k \end{pmatrix} \boldsymbol x\left( t\right) +\begin{pmatrix} 0 \\ k \end{pmatrix} r\left( t\right)
\end{eqnarray}
\]
と求められる。
(5)定常値\( \ \boldsymbol x\left( \infty \right) \ \)を\( \ k \ \)と\( \ r_{0} \ \)を用いて表す
\( \ r_{0} \ \)は目標値であるため,閉ループ系が安定であれば,\( \ r\left( \infty \right) =r_{0} \ \)となる。\( \ \boldsymbol x\left( \infty \right)= \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} \ \)とおくと,(4)の解答式は,
\[
\begin{eqnarray}
\boldsymbol {\dot x}\left( \infty \right) &=& \begin{pmatrix} 0 & 1 \\ -12-2k & -7-k \end{pmatrix} \boldsymbol x\left( \infty \right) +\begin{pmatrix} 0 \\ k \end{pmatrix} r\left( \infty \right) \\[ 5pt ]
\begin{pmatrix} 0 \\ 0 \end{pmatrix} &=& \begin{pmatrix} 0 & 1 \\ -12-2k & -7-k \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} +\begin{pmatrix} 0 \\ k \end{pmatrix} r_{0}\\[ 5pt ]
\begin{pmatrix} 0 \\ 0 \end{pmatrix} &=& \begin{pmatrix} x_{2} \\ -2\left( 6 +k\right) x_{1} -\left( 7 +k\right) x_{2} +k r_{0} \end{pmatrix}
\end{eqnarray}
\]
となる。両辺の係数比較をすることにより,
\[
\begin{eqnarray}
x_{2} &=& 0 \\[ 5pt ]
0 &=& -2\left( 6 +k\right) x_{1}+k r_{0} ⇔ x_{1}=\frac {k r_{0}}{2\left( 6 +k\right) }
\end{eqnarray}
\]
と求められるので,\( \ \boldsymbol x\left( \infty \right) = \begin{pmatrix} \frac {k r_{0}}{2\left( 6 +k\right)} \\ 0 \end{pmatrix} \ \)となる。
(6)定常偏差\( \ e\left( \infty \right) \ \)を\( \ k \ \)と\( \ r_{0} \ \)を用いて表す
題意より,\( \ e\left( \infty \right) =r_{0} -y\left( \infty \right) =r_{0}-\boldsymbol c\boldsymbol x\left( \infty \right) \ \)であるから,
\[
\begin{eqnarray}
e\left( \infty \right) &=& r_{0}-\boldsymbol c\boldsymbol x\left( \infty \right) \\[ 5pt ]
&=& r_{0}-\begin{pmatrix} 2 & 1 \end{pmatrix}\begin{pmatrix} \frac {k r_{0}}{2\left( 6 +k\right)} \\ 0 \end{pmatrix} \\[ 5pt ]
&=& r_{0}-\frac {k r_{0}}{6 +k} \\[ 5pt ]
&=& \frac {6 r_{0}}{6 +k}
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは