【問題】
【難易度】★★★☆☆(普通)
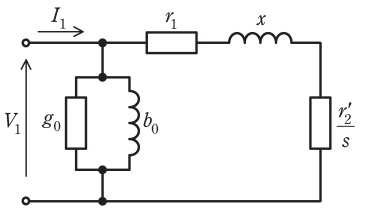
滑り\( \ s \ \)で運転している三相誘導電動機の星形結線一相当たりの\( \ \mathrm {L} \ \)形等価回路を下図に示す。回路定数はそれぞれ以下のとおりである。ただし,等価回路の端子電圧(相電圧)を\( \ V_{\mathrm {1}} \ \),入力電流を\( \ I_{\mathrm {1}} \ \),電源周波数を\( \ f \ \),極対数を\( \ p \ \)とし,等価回路の励磁コンダクタンス\( \ g_{\mathrm {0}} \ \)及び励磁サセプタンス\( \ b_{\mathrm {0}} \ \)は無視できるものとする。
\[
\begin{eqnarray}
g_{\mathrm {0}} &:&励磁コンダクタンス \\[ 5pt ]
b_{\mathrm {0}} &:&励磁サセプタンス \\[ 5pt ]
r_{\mathrm {1}} &:&一次抵抗 \\[ 5pt ]
r_{\mathrm {2}}^{\prime } &:&一次換算二次抵抗 \\[ 5pt ]
x &:&漏れリアクタンス \\[ 5pt ]
\end{eqnarray}
\]
次の問については,図に記載されている記号を用いて答えよ。
(1) 入力電流\( \ I_{\mathrm {1}} \ \)の式を求めよ。
(2) 機械的出力\( \ P_{\mathrm {o}} \ \)の式を求めよ。
(3) 同期角速度\( \ \omega _{\mathrm {s}} \ \)を電源周波数\( \ f \ \)及び極対数\( \ p \ \)を用いて表せ。
(4) この誘導電動機の発生トルク\( \ T \ \)の式を求めよ。
(5) 最大トルクが得られる滑り\( \ s_{\mathrm {m}} \ \)の式を求めよ。
(6) 最大トルク\( \ T_{\mathrm {m}} \ \)の式を求めよ。
【ワンポイント解説】
誘導電動機の諸計算に関する問題です。
難易度はそれほど高い内容ではありませんが,極数が極対数(\( \ \mathrm {N} \ \)及び\( \ \mathrm {S} \ \)の\( \ 2 \ \)極で\( \ 1 \ \)極対)となっているのと,設問数が多く計算量が多いので時間がかかるのが気になる問題です。演習を繰り返しできるだけ迷わずに\( \ 30 \ \)分以内に解けるようになると良いと思います。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,同期角速度\( \ \omega _{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ]
&=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ]
&=&\frac {4\pi f}{p} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \),回転数が\( \ N \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \)は一次電流,\( \ {\dot I}_{2} \ \)は二次電流,\( \ {\dot I}_{0} \ \)は励磁電流,\( \ r_{1} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
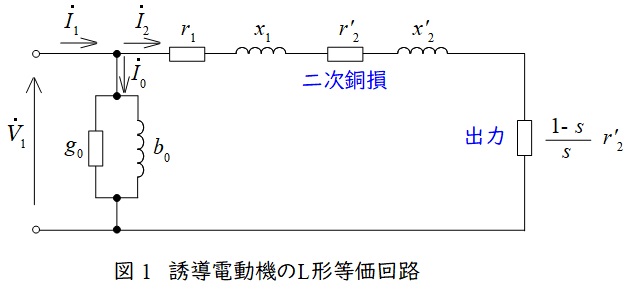
図1より,
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,二次入力\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ]
&=&3\frac {r_{2}^{\prime}}{s}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right) ^{2} \\[ 5pt ]
&=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\]
となり,発生するトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {(1-s)P_{2}}{(1-s)\omega _{s}} \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ]
&=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)入力電流\( \ I_{\mathrm {1}} \ \)
励磁コンダクタンス\( \ g_{\mathrm {0}} \ \)及び励磁サセプタンス\( \ b_{\mathrm {0}} \ \)は無視できるので,回路方程式から,
\[
\begin{eqnarray}
I_{\mathrm {1}} &=& \frac {V_{\mathrm {1}}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +x ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)機械的出力\( \ P_{\mathrm {o}} \ \)
ワンポイント解説「3.誘導電動機の\( \ \mathrm {L} \ \)形等価回路」の通り,
\[
\begin{eqnarray}
\frac {r_{2}^{\prime}}{s} &=&r_{2}^{\prime}+\frac {1-s}{s}r_{2}^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
と分けることができ,出力は\( \ \displaystyle \frac {1-s}{s}r_{2}^{\prime } \ \)で消費される電力なので,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=&3\frac {1-s}{s}r_{2}^{\prime }I_{\mathrm {1}}^{2} \\[ 5pt ]
&=&3\frac {1-s}{s}r_{2}^{\prime }\left\{ \frac {V_{\mathrm {1}}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +x ^{2}}}\right\} ^{2} \\[ 5pt ]
&=&3\frac {1-s}{s}r_{2}^{\prime } \cdot \frac {V_{\mathrm {1}}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +x ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)同期角速度\( \ \omega _{\mathrm {s}} \ \)
ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)」に与えられている式において,極数を与えられている極対数から\( \ \displaystyle 2p \ \)とすれば良いので,同期角速度\( \ \omega _{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {4\pi f}{2p} \\[ 5pt ]
&=&\frac {2\pi f}{p} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)発生トルク\( \ T \ \)
ワンポイント解説「3.誘導電動機の\( \ \mathrm {L} \ \)形等価回路」の通り,二次入力\( \ P_{\mathrm {2}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {2}}&=&3\frac {r_{2}^{\prime}}{s}{I_{\mathrm {1}}}^{2} \\[ 5pt ]
&=&3\frac {r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +x ^{2}}
\end{eqnarray}
\]
となるので,発生トルク\( \ T \ \)は,
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {(1-s)P_{2}}{(1-s)\omega _{s}} \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ]
&=&3\frac {r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +x ^{2}}\cdot \frac {p}{2\pi f} \\[ 5pt ]
&=&\frac {3pr_{2}^{\prime}}{2\pi fs}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +x ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)最大トルクが得られる滑り\( \ s_{\mathrm {m}} \ \)
(4)の解答式を整理すると,
\[
\begin{eqnarray}
T&=&\frac {3pr_{2}^{\prime}}{2\pi f}\cdot \frac {V_{1}^{2}}{\displaystyle s\left\{ \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +x ^{2}\right\} } \\[ 5pt ]
&=&\frac {3pr_{2}^{\prime}}{2\pi f}\cdot \frac {V_{1}^{2}}{\displaystyle s\left( r_{1}^{2}+\frac {2r_{1}r_{2}^{\prime}}{s}+ \frac {{r_{2}^{\prime }}^{2}}{s^{2}} +x ^{2}\right) } \\[ 5pt ]
&=&\frac {3pr_{2}^{\prime}}{2\pi f}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}^{2}+x ^{2}\right)s+2r_{1}r_{2}^{\prime}+ \frac {{r_{2}^{\prime }}^{2}}{s} } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle A=\left( r_{1}^{2}+x ^{2}\right)s+2r_{1}r_{2}^{\prime}+ \frac {{r_{2}^{\prime }}^{2}}{s} \ \)とすれば,\( \ A \ \)が最小となるとき最大トルクが得られる。\( \ A \ \)を\( \ s \ \)で微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}s}&=&r_{1}^{2}+x ^{2}- \frac {{r_{2}^{\prime }}^{2}}{s^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}s}=0 \ \)のとき最大トルクが得られる滑り\( \ s_{\mathrm {m}} \ \)となるので,
\[
\begin{eqnarray}
r_{1}^{2}+x ^{2}- \frac {{r_{2}^{\prime }}^{2}}{s_{\mathrm {m}}^{2}}&=&0 \\[ 5pt ]
\frac {{r_{2}^{\prime }}^{2}}{s_{\mathrm {m}}^{2}}&=&r_{1}^{2}+x ^{2} \\[ 5pt ]
s_{\mathrm {m}}^{2}&=&\frac {{r_{2}^{\prime }}^{2}}{r_{1}^{2}+x ^{2}} \\[ 5pt ]
s_{\mathrm {m}}&=& \frac {r_{2}^{\prime }}{\sqrt {r_{1}^{2}+x ^{2}}} \left( ∵s_{\mathrm {m}}>0\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)最大トルク\( \ T_{\mathrm {m}} \ \)
(5)の解答式を(4)解答式に代入すると最大トルク\( \ T_{\mathrm {m}} \ \)が求められるので,
\[
\begin{eqnarray}
T_{\mathrm {m}}&=&\frac {3pr_{2}^{\prime}}{2\pi fs_{\mathrm {m}}}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s_{\mathrm {m}}}\right) ^{2} +x ^{2}} \\[ 5pt ]
&=&\frac {3pr_{2}^{\prime}}{2\pi f}\cdot \frac {\sqrt {r_{1}^{2}+x ^{2}}}{r_{2}^{\prime }} \cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+r_{2}^{\prime}\cdot \frac {\sqrt {r_{1}^{2}+x ^{2}}}{r_{2}^{\prime }}\right) ^{2} +x ^{2}} \\[ 5pt ]
&=&\frac {3p}{2\pi f}\cdot \sqrt {r_{1}^{2}+x ^{2}} \cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\sqrt {r_{1}^{2}+x ^{2}}\right) ^{2} +x ^{2}} \\[ 5pt ]
&=&\frac {3p}{2\pi f}\cdot \sqrt {r_{1}^{2}+x ^{2}} \cdot \frac {V_{1}^{2}}{\displaystyle r_{1}^{2}+2r_{1}\sqrt {r_{1}^{2}+x ^{2}}+r_{1}^{2}+x ^{2} +x ^{2}} \\[ 5pt ]
&=&\frac {3p}{2\pi f}\cdot \sqrt {r_{1}^{2}+x ^{2}} \cdot \frac {V_{1}^{2}}{\displaystyle 2\left( r_{1}^{2}+x ^{2}+r_{1}\sqrt {r_{1}^{2}+x ^{2}}\right) } \\[ 5pt ]
&=&\frac {3p}{4\pi f} \cdot \frac {V_{1}^{2}}{\displaystyle \sqrt {r_{1}^{2}+x ^{2}}+r_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは