【問題】
【難易度】★★★☆☆(普通)
図に示すフィードバック制御系について,次の問に答えよ。ここで,\( \ R\left( s\right) \ \)は目標値,\( \ E\left( s\right) \ \)は制御偏差,\( \ Y\left( s\right) \ \)は制御量であり,\( \ K>0 \ \)とする。
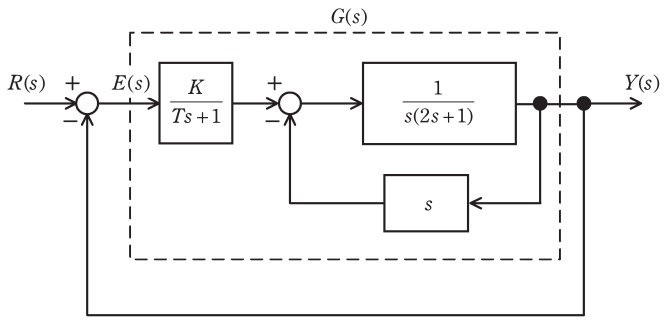
(1) 開ループ伝達関数\( \ \displaystyle G\left( s\right) =\frac {Y\left( s\right) }{E\left( s\right) } \ \)を求めよ。
(2) 閉ループ伝達関数\( \ \displaystyle W\left( s\right) =\frac {Y\left( s\right) }{R\left( s\right) } \ \)を求めよ。
(3) この制御系において,\( \ T=0 \ \)としたとき,閉ループ伝達関数\( \ W\left( s\right) \ \)の特性方程式は二次方程式となる。目標値のステップ状変化に対する制御量の時間応答\( \ y\left( t\right) \ \)が振動的になる\( \ K \ \)の条件を求めよ。
(4) 小問(3)の制御系において\( \ K=1 \ \)としたとき,目標値の単位インパルス変化に対する制御量の時間応答\( \ y\left( t\right) \ \)を求めよ。
必要に応じて,ラプラス変換の複素領域における推移定理である\( \ \mathcal {L} \left[ \mathrm {e}^{-at}x\left( t \right) \right] =X\left( s+a\right) \ \)を使ってよい。
(5) この制御系において,\( \ T=2 \ \)としたとき,閉ループ伝達関数\( \ W\left( s\right) \ \)の特性方程式は三次方程式となる。制御系を安定にする\( \ K \ \)の条件をラウス・フルビッツの安定判別法を適用して求めよ。
【ワンポイント解説】
フィードバック制御系の安定判別に関する問題です。
伝達関数を求めてから安定判別をする典型的な問題です。
自動制御の問題は比較的パターン化されており,本問のように過去問の類題から出題されることも多いので,よく過去問を習熟するようにしましょう。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\hline
\end{array}
\]
2.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)
2次遅れの伝達関数\( \ W(s) \ \)の一般式は,減衰係数\( \ \zeta \ \),固有角周波数\( \ \omega _{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
W(s)&=&\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表されます。このとき\( \ \zeta \ \)において,
\[
\begin{eqnarray}
0≦\zeta <1のとき&:&応答が振動的となる \\[ 5pt ]
\zeta =1のとき&:&応答が振動しない限界 \\[ 5pt ]
\zeta >1のとき&:&応答が振動しない \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時,ラウスの安定判別法による安定条件は,
\[
\begin{eqnarray}
&&1. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
【解答】
(1)開ループ伝達関数\( \ \displaystyle G\left( s\right) =\frac {Y\left( s\right) }{E\left( s\right) } \ \)
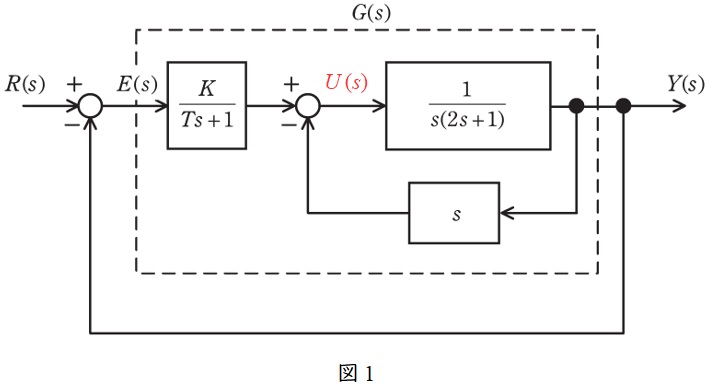
図1に示すように操作量\( \ U\left( s\right) \ \)を設定すると,
\[
\begin{eqnarray}
\frac {K}{Ts+1}E\left( s\right) -sY\left( s\right) &=&U\left( s\right) & ・・・・・・・・・・ ①& \\[ 5pt ]
\frac {1}{s\left( 2s+1\right) }U\left( s\right) &=&Y\left( s\right) & ・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となるので,①を②に代入して整理すると,
\[
\begin{eqnarray}
\frac {1}{s\left( 2s+1\right) }\left\{ \frac {K}{Ts+1}E\left( s\right) -sY\left( s\right) \right\} &=&Y\left( s\right) \\[ 5pt ]
\frac {K}{s\left( 2s+1\right) \left( Ts+1\right) }E\left( s\right) -\frac {1}{2s+1}Y\left( s\right) &=&Y\left( s\right) \\[ 5pt ]
Y\left( s\right) +\frac {1}{2s+1}Y\left( s\right) &=&\frac {K}{s\left( 2s+1\right) \left( Ts+1\right) }E\left( s\right) \\[ 5pt ]
\frac {2s+2}{2s+1}Y\left( s\right) &=&\frac {K}{s\left( 2s+1\right) \left( Ts+1\right) }E\left( s\right) \\[ 5pt ]
2\left( s+1\right) Y\left( s\right) &=&\frac {K}{s\left( Ts+1\right) }E\left( s\right) \\[ 5pt ]
\frac {Y\left( s\right) }{E\left( s\right) } &=&\frac {K}{2s\left( s+1\right) \left( Ts+1\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)閉ループ伝達関数\( \ \displaystyle W\left( s\right) =\frac {Y\left( s\right) }{R\left( s\right) } \ \)
問題図のフィードバック制御系において,
\[
\begin{eqnarray}
\left\{ R\left( s \right) -Y\left( s\right) \right\} G\left( s\right) &=&Y\left( s\right) \\[ 5pt ]
G\left( s\right) R\left( s \right) -G\left( s\right) Y\left( s\right) &=&Y\left( s\right) \\[ 5pt ]
\left\{ 1+G\left( s\right) \right\} Y\left( s\right) &=&G\left( s\right) R\left( s \right) \\[ 5pt ]
\frac { Y\left( s\right) }{R\left( s \right) } &=&\frac {G\left( s\right) }{1+G\left( s\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,(1)解答式を代入すると,
\[
\begin{eqnarray}
\frac { Y\left( s\right) }{R\left( s \right) } &=&\frac {\displaystyle \frac {K}{2s\left( s+1\right) \left( Ts+1\right) }}{\displaystyle 1+\frac {K}{2s\left( s+1\right) \left( Ts+1\right) }} \\[ 5pt ]
&=&\frac {\displaystyle \frac {K}{2s\left( s+1\right) \left( Ts+1\right) }}{\displaystyle \frac {2s\left( s+1\right) \left( Ts+1\right) +K}{2s\left( s+1\right) \left( Ts+1\right) }} \\[ 5pt ]
&=&\frac {\displaystyle K }{\displaystyle 2s\left( s+1\right) \left( Ts+1\right) +K} \\[ 5pt ]
&=&\frac {\displaystyle K }{\displaystyle 2Ts^{3}+2s^{2}+2Ts^{2}+2s+K} \\[ 5pt ]
&=&\frac {\displaystyle K }{\displaystyle 2Ts^{3}+\left( 2T+2\right) s^{2}+2s+K} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ T=0 \ \)としたとき,目標値のステップ状変化に対する制御量の時間応答\( \ y\left( t\right) \ \)が振動的となる\( \ K \ \)の条件
(2)解答式において\( \ T=0 \ \)とすると,
\[
\begin{eqnarray}
W\left( s\right) &=&\frac {\displaystyle K }{\displaystyle 2s^{2}+2s+K} \\[ 5pt ]
&=&\frac {\displaystyle 0.5K }{\displaystyle s^{2}+s+0.5K} \\[ 5pt ]
\end{eqnarray}
\]
となり,ワンポイント解説「2.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)」の通り,二次遅れ標準形と比較すると,
\[
\begin{eqnarray}
\omega _{\mathrm {n}}^{2} &=&0.5K ⇔ \omega _{\mathrm {n}}=\sqrt {0.5K} \\[ 5pt ]
2\zeta \omega _{\mathrm {n}}&=&1 \\[ 5pt ]
\zeta &=&\frac {1}{2\omega _{\mathrm {n}}} \\[ 5pt ]
&=&\frac {1}{2\sqrt {0.5K}} \\[ 5pt ]
&=&\frac {1}{\sqrt {2K}} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,振動的となる条件は,
\[
\begin{eqnarray}
0&≦& \zeta &<&1 \\[ 5pt ]
0&≦&\frac {1}{\sqrt {2K}} &<&1 \\[ 5pt ]
\end{eqnarray}
\]
ここで\( \ K>0 \ \)より,\( \ \displaystyle \frac {1}{\sqrt {2K}}>0 \ \)であるから,
\[
\begin{eqnarray}
\frac {1}{\sqrt {2K}} &<&1 \\[ 5pt ]
\sqrt {2K} &>&1 \\[ 5pt ]
2K &>&1 \\[ 5pt ]
K &>&0.5 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ K=1 \ \)としたとき,目標値の単位インパルス変化に対する制御量の時間応答\( \ y\left( t\right) \ \)
(2)解答式において\( \ T=0 \ \),\( \ K=1 \ \)を代入すると,
\[
\begin{eqnarray}
\frac { Y\left( s\right) }{R\left( s \right) } &=&\frac {\displaystyle 1 }{\displaystyle 2s^{2}+2s+1} \\[ 5pt ]
Y\left( s\right) &=&\frac {\displaystyle 1 }{\displaystyle 2s^{2}+2s+1}R\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.基本的なラプラス変換」の通り,単位インパルス関数のラプラス変換は\( \ 1 \ \)なので,\( \ R\left( s \right) =1 \ \)を代入すると,
\[
\begin{eqnarray}
Y\left( s\right) &=&\frac {\displaystyle 1 }{\displaystyle 2s^{2}+2s+1} \\[ 5pt ]
&=&\frac {0.5}{\displaystyle s^{2}+s+0.5} \\[ 5pt ]
&=&\frac {0.5}{\displaystyle \left( s+0.5\right) ^{2} +0.25} \\[ 5pt ]
&=&\frac {0.5}{\displaystyle \left( s+0.5\right) ^{2} +0.5^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「1.基本的なラプラス変換」及び\( \ \mathcal {L} \left[ \mathrm {e}^{-at}x\left( t \right) \right] =X\left( s+a\right) \ \)を用いて逆ラプラス変換すると,
\[
\begin{eqnarray}
y\left( t\right) &=&\mathrm {e}^{-0.5t} \sin 0.5t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ T=2 \ \)としたとき,制御系を安定にする\( \ K \ \)の条件
(2)解答式において\( \ T=2 \ \)とすると,
\[
\begin{eqnarray}
W\left( s\right) &=&\frac {\displaystyle K }{\displaystyle 4s^{3}+6 s^{2}+2s+K} \\[ 5pt ]
\end{eqnarray}
\]
となり,特性方程式は,\( \ 4s^{3}+6 s^{2}+2s+K=0 \ \)となる。ワンポイント解説「3.ラウスの安定判別法」の通り,ラウス表を作成すると,
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & 4 & 2 \\
2行 & 6 & K \\
3行 & \frac {6\times 2-4K}{6} & 0 \\
4行 & K & 0 \\
\end{array}
\]
となるので,安定であるための条件は,
\[
\begin{eqnarray}
\frac {6\times 2-4K}{6} &>&0 \\[ 5pt ]
12-4K &>&0 \\[ 5pt ]
K &<&3 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは