Contents
【問題】
【難易度】★★★★☆(やや難しい)
三相円筒形同期発電機を無限大母線に接続して運転する場合に関して,次の問に答えよ。ただし,無限大母線の電圧は同期機の定格電圧に等しく,同期機の定格皮相電力は\( \ 15 \ \mathrm {MV\cdot A} \ \),定格力率は遅れ\( \ 80 \ \mathrm {%} \ \),同期リアクタンス\( \ X_{\mathrm {s}} \ \)は\( \ 1.8 \ \mathrm {p.u.} \ \),また単位法は自己定格皮相電力及び自己定格電圧を基準とし,同期機の磁気飽和と損失は無視するものとする。
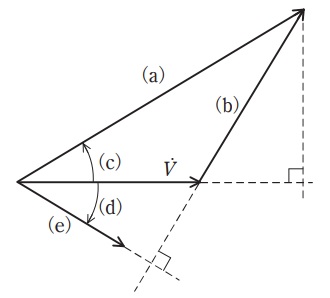
(1) この発電機を遅れ力率で運転したとき,端子電圧(相電圧)を\( \ V \ \mathrm {[p.u.]} \ \),無負荷誘導起電力を\( \ E \ \mathrm {[p.u.]} \ \),電流を\( \ I \ \mathrm {[p.u.]} \ \),負荷角を\( \ \delta \ \mathrm {[rad]} \ \),力率角を\( \ \theta \ \mathrm {[rad]} \ \),として,端子電圧のフェーザ\( \ \dot V \ \)を基準にしたフェーザ図は以下のようになった。このフェーザ図中の\( \ \left( \mathrm {a} \right) \ \),\( \ \left( \mathrm {b} \right) \ \),\( \ \left( \mathrm {c} \right) \ \),\( \ \left( \mathrm {d} \right) \ \),\( \ \left( \mathrm {e} \right) \ \)に当てはまる記号を答えよ。(解答例 \( \ \left( \mathrm {a} \right) \ \mathrm {j}X_{\mathrm {s}}\dot I \ \),\( \ \left( \mathrm {b} \right) \ \theta \ \) ,\( \ \left( \mathrm {c} \right) \ \dot I \ \),\( \ \cdots \ \))
(2) フェーザ図から無負荷誘導起電力\( \ E \ \mathrm {[p.u.]} \ \)を\( \ V \ \),\( \ I \ \),\( \ \theta \ \),及び\( \ X_{\mathrm {s}} \ \)で表す式を導出し,定格運転時における無負荷誘導起電力を\( \ E_{\mathrm {n}} \ \mathrm {[p.u.]} \ \)として,その値を求めよ。
(3) フェーザ図と有効電力\( \ P=VI\cos \theta \ \mathrm {[p.u.]} \ \)の式から,\( \ P \ \)を\( \ V \ \),\( \ E \ \),\( \ \delta \ \),及び\( \ X_{\mathrm {s}} \ \)で表す式を導出せよ。
(4) この発電機を定格運転した場合に,次の問に答えよ。
a) 定格運転時の負荷角を\( \ \delta _{\mathrm {n}} \ \)として,\( \ \sin \delta _{\mathrm {n}} \ \)の値を求めよ。
b) 小問(3)で求めた式の最大値が定態安定極限電力\( \ P_{\mathrm {m}} \ \mathrm {[p.u.]} \ \)である。この\( \ P_{\mathrm {m}} \ \)を表す式を示せ。また,定格運転時の定態安定極限電力を\( \ P_{\mathrm {mn}} \ \mathrm {[MW]} \ \)として,その値を求めよ。
(5) 定格運転中の発電機において,界磁電流を定格値の\( \ 80 \ \mathrm {%} \ \)に減少させた場合に,次の問に答えよ。
a) このときの発電機の定態安定極限電力\( \ P_{\mathrm {m}}^{\prime } \ \mathrm {[MW]} \ \)は定格運転時と比べて増加または減少するかいずれか答えよ。また,\( \ P_{\mathrm {m}}^{\prime } \ \)の値を求めよ。
b) このときの発電機の負荷角を\( \ \delta ^{\prime } \ \)として,\( \ \sin \delta ^{\prime } \ \)の値を求めよ。また,このときの発電機の定態安定度(同期安定性)は定格運転時と比べて向上又は低下するかいずれか答えよ。
【ワンポイント解説】
同期発電機の誘導起電力や電力,安定度に関する問題です。
一つ一つの設問はそれほど難解ではありませんが,問題数が多く\( \ 30 \ \)分で解くのはかなり厳しい問題でした。
練習問題としてはとても良い問題となりますので,ぜひ理解するようにして下さい。
1.同期発電機の等価回路
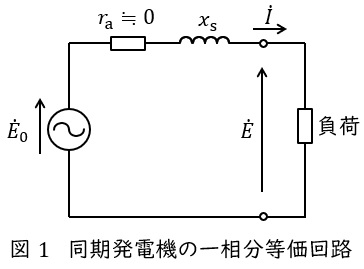
同期発電機の一相分等価回路は誘導起電力(相電圧)\( \ {\dot E}_{0} \ \mathrm {[V]} \ \),端子電圧(相電圧)\( \ \dot E \ \mathrm {[V]} \ \),同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)とすると,図1のようになります。
通常,電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は十分に小さいと考え,無視して考えることが一般的です。
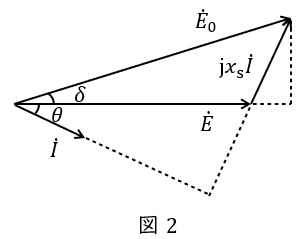
また,等価回路よりベクトル図は図2のようになります。
2.オーム法から単位法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ \mathrm {[\Omega ]} \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)フェーザ図中の\( \ \left( \mathrm {a} \right) \ \),\( \ \left( \mathrm {b} \right) \ \),\( \ \left( \mathrm {c} \right) \ \),\( \ \left( \mathrm {d} \right) \ \),\( \ \left( \mathrm {e} \right) \ \)に当てはまる記号
ワンポイント解説「1.同期発電機の等価回路」の通り,フェーザ図は図3のようになり,
\( \ \left( \mathrm {a} \right) \ \dot E \ \)
\( \ \left( \mathrm {b} \right) \ \mathrm {j}X_{\mathrm {s}}\dot I \ \)
\( \ \left( \mathrm {c} \right) \ \delta \ \)
\( \ \left( \mathrm {d} \right) \ \theta \ \)
\( \ \left( \mathrm {e} \right) \ \dot I \ \)
と求められる。
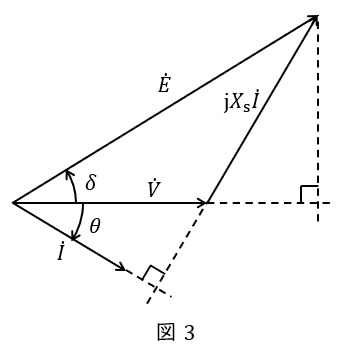
(2)\( \ E \ \mathrm {[p.u.]} \ \)を\( \ V \ \),\( \ I \ \),\( \ \theta \ \),及び\( \ X_{\mathrm {s}} \ \)で表す式,及び\( \ E_{\mathrm {n}} \ \mathrm {[p.u.]} \ \)の値
フェーザ図の図4に示す三角形に三平方の定理を適用すると,
\[
\begin{eqnarray}
E &=& \sqrt {\left( V+X_{\mathrm {s}}I\sin \theta \right) ^{2}+\left( X_{\mathrm {s}}I\cos \theta \right) ^{2}} \\[ 5pt ]
&=& \sqrt {V^{2}+2VX_{\mathrm {s}}I\sin \theta +\left( X_{\mathrm {s}}I\sin \theta \right) ^{2}+\left( X_{\mathrm {s}}I\cos \theta \right) ^{2}} \\[ 5pt ]
&=& \sqrt {V^{2}+2VX_{\mathrm {s}}I\sin \theta +\left( X_{\mathrm {s}}I\right) ^{2}\left( \sin ^{2}\theta +\cos ^{2}\theta \right) } \\[ 5pt ]
&=& \sqrt {V^{2}+2VX_{\mathrm {s}}I\sin \theta +\left( X_{\mathrm {s}}I\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,定格運転時における無負荷誘導起電力\( \ E_{\mathrm {n}} \ \mathrm {[p.u.]} \ \)は,負荷の\( \ \sin \theta \ \)が,
\[
\begin{eqnarray}
\sin \theta &=& \sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=& \sqrt {1-0.8 ^{2}} \\[ 5pt ]
&=& 0.6 \\[ 5pt ]
\end{eqnarray}
\]
であり,定格運転時は\( \ V_{\mathrm {n}}=1.0 \ \mathrm {[p.u.]} \ \),\( \ I_{\mathrm {n}}=1.0 \ \mathrm {[p.u.]} \ \)であるから,
\[
\begin{eqnarray}
E_{\mathrm {n}} &=& \sqrt {V_{\mathrm {n}}^{2}+2V_{\mathrm {n}}X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta +\left( X_{\mathrm {s}}I\right) ^{2}} \\[ 5pt ]
&=& \sqrt {1.0^{2}+2\times 1.0\times 1.8\times 1.0 \times 0.6 +\left( 1.8\times 1.0\right) ^{2}} \\[ 5pt ]
&≒& 2.5298 → 2.53 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
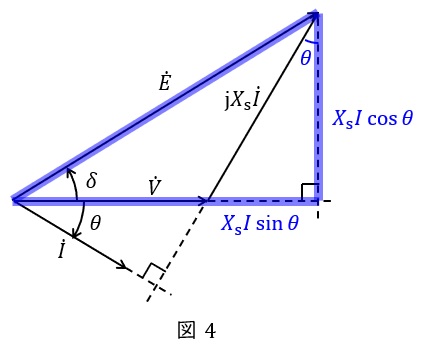
(3)\( \ P \ \)を\( \ V \ \),\( \ E \ \),\( \ \delta \ \),及び\( \ X_{\mathrm {s}} \ \)で表す式
図4において,
\[
\begin{eqnarray}
X_{\mathrm {s}}I\cos \theta &=& E\sin \delta \\[ 5pt ]
I\cos \theta &=& \frac {E\sin \delta }{X_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
P &=& VI\cos \theta \\[ 5pt ]
&=& V\cdot \frac {E\sin \delta }{X_{\mathrm {s}}} \\[ 5pt ]
&=& \frac {VE}{X_{\mathrm {s}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)a)\( \ \sin \delta _{\mathrm {n}} \ \)の値
(3)解答式を変形すると,
\[
\begin{eqnarray}
P &=& \frac {VE}{X_{\mathrm {s}}}\sin \delta \\[ 5pt ]
\sin \delta &=& \frac {PX_{\mathrm {s}}}{VE} \\[ 5pt ]
\end{eqnarray}
\]
であり,定格運転時の出力\( \ P_{\mathrm {n}} \ \mathrm {[p.u.]} \ \)は,定格皮相電力\( \ S_{\mathrm {n}}=15 \ \mathrm {[MV\cdot A]} \ \)を\( \ 1.0 \ \mathrm {[p.u.]} \ \)とするので,
\[
\begin{eqnarray}
P_{\mathrm {n}} &=& S_{\mathrm {n}}\cos \theta \\[ 5pt ]
&=& 1.0\times 0.8 \\[ 5pt ]
&=& 0.8 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,定格運転時の\( \ \sin \delta _{\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
\sin \delta _{\mathrm {n}}&=& \frac {P_{\mathrm {n}}X_{\mathrm {s}}}{V_{\mathrm {n}}E_{\mathrm {n}}} \\[ 5pt ]
&=& \frac {0.8\times 1.8}{1.0\times 2.5298} \\[ 5pt ]
&≒&0.56921 → 0.569 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)b)定態安定極限電力\( \ P_{\mathrm {m}} \ \mathrm {[p.u.]} \ \)と定格運転時の定態安定極限電力\( \ P_{\mathrm {mn}} \ \mathrm {[MW]} \ \)
同期発電機の同期化力は,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}\delta } &=& \frac {VE}{X_{\mathrm {s}}}\cos \delta \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta }>0 \ \)のとき安定なので,定態安定極限電力\( \ P_{\mathrm {m}} \ \mathrm {[p.u.]} \ \)は\( \ \displaystyle \delta =\frac {\pi }{2} \ \)のとき得られる。したがって,
\[
\begin{eqnarray}
P_{\mathrm {m}} &=& \frac {VE}{X_{\mathrm {s}}} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,定格運転時の定態安定極限電力\( \ P_{\mathrm {mn}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {mn}} \ \mathrm {[p.u.]} &=& \frac {V_{\mathrm {n}}E_{\mathrm {n}}}{X_{\mathrm {s}}} \\[ 5pt ]
&=& \frac {1.0\times 2.5298}{1.8} \\[ 5pt ]
&≒& 1.4054 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,\( \ P_{\mathrm {mn}} \ \mathrm {[MW]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {mn}} &=& P_{\mathrm {mn}} \ \mathrm {[p.u.]}\cdot S_{\mathrm {n}} \\[ 5pt ]
&=& 1.4054 \times 15 \\[ 5pt ]
&≒& 21.082 → 21.1 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(5)a)界磁電流を定格値の\( \ 80 \ \mathrm {%} \ \)に減少させた場合の定態安定極限電力\( \ P_{\mathrm {m}}^{\prime } \ \mathrm {[MW]} \ \)の定格運転時の定態安定極限電力\( \ P_{\mathrm {mn}} \ \mathrm {[MW]} \ \)との比較とその値
界磁電流を定格値の\( \ 80 \ \mathrm {%} \ \)に減少させた場合,誘導起電力が比例して低下するので,そのときの誘導起電力\( \ E^{\prime } \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
E^{\prime } &=& E_{\mathrm {n}}\times 0.8 \\[ 5pt ]
&=& 2.5298\times 0.8 \\[ 5pt ]
&≒& 2.0238 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,そのときの定態安定極限電力\( \ P_{\mathrm {m}}^{\prime } \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {m}}^{\prime } \ \mathrm {[p.u.]} &=& \frac {V_{\mathrm {n}}E^{\prime }}{X_{\mathrm {s}}} \\[ 5pt ]
&=& \frac {1.0\times 2.0238}{1.8} \\[ 5pt ]
&≒& 1.1243 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,\( \ P_{\mathrm {m}}^{\prime } \ \mathrm {[MW]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {m}}^{\prime } &=&P_{\mathrm {m}}^{\prime } \ \mathrm {[p.u.]}\cdot S_{\mathrm {n}} \\[ 5pt ]
&=& 1.1243 \times 15 \\[ 5pt ]
&≒& 16.865 → 16.9 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,定格運転時と比べて定態安定極限電力は低くなる。
(5)b)このときの発電機の\( \ \sin \delta ^{\prime } \ \)の値と発電機の定態安定度(同期安定性)は定格運転時と比べて向上又は低下するか
(4)a)と同様に,このときの発電機の\( \ \sin \delta ^{\prime } \ \)は,
\[
\begin{eqnarray}
\sin \delta ^{\prime }&=& \frac {P_{\mathrm {n}}X_{\mathrm {s}}}{V_{\mathrm {n}}E^{\prime }} \\[ 5pt ]
&=& \frac {0.8\times 1.8}{1.0\times 2.0238} \\[ 5pt ]
&≒&0.71153 → 0.712 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。このときの\( \ \sin \delta ^{\prime }=0.712 \ \)は定格運転時\( \ \sin \delta _{\mathrm {n}}=0.569 \ \)より大きいので,負荷角\( \ \delta ^{\prime } \ \)は定格運転時の負荷角\( \ \delta _{\mathrm {n}} \ \)より大きくなるから,定態安定度は定格運転時と比べて低下する。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは