Contents
【問題】
【難易度】★★★☆☆(普通)
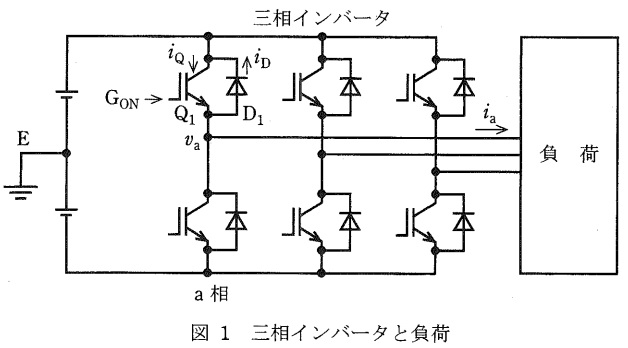
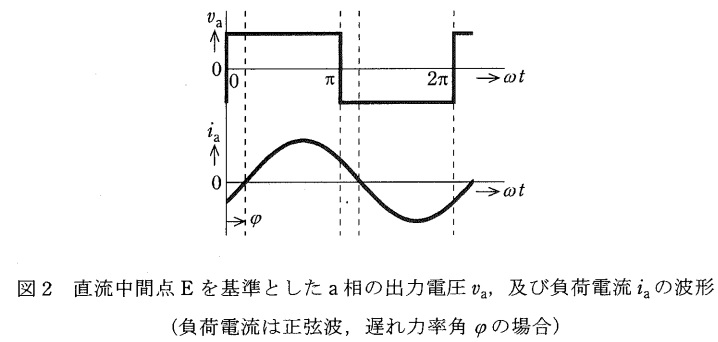
図1に示すように,三相\( \ \mathrm {IGBT} \ \)インバータで負荷に電流を供給する動作を考える。図2に直流中間点\( \ \mathrm {E} \ \)を基準とした\( \ \mathrm {a} \ \)相の出力電圧\( \ v_{\mathrm {a}} \ \),及び負荷電流\( \ i_{\mathrm {a}} \ \)の波形を示す。この図のように,インバータは\( \ 1 \ \)パルス運転でも負荷電流\( \ i_{\mathrm {a}} \ \)は正弦波とみなすことができるとする。このとき,次の問に答えよ。
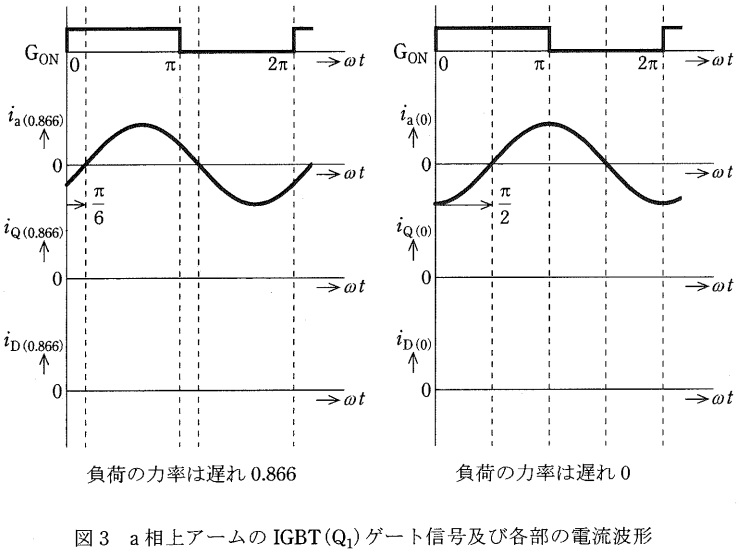
(1) 負荷の力率(基本波力率,以下同じ)が遅れ\( \ \displaystyle 0.866 \left( \cos \frac {\pi }{6} \right) \ \)及び遅れ\( \ \displaystyle 0 \left( \cos \frac {\pi }{2} \right) \ \)の二つの場合を考える。図3に示すように,\( \ \mathrm {a} \ \)相上アームの\( \ \mathrm {IGBT}\left( \mathrm {Q}_{1} \right) \ \)に与えられるゲート信号\( \ \mathrm {G_{ON}} \ \)のオンのタイミングに合わせて,\( \ \mathrm {a} \ \)相の負荷電流\( \ i_{\mathrm {a}\left( 0.866 \right) } \ \)及び\( \ i_{\mathrm {a}\left( 0 \right) } \ \)が流れる。このとき,図3と同じ図が答案用紙に印刷されているので,負荷力率が遅れ\( \ 0.866 \ \)及び遅れ\( \ 0 \ \)の場合に流れる\( \ \mathrm {IGBT}\left( \mathrm {Q}_{1} \right) \ \)及びその逆並列ダイオード\( \ \left( \mathrm {D}_{1} \right) \ \)の電流\( \ i_{\mathrm {Q}\left( 0.866 \right) } \ \),\( \ i_{\mathrm {D}\left( 0.866 \right) } \ \),\( \ i_{\mathrm {Q}\left( 0 \right) } \ \)及び\( \ i_{\mathrm {D}\left( 0 \right) } \ \)の波形を太線で明確に描け。
(2) \( \ \mathrm {a} \ \)相の負荷電流の実効値が\( \ 100 \ \mathrm {[A]} \ \)であったとする。負荷の力率が遅れ\( \ 0.866 \ \)の場合における\( \ \mathrm {IGBT}\left( \mathrm {Q}_{1} \right) \ \)電流の平均値\( \ I_{\mathrm {Q}\left( 0.866 \right) } \ \mathrm {[A]} \ \),及び負荷の力率が遅れ\( \ 0 \ \)の場合におけるダイオード\( \ \left( \mathrm {D}_{1} \right) \ \)電流の平均値\( \ I_{\mathrm {D}\left( 0 \right) } \ \mathrm {[A]} \ \)を求めよ。
【ワンポイント解説】
三相インバータに関する問題です。
難易度が高い年のパワーエレクトロニクスの問題に比べれば幾分取り組みやすい問題であったかなと思います。
インバータの動作を理解する上ではとても良い問題ですので,内容を理解するようにしましょう。
1.三相インバータの動作
三相インバータの動作は以下の通りとなります。まずは\( \ \mathrm {a} \ \)相の動作を理解すれば\( \ \mathrm {b} \ \)相,\( \ \mathrm {c} \ \)相も同様に考えることができます。
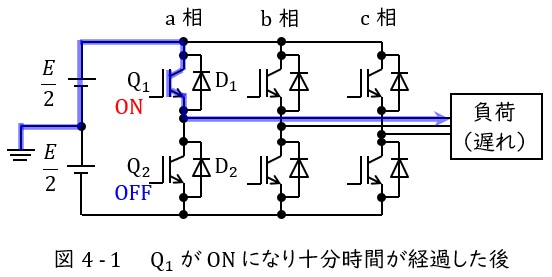
①\( \ \omega t=0 \ \mathrm {[rad]} \ \)で\( \ \mathrm {Q_{1}} \ \)が\( \ \mathrm {ON} \ \)になり十分に時間が経過した後
図4-1に示すように\( \ \displaystyle \frac {E}{2} \ \)→\( \ \mathrm {Q_{1}} \ \)→負荷と電流が流れます。
図4-1より出力端子の電圧は\( \ \displaystyle v_{\mathrm {a}}=\frac {E}{2} \ \)となり,出力電流\( \ i_{\mathrm {a}}>0 \ \)となります。
②\( \ \omega t=\pi \ \mathrm {[rad]} \ \)で\( \ \mathrm {Q_{2}} \ \)が\( \ \mathrm {ON} \ \)になった直後
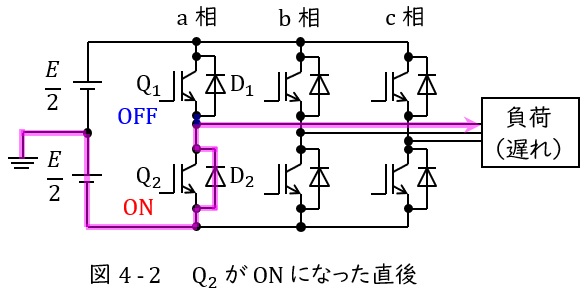
負荷のリアクタンスに蓄えられているエネルギーにより電流\( \ i_{\mathrm {a}}>0 \ \)が維持されるので,図4-2に示すように\( \ \displaystyle \frac {E}{2} \ \)→\( \ \mathrm {D_{2}} \ \)→負荷と電流が流れます。
図4-2より出力端子の電圧は\( \ \displaystyle v_{\mathrm {a}}=-\frac {E}{2} \ \)となり,出力電流\( \ i_{\mathrm {a}}>0 \ \)となります。
③\( \ \omega t=\pi \ \mathrm {[rad]} \ \)で\( \ \mathrm {Q_{2}} \ \)が\( \ \mathrm {ON} \ \)になり十分に時間が経過した後
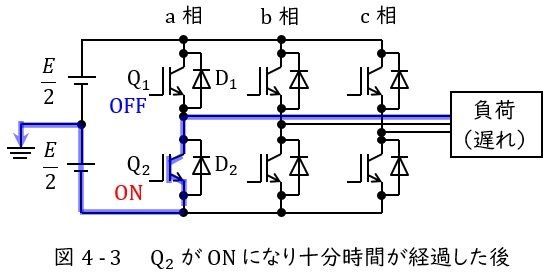
図4-3に示すように負荷→\( \ \mathrm {Q_{2}} \ \)→\( \ \displaystyle \frac {E}{2} \ \)と電流が流れます。
図4-3より出力端子の電圧は\( \ \displaystyle v_{\mathrm {a}}=-\frac {E}{2} \ \)となり,出力電流\( \ i_{\mathrm {a}}<0 \ \)となります。
④\( \ \omega t=0 \ \mathrm {[rad]} \ \)で\( \ \mathrm {Q_{1}} \ \)が\( \ \mathrm {ON} \ \)になった直後
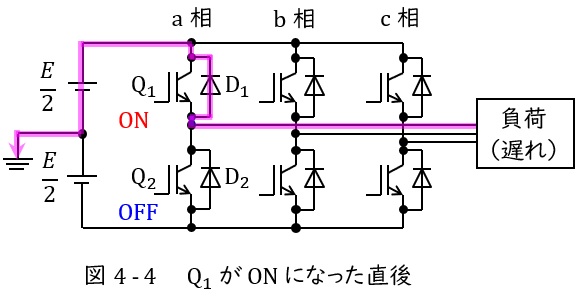
負荷のリアクタンスに蓄えられているエネルギーにより電流\( \ i_{\mathrm {a}}<0 \ \)が維持されるので,図4-4に示すように負荷→\( \ \mathrm {D_{1}} \ \)→\( \ \displaystyle \frac {E}{2} \ \)と電流が流れます。
図4-4より出力端子の電圧は\( \ \displaystyle v_{\mathrm {a}}=\frac {E}{2} \ \)となり,出力電流\( \ i_{\mathrm {a}}<0 \ \)となります。
以降①~④を繰り返します。
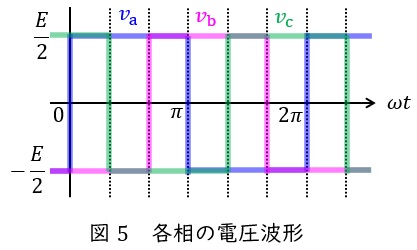
以上から,\( \ \mathrm {a} \ \)相においては,\( \ 0<\omega t≦ \pi \ \mathrm {[rad]} \ \)で\( \ \displaystyle v_{\mathrm {a}}=\frac {E}{2} \ \),\( \ \pi <\omega t≦ 2\pi \ \mathrm {[rad]} \ \)で\( \ \displaystyle v_{\mathrm {a}}=-\frac {E}{2} \ \)が出力され,\( \ \mathrm {b} \ \)相及び\( \ \mathrm {c} \ \)相においては\( \ \mathrm {a} \ \)相から順に\( \ \displaystyle \frac {2}{3}\pi \ \mathrm {[rad]} \ \)ずつ遅らせて動作させることで,図5に示すような三相の方形波が得られることになります。
2.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ T \ \)の周期関数であるとしたとき,平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
定義式は,
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{T}\int _{0}^{T}f( \theta ) \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これを正弦波\( \ v\left( t \right) =V_{\mathrm {m}}\sin \omega t \ \)に適用すると,
\[
\begin{eqnarray}
V_{\mathrm {av}} &=&\frac {1}{\pi }\int _{0}^{\pi }V_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {V_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ]
&=&\frac {V_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ]
&=&\frac {2}{\pi }V_{\mathrm {m}}
\end{eqnarray}
\]
となります。
②実効値\( \ F \ \)
定義式は,
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{T} \int _{0}^{T} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ]
\end{eqnarray}
\]
であり,これを正弦波\( \ v\left( t \right) =V_{\mathrm {m}}\sin \omega t \ \)に適用すると,
\[
\begin{eqnarray}
V &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{V_{\mathrm {m}}}^{2}\sin ^{2}\omega t \mathrm {d}\omega t} \\[ 5pt ]
&=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\int _{0}^{\pi }\frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ]
&=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\omega t -\frac {1}{4}\sin 2\omega t \right] _{0}^{\pi } } \\[ 5pt ]
&=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\pi -0 -0 +0 \right] _{0}^{\pi } } \\[ 5pt ]
&=&\frac {V_{\mathrm {m}}}{\sqrt {2}}
\end{eqnarray}
\]
となります。
【解答】
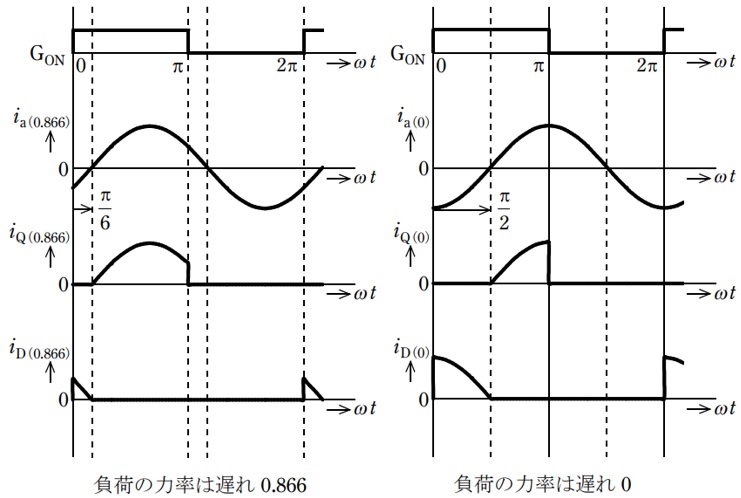
(1)\( \ i_{\mathrm {Q}\left( 0.866 \right) } \ \),\( \ i_{\mathrm {D}\left( 0.866 \right) } \ \),\( \ i_{\mathrm {Q}\left( 0 \right) } \ \)及び\( \ i_{\mathrm {D}\left( 0 \right) } \ \)の波形
ワンポイント解説「1.三相インバータの動作」の通り,\( \ i_{\mathrm {Q}\left( 0.866 \right) } \ \)及び\( \ i_{\mathrm {Q}\left( 0 \right) } \ \)はスイッチが切り替わってからしばらく時間が経過した後,\( \ i_{\mathrm {D}\left( 0.866 \right) } \ \)及び\( \ i_{\mathrm {D}\left( 0 \right) } \ \)はスイッチが切り替わった直後に流れる。それぞれの電流の向きに注意すると下図の通りとなる。
(2)\( \ I_{\mathrm {Q}\left( 0.866 \right) } \ \mathrm {[A]} \ \)及び\( \ I_{\mathrm {D}\left( 0 \right) } \ \mathrm {[A]} \ \)
題意より,\( \ \mathrm {a} \ \)相の負荷電流の実効値\( \ I_{\mathrm {a}}=100 \ \mathrm {[A]} \ \)であるため,その瞬時値\( \ i_{\mathrm {a}} \ \mathrm {[A]} \ \)は力率角を\( \ \theta \ \mathrm {[rad]} \ \)とすれば,
\[
\begin{eqnarray}
i_{\mathrm {a}}&=&\sqrt {2}I_{\mathrm {a}}\sin \left( \omega t-\theta \right) \\[ 5pt ]
&=&100\sqrt {2}\sin \left( \omega t-\theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となる。(1)解答より,\( \ i_{\mathrm {Q}\left( 0.866 \right) } \ \mathrm {[A]} \ \)は\( \ \displaystyle \frac {\pi }{6} \ \mathrm {[rad]} \ \)から\( \ \displaystyle \pi \ \mathrm {[rad]} \ \)まで導通し,その周期は\( \ \displaystyle 2\pi \ \mathrm {[rad]} \ \)であるからその平均値\( \ I_{\mathrm {Q}\left( 0.866 \right) } \ \mathrm {[A]} \ \)は,ワンポイント解説「2.平均値と実効値の定義」の通り,
\[
\begin{eqnarray}
I_{\mathrm {Q}\left( 0.866 \right) }&=&\frac {1}{2\pi } \int _{\frac {\pi }{6}}^{\pi } i_{\mathrm {a}} \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {1}{2\pi } \int _{\frac {\pi }{6}}^{\pi } 100\sqrt {2}\sin \left( \omega t-\frac {\pi }{6} \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \int _{\frac {\pi }{6}}^{\pi } \sin \left( \omega t-\frac {\pi }{6} \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left[ -\cos \left( \omega t-\frac {\pi }{6} \right) \right] _{\frac {\pi }{6}}^{\pi } \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left\{ -\cos \left( \pi -\frac {\pi }{6} \right) + \cos \left( \frac {\pi }{6} -\frac {\pi }{6} \right) \right\} \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left\{ -\cos \left( \frac {5\pi }{6} \right) + \cos 0 \right\} \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left( \frac {\sqrt{3}}{2}+1 \right) \\[ 5pt ]
&≒&42.0 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,(1)解答より,\( \ i_{\mathrm {D}\left( 0 \right) } \ \mathrm {[A]} \ \)は\( \ \displaystyle 0 \ \mathrm {[rad]} \ \)から\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)まで導通し,その周期は\( \ \displaystyle 2\pi \ \mathrm {[rad]} \ \)であるからその平均値\( \ I_{\mathrm {D}\left( 0 \right) } \ \mathrm {[A]} \ \)は符号に注意すると,ワンポイント解説「2.平均値と実効値の定義」の通り,
\[
\begin{eqnarray}
I_{\mathrm {D}\left( 0 \right) }&=&\frac {1}{2\pi } \int _{0}^{\frac {\pi }{2}} -i_{\mathrm {a}} \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {1}{2\pi } \int _{0}^{\frac {\pi }{2}} -100\sqrt {2}\sin \left( \omega t-\frac {\pi }{2} \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \int _{0}^{\frac {\pi }{2}} -\sin \left( \omega t-\frac {\pi }{2} \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left[ \cos \left( \omega t-\frac {\pi }{2} \right) \right] _{0}^{\frac {\pi }{2}} \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left\{ \cos \left( \frac {\pi }{2} -\frac {\pi }{2} \right) – \cos \left( 0 -\frac {\pi }{2} \right) \right\} \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left\{ \cos 0 – \cos \left( -\frac {\pi }{2} \right) \right\} \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left(1-0\right) \\[ 5pt ]
&≒&22.5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは