《理論》〈電子理論〉[H21:問8]演算増幅器を用いた増幅回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

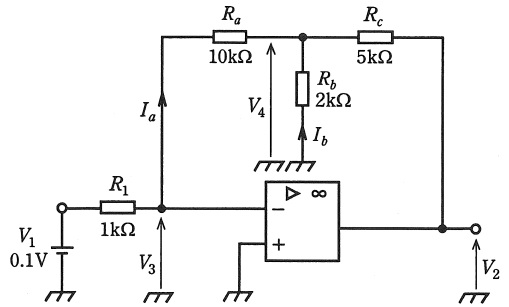
次の文章は，図に示す演算増幅器を用いた増幅回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる数値を解答群の中から選び，その記号をマークシートに記入しなさい。

図の増幅回路において，$ \ V_{1} \ $が$ \ 0.1 \ \mathrm {[V]} \ $のときの出力直流電圧$ \ V_{2} \ $を求める。まず，演算増幅器の性質から$ \ V_{3} \ $は$ \ \fbox {　（１）　} \ \mathrm {[V]} \ $であり，反転入力端子には電流は流れ込まない。このことから$ \ I_{a} \ $は$ \ \fbox {　（２）　} \ \mathrm {[mA]} \ $となる。したがって，$ \ V_{4} \ $は$ \ \fbox {　（３）　} \ \mathrm {[V]} \ $であり，$ \ I_{b} \ $が$ \ \fbox {　（４）　} \ \mathrm {[mA]} \ $であることがわかる。$ \ I_{a} \ $と$ \ I_{b} \ $の和が抵抗$ \ R_{c} \ $に流れるので$ \ V_{2} \ $は$ \ \fbox {　（５）　} \ \mathrm {[V]} \ $となる。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　2　　　　　&（ロ）&　10　　　　　&（ハ）&　0.5 \\[ 5pt ] &（ニ）&　0.1　　　　　&（ホ）&　-1　　　　　&（ヘ）&　1 \\[ 5pt ] &（ト）&　-5　　　　　&（チ）&　-4　　　　　&（リ）&　5 \\[ 5pt ] &（ヌ）&　-0.1　　　　　&（ル）&　0　　　　　&（ヲ）&　-0.5 \\[ 5pt ] &（ワ）&　0.2　　　　　&（カ）&　-10　　　　　&（ヨ）&　-0.2 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

演算増幅器を含む電子回路の計算問題です。
演算増幅器の問題は選択問題で出題されることがほとんどなので，必須の知識ではありませんが，パターンが決まっているものが多く計算量も少なめの問題が多いため，優先して選択しても良いかと思います。
本問も，演算増幅器の特性以外はキルヒホッフの法則で解ける問題です。

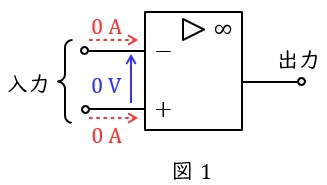
1.理想的な演算増幅器の特徴
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は$ \ 0 \ \mathrm {V} \ $（バーチャルショート）となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

【解答】

(1)解答：ル
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，演算増幅器の非反転入力端子（＋端子）が接地されているので，反転入力端子（－端子）の電位も$ \ 0 \ \mathrm {V} \ $となり，$ \ V_{3}=0 \ \mathrm {[V]} \ $と求められる。

(2)解答：ニ
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，演算増幅器の入力には電流が流れないので，$ \ I_{a} \ $は抵抗$ \ R_{1} \ $に流れる電流と等しく，
\[
\begin{eqnarray}
I_{a}&=&\frac {V_{1}-V_{3}}{R_{1}} \\[ 5pt ] &=&\frac {0.1-0}{1\times 10^{3}} \\[ 5pt ] &=&0.1\times 10^{-3} \ \mathrm {[A]}　→　0.1 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ホ
$ \ V_{4} \ $はキルヒホッフの法則より，
\[
\begin{eqnarray}
V_{4}&=&V_{3}-R_{a}I_{a} \\[ 5pt ] &=&0-10\times 10^{3}\times 0.1\times 10^{-3} \\[ 5pt ] &=&-1 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ハ
$ \ I_{b} \ $はキルヒホッフの法則より，電流の向きに注意すると，
\[
\begin{eqnarray}
I_{b}&=&\frac {-V_{4}}{R_{b}} \\[ 5pt ] &=&\frac {1}{2\times 10^{3}} \\[ 5pt ] &=&0.5\times 10^{-3} \ \mathrm {[A]}　→　0.5 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：チ
(2)及び(4)解答式より，抵抗$ \ R_{c} \ $に流れる電流$ \ I_{c} \ $は，
\[
\begin{eqnarray}
I_{c}&=&I_{a}+I_{b} \\[ 5pt ] &=&0.1\times 10^{-3}+0.5\times 10^{-3} \\[ 5pt ] &=&0.6\times 10^{-3} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，求める電圧$ \ V_{2} \ $はキルヒホッフの法則より，
\[
\begin{eqnarray}
V_{2}&=&V_{4}-R_{c}I_{c} \\[ 5pt ] &=&-1-5\times 10^{3}\times 0.6\times 10^{-3} \\[ 5pt ] &=&-4 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。