《理論》〈電子理論〉[H22:問7]pn接合で形成されるダイオードに関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，$ \ \mathrm {pn} \ $接合で形成されるダイオードに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる語句を解答群の中から選びなさい。

$ \ \mathrm {p} \ $層と$ \ \mathrm {n} \ $層とを接合させ，図のように電圧源$ \ E \ $を接続した。$ \ \mathrm {p} \ $層と$ \ \mathrm {n} \ $層との接合部には電子も正孔もほとんど存在しない$ \ \fbox {　（１）　} \ $と呼ばれる領域が生じる。まず電圧$ \ E=0 \ $とし，$ \ \mathrm {n} \ $層側の$ \ \fbox {　（１）　} \ $領域を考える。この領域では電子がなくなるため，電子を作り出した不純物であるドナーが$ \ \fbox {　（２）　} \ $となり，電子の流れに対して電位の障壁を作る。不純物分布が一様であるとすれば，$ \ \mathrm {n} \ $層の$ \ \fbox {　（１）　} \ $が始まる境界からの距離を$ \ x \ $とするとき，この障壁のポテンシャル関数は$ \ x \ $の$ \ \fbox {　（３）　} \ $関数として表される。

同様に$ \ \mathrm {p} \ $層側では正孔がなくなることで同様に電位の障壁を作る。この二つの障壁の高さの合計を拡散電位と呼んでいる。

電圧$ \ E \ $を正にすると，この二つの障壁の高さの合計は$ \ \fbox {　（４）　} \ $，電流が流れる。半導体中での電子や正孔の量はその運動エネルギーに対してボルツマン分布を持つと近似できるので，電流量は$ \ \mathrm {p} \ $層と$ \ \mathrm {n} \ $層間の電圧の増加に対して$ \ \fbox {　（５）　} \ $関数的に増加する。

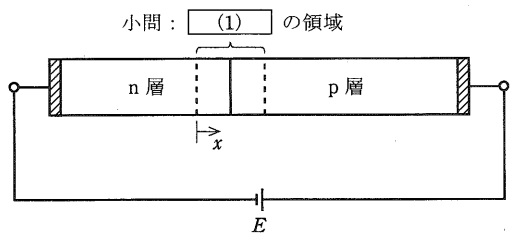
〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　負の電荷　　　　　　　&（ロ）&　空乏層　　　　　&（ハ）&　三　次 \\[ 5pt ] &（ニ）&　蓄積層　　　　　&（ホ）&　対　数　　　　　&（ヘ）&　正の電荷 \\[ 5pt ] &（ト）&　変化せず　　　　　&（チ）&　中性粒子　　　　　　　&（リ）&　指　数 \\[ 5pt ] &（ヌ）&　線　形　　　　　&（ル）&　低くなり　　　　　&（ヲ）&　正弦波 \\[ 5pt ] &（ワ）&　反転層　　　　　&（カ）&　二　次　　　　　&（ヨ）&　高くなり \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {pn} \ $接合ダイオードの特徴とその特性に関する問題です。
$ \ 3 \ $種ではまず出題されない範囲で，半導体工学の教科書に掲載されているような内容です。
もちろん詳しく数式の導出まで理解する必要はありませんが，その特性は理解しておくようにしましょう。

1.$ \ \mathrm {pn} \ $接合ダイオードにおける電荷の分布
図1のように$ \ \mathrm {p} \ $形半導体と$ \ \mathrm {n} \ $形半導体で$ \ \mathrm {pn} \ $接合すると，$ \ \mathrm {p} \ $形半導体の正孔が$ \ \mathrm {n} \ $形半導体に移動し，$ \ \mathrm {n} \ $形半導体中の電子と再結合し消滅します。すると，$ \ \mathrm {n} \ $形半導体中に正の電荷を持つ不純物がドーピングされることになります。
同様に$ \ \mathrm {n} \ $形半導体の自由電子が$ \ \mathrm {p} \ $形半導体に移動し，$ \ \mathrm {p} \ $形半導体中の正孔と再結合し消滅します。すると，$ \ \mathrm {p} \ $形半導体中に負の電荷を持つ不純物がドーピングされることになります。
したがって，これを繰り返すと図１の下のように$ \ \mathrm {n} \ $形半導体が＋で$ \ \mathrm {p} \ $形半導体が−となる空乏層ができ，その間には電界が発生することになります。

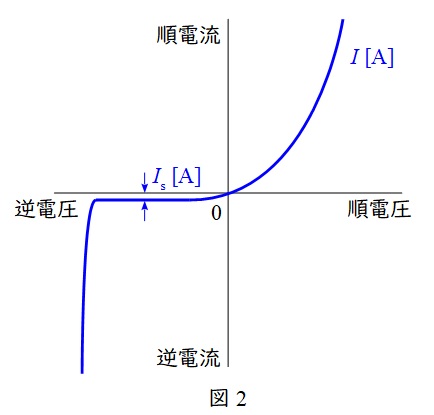
2.$ \ \mathrm {pn} \ $接合における順方向の電圧と電流の特性
$ \ \mathrm {pn} \ $接合における電圧と電流の特性は図2のようになり，一般に順方向の電圧$ \ V \ \mathrm {[V]} \ $と電流$ \ I \ \mathrm {[A]} \ $の間には，
\[
\begin{eqnarray}
I &=&I_{\mathrm {s}}\left( \mathrm {e}^{\frac {eV}{kT}}-1\right) \\[ 5pt ] \end{eqnarray}
\] となる関係があり，これをボルツマン分布近似といいます。ただし，$ \ I_{\mathrm {s}} \ \mathrm {[A]} \ $は逆方向飽和電流，$ \ k \ \mathrm {[J / K]} \ $はボルツマン定数，$ \ T \ \mathrm {[K]} \ $は絶対温度，$ \ e=1.602\times 10^{-19} \ \mathrm {[C]} \ $は電子の電荷です。

【解答】

(1)解答：ロ
題意より解答候補は，（ロ）空乏層，（ニ）蓄積層，（ワ）反転層，になると思います。
ワンポイント解説「1.$ \ \mathrm {pn} \ $接合ダイオードにおける電荷の分布」の通り，$ \ \mathrm {p} \ $層と$ \ \mathrm {n} \ $層の接合部の電子も正孔もほとんど存在しない層を空乏層といいます。

(2)解答：ヘ
題意より解答候補は，（イ）負の電荷，（ヘ）正の電荷，（チ）中性粒子，になると思います。
ワンポイント解説「1.$ \ \mathrm {pn} \ $接合ダイオードにおける電荷の分布」の通り，$ \ \mathrm {n} \ $層側では電子を作り出した不純物であるドナーが正の電荷となります。

(3)解答：カ
題意より解答候補は，（ハ）三次，（ホ）対数，（リ）指数，（ヌ）線形，（ヲ）正弦波，（カ）二次，になると思います。
空乏層内の電界は空乏層がはじまる部分が零であり$ \ \mathrm {pn} \ $接合部が最も大きくなります。したがって，空乏層内の不純物分布が一様であるとすれば，電界は線形に上昇していくため，電位は距離$ \ x $の二次関数として表されることになります。

(4)解答：ル
題意より解答候補は，（ト）変化せず，（ル）低くなり，（ヨ）高くなり，になると思います。
電圧$ \ E \ $を正にすると，この二つの障壁の高さは$ \ E \ $だけ低くなり，電流が流れます。

(5)解答：リ
題意より解答候補は，（ハ）三次，（ホ）対数，（リ）指数，（ヌ）線形，（ヲ）正弦波，（カ）二次，になると思います。
ワンポイント解説「2.$ \ \mathrm {pn} \ $接合における順方向の電圧と電流の特性」の通り，電流量は$ \ \mathrm {p} \ $層と$ \ \mathrm {n} \ $層間の電圧の増加に対しボルツマン分布を持つと近似できるので指数関数的に増加することになります。