【問題】
【難易度】★★★★★(難しい)
次の文章は,\( \ RLC \ \)回路の過渡現象とエネルギーに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
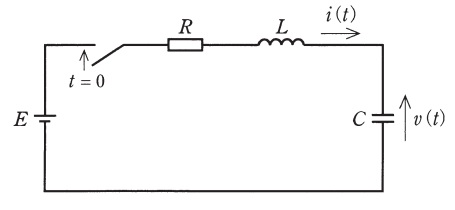
図に示す\( \ RLC \ \)直列回路を考える。ただし,\( \ t<0 \ \)では\( \ i\left( t \right) =0 \ \),\( \ v\left( t \right) =0 \ \)とする。\( \ t =0 \ \)でスイッチを閉じた。\( \ t≧0 \ \)での回路の電流\( \ i\left( t \right) \ \)と電圧\( \ v\left( t \right) \ \)の関係式は,
\[
\begin{eqnarray}
Ri\left( t \right) &=&E-\left[ \fbox { (1) } \ +v\left( t \right) \right] &・・・・・・・・・・ ①& \\[ 5pt ]
i\left( t \right) &=&\fbox { (2) } \ \times \frac {\mathrm {d}}{\mathrm {d}t}v\left( t \right) &・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となる。時刻\( \ t \ \left( t>0 \right) \ \)までに抵抗が消費するエネルギーを\( \ J_{\mathrm {R}}\left( t \right) \ \)で表すと
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( t \right) &=&\int _{0}^{t}i\left( \tau \right) Ri\left( \tau \right) \mathrm {d}\tau &・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ J_{\mathrm {R}}\left( t \right) \ \)は電流\( \ i\left( t \right) \ \)が零になるまで増加を続ける。①,②式を利用すると,
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( t \right) &=&\int _{0}^{t}i\left( \tau \right) Ri\left( \tau \right) \mathrm {d}\tau =\fbox { (3) } \ \times v\left( t \right) -\frac {1}{2}Li\left( t \right) ^{2}-\frac {1}{2}Cv\left( t \right) ^{2}&・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
となる。ただし,積分計算において微分の性質\( \ \displaystyle \frac {1}{2}\cdot \frac {\mathrm {d}}{\mathrm {d}t}\left[ x\left( t \right) ^{2} \right] =x\left( t \right) \frac {\mathrm {d}}{\mathrm {d}t} x\left( t \right) \ \)を利用している。④式の右辺でインダクタンスに蓄積されるエネルギーの引き算を省略した式を考えると,不等式
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( t \right) &≦&\fbox { (3) } \ \times v\left( t \right) -\frac {1}{2}Cv\left( t \right) ^{2}&・・・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
が成立する。⑤式は右辺は上に凸な\( \ v\left( t \right) \ \)の二次関数である。\( \ J_{\mathrm {R}}\left( t \right) >0 \ \)であることと⑤式により,この回路の過渡現象について次のことがいえる。電圧\( \ v\left( t \right) \ \)は絶対に\( \ \fbox { (4) }\times E \ \)以上になることはない。また負になることもない。④式に定常状態\( \ \left( t=\infty \right) \ \)での回路の電流\( \ i\left( \infty \right) \ \)と電圧\( \ v\left( \infty \right) \ \)の値を代入すると,\( \ J_{\mathrm {R}}\left( \infty \right) = \ \fbox { (5) } \ \)となる。\( \ t=\infty \ \)では⑤式の両辺は等号で結ばれる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 2 &(ロ)& CE^{2} &(ハ)& R \\[ 5pt ]
&(ニ)& L\frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) &(ホ)& L &(ヘ)& \frac {1}{2}CE \\[ 5pt ]
&(ト)& C &(チ)& \frac {1}{2} &(リ)& 2CE^{2} \\[ 5pt ]
&(ヌ)& 1 &(ル)& \frac {1}{2}CE^{2} &(ヲ)& RC\frac {\mathrm {d}}{\mathrm {d}t}v\left( t \right) \\[ 5pt ]
&(ワ)& CE &(カ)& \frac {1}{C}\int _{0}^{t}i\left( t \right) \mathrm {d}t &(ヨ)& 2CE \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
この問題は1種にも出題されそうな問題であり,過渡現象の知識はもちろんのこと,文章の読解,数学的なセンスも必要な問題となります。こういう問題は前半の空欄を間違えないことが大事となります。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ V_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ V_{\mathrm{L}} \ \),コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となり,電荷\( \ q \ \)との間に\( \ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ \)の関係があるので,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& R\frac {\mathrm {d}q}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {q}{C}
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ニ
ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」より,回路方程式は,
\[
\begin{eqnarray}
E&=Ri\left( t \right)+L\frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) +v\left( t \right) \\[ 5pt ]
Ri\left( t \right)&=E-\left[ L\frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right)+v\left( t \right) \right] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ト
ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」より,
\[
\begin{eqnarray}
v\left( t \right) &=& \frac {1}{C}\int i\left( t \right) \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となるので両辺微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}t}v\left( t \right) &=& \frac {1}{C}i\left( t \right) \\[ 5pt ]
i\left( t \right) &=& C\frac {\mathrm {d}}{\mathrm {d}t}v\left( t \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ワ
③に①を代入すると,
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( t \right) &=&\int _{0}^{t}i\left( \tau \right) Ri\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
&=&\int _{0}^{t}i\left( \tau \right) \left\{ E-\left[ L\frac {\mathrm {d}}{\mathrm {d}\tau }i\left( \tau \right) +v\left( \tau \right) \right] \right\} \mathrm {d}\tau \\[ 5pt ]
&=&\int _{0}^{t}\left\{ Ei\left( \tau \right) – i\left( \tau \right) \cdot L \frac {\mathrm {d}}{\mathrm {d}\tau }i\left( \tau \right) -v\left( \tau \right) i\left( \tau \right) \right\} \mathrm {d}\tau \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに②を代入すると,
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( t \right) &=&\int _{0}^{t}\left\{ CE\frac {\mathrm {d}}{\mathrm {d}\tau }v\left( \tau \right) – L i\left( \tau \right) \frac {\mathrm {d}}{\mathrm {d}\tau }i\left( \tau \right) -Cv\left( \tau \right) \frac {\mathrm {d}}{\mathrm {d}\tau }v\left( \tau \right) \right\} \mathrm {d}\tau \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,題意より\( \ \displaystyle \frac {1}{2}\cdot \frac {\mathrm {d}}{\mathrm {d}t}\left[ x\left( t \right) ^{2} \right] =x\left( t \right) \frac {\mathrm {d}}{\mathrm {d}t} x\left( t \right) \ \)の関係があるから,
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( t \right) &=&\int _{0}^{t}\left\{ CE\frac {\mathrm {d}}{\mathrm {d}\tau }v\left( \tau \right) – \frac {1}{2}L \frac {\mathrm {d}}{\mathrm {d}\tau }i\left( \tau \right) ^{2}-\frac {1}{2} C\frac {\mathrm {d}}{\mathrm {d}\tau }v\left( \tau \right) ^{2} \right\} \mathrm {d}\tau \\[ 5pt ]
&=& CEv\left( t \right) – \frac {1}{2}L i\left( t \right) ^{2}-\frac {1}{2} Cv\left( t \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:イ
④式を変形すると,
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( t \right) + \frac {1}{2}L i\left( t \right) ^{2}&=& CEv\left( t \right) -\frac {1}{2} Cv\left( t \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle \frac {1}{2}L i\left( t \right) ^{2}≧0 \ \)であるから,
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( t \right) &≦& CEv\left( t \right) -\frac {1}{2} Cv\left( t \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり⑤が成立する。ここで,\( \ \displaystyle f\left( t \right) =CEv\left( t \right) -\frac {1}{2} Cv\left( t \right) ^{2} \ \)とすると,
\[
\begin{eqnarray}
f\left( t \right) &=&-\frac {1}{2} Cv\left( t \right) ^{2}+CEv\left( t \right) \\[ 5pt ]
&=&-\frac {1}{2} C\left\{ v\left( t \right) ^{2}-2Ev\left( t \right) \right\} \\[ 5pt ]
&=&-\frac {1}{2} C\left[ \left\{ v\left( t \right) -E\right\} ^{2}-E^{2} \right] \\[ 5pt ]
&=&-\frac {1}{2} C\left\{ v\left( t \right) -E\right\} ^{2}+\frac {1}{2} CE^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle f\left( t \right) \ \)のグラフを描くと図1のようになる。
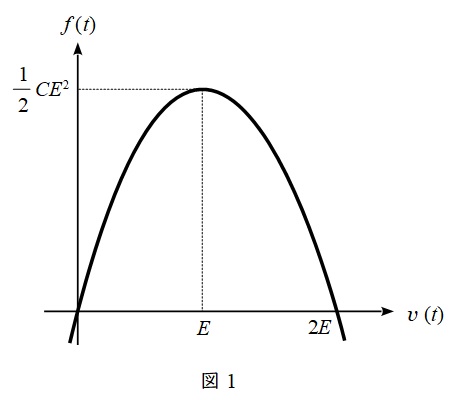
\( \ \displaystyle f\left( t \right) ≧J_{\mathrm {R}}\left( t \right) > 0 \ \)であるから,\( \ v \left( t \right) \ \)の取れる範囲は,\( \ 0 < v\left( t \right) < 2E \ \)となり,\( \ v \left( t \right) \ \)は絶対\( \ 2E \ \)以上になることはない。
(5)解答:ル
定常状態においては,リアクトル\( \ L \ \)の電圧降下がなくなり,コンデンサに電流が流れなくなるので,回路全体の電流も流れなくなるので,
\[
\begin{eqnarray}
v\left( \infty \right) &=&E \\[ 5pt ]
i\left( \infty \right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。これを④式に代入すると,
\[
\begin{eqnarray}
J_{\mathrm {R}}\left( \infty \right) &=& CEv\left( \infty \right) – \frac {1}{2}L i\left( \infty \right) ^{2}-\frac {1}{2} Cv\left( \infty \right) ^{2} \\[ 5pt ]
&=& CE^{2} – 0-\frac {1}{2} CE ^{2} \\[ 5pt ]
&=& \frac {1}{2} CE ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは