Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,微小ギャップを有する磁気回路に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選べ。
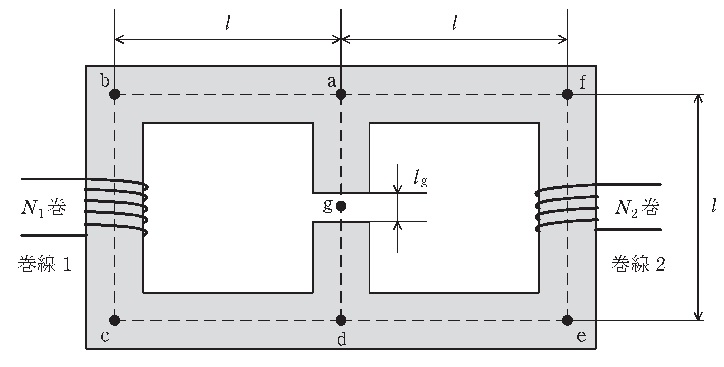
図のように,巻線\(1\)及び巻線\(2\)が鉄心に巻かれており,巻数はそれぞれ\(N_{1}\)及び\(N_{2}\)である。鉄心の断面は面積\(A\)の正方形で,磁束密度は断面内で一様に分布する。鉄心の断面の中心線を磁路として,その上に点\(\mathrm {a}~\mathrm {f}\)を取ると,四角形\(\mathrm {abcd}\)と四角形\(\mathrm {afed}\)は一辺\(l\)の正方形となる。ただし,\(l\)は鉄心の断面の一辺より十分大きい(\(l≫\sqrt {A}\))。ここで,\(\mathrm {a}-\mathrm {d}\)間に点\(\mathrm {g}\)を置き,長さ\(l_{\mathrm {g}}\)(\(l_{\mathrm {g}}≪\sqrt {A}\))の微小なギャップを設ける。
なお,鉄心の磁束の飽和やヒステリシス特性は無視でき,透磁率は\(\mu \)であるとして,磁束はギャップ部を除き全て鉄心中を通るものとする。また,ギャップ部の端効果は無視し,磁束は鉄心から連続して磁路と平行にギャップを通り抜けるものとし,ギャップの透磁率は\(\mu _{0}\)(\(\mu _{0}≪\mu \))であるとする。
点\(\mathrm {a}\)から点\(\mathrm {d}\)への磁路\(\mathrm {a}-\mathrm {g}-\mathrm {d}\)の磁気抵抗\(R\)は,鉄心部分の長さが\(l-l_{\mathrm {g}}\)であることを考慮すれば\(R=\fbox { (1) }\)であり,この\(R\)を,点\(\mathrm {a}\)から点\(\mathrm {b}\),\(\mathrm {c}\)を通り点\(\mathrm {d}\)に至る磁路\(\mathrm {a}-\mathrm {b}-\mathrm {c}-\mathrm {d}\)の磁気抵抗と同じにするようにギャップ長\(l_{\mathrm {g}}\)を決めると,\(l_{\mathrm {g}}=\fbox { (2) }\)である。このとき,巻線\(1\)のみに電流\(I_{1}\)を流すと,ギャップ中の磁束密度の大きさは\(R\)を用いて\(\fbox { (3) }\)と表せる。\(R\)を用いて巻線\(1\)の自己インダクタンス及び巻線\(1\)と\(2\)との間の相互インダクタンスを表すと,それぞれ\(\fbox { (4) }\),\(\fbox { (5) }\)である。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {N_{1}N_{2}}{3R} &(ロ)& \frac {\mu _{0}}{\mu -\mu _{0}}l &(ハ)& \frac {l-l_{\mathrm {g}}}{\mu A}+\frac {l_{\mathrm {g}}}{\mu _{0}A} \\[ 5pt ]
&(ニ)& \frac {N_{1}^{2}}{2R} &(ホ)& \frac {l}{\mu A}+\frac {l_{\mathrm {g}}}{\mu _{0}A} &(ヘ)& \frac {\left( N_{1}+N_{2}\right) ^{2}}{3R} \\[ 5pt ]
&(ト)& \frac {N_{2}}{3N_{1}R} &(チ)& \frac {N_{1}^{2}}{3R} &(リ)& \frac {N_{1}I_{1}}{3RA} \\[ 5pt ]
&(ヌ)& \frac {2N_{1}^{2}}{3R} &(ル)& \frac {N_{1}I_{1}}{2RA} &(ヲ)& \frac {3\mu _{0}}{\mu -\mu _{0}}l \\[ 5pt ]
&(ワ)& \frac {2N_{1}I_{1}}{3RA} &(カ)& \frac {4l-l_{\mathrm {g}}}{\mu A}+\frac {l_{\mathrm {g}}}{\mu _{0}A} &(ヨ)& \frac {2\mu _{0}}{\mu -\mu _{0}}l \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
磁気回路に関する問題です。ただ,私個人的には\(l≫\sqrt {A}\),\(l_{\mathrm {g}}≪\sqrt {A}\)さらには\(\mu _{0}≪\mu \)となっていて,解答では\(l-l_{\mathrm {g}}≒l\),\(\mu -\mu _{0}≒\mu \)としない計算には疑問を感じないでもないです。
1.磁気回路のオームの法則
中心長さ\(l\)の環状鉄心に巻き数\(N\)のコイルが巻かれ,そこに電流\(I\)が流れている時,鉄心内の磁界の強さ\(H\)は,アンペールの周回積分の法則より,
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ]
H&=&\frac {NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
であるから,鉄心内の磁束密度\(B\)は,鉄心内の透磁率\(\mu \)とすると,
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ]
&=&\frac {\mu NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
となる。鉄心内の磁束\(\phi \)は,鉄心の断面積\(S\)とすると,
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ]
&=&\frac {\mu NIS}{l} \\[ 5pt ]
&=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ]
\end{eqnarray}
\]
となり,起磁力\(F=NI\),磁気抵抗\(R_{\mathrm {m}}=\displaystyle \frac {l}{\mu S}\)とすると,磁気回路のオームの法則が成立します。

2.自己インダクタンス\(L\)
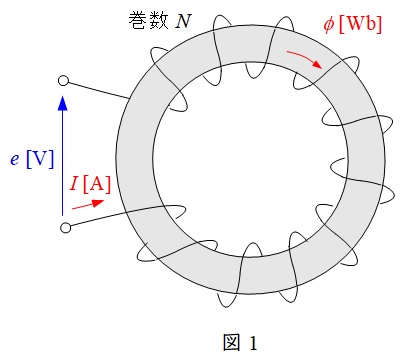
図1のような環状ソレノイド回路において,巻数\(N\)のコイルに電流\(I\)を流した時の鉄心の磁束\(\phi \)と比例定数\(L\)の関係は,起電力\(e\)を求める関係より,
\[
\begin{eqnarray}
-N\frac {\Delta \phi }{\Delta t}&=&-L\frac {\Delta I}{\Delta t} \\[ 5pt ]
N\phi &=&LI \\[ 5pt ]
L &=&\frac {N\phi }{I} \\[ 5pt ]
\end{eqnarray}
\]
となり,\(L\)を自己インダクタンスと言います。
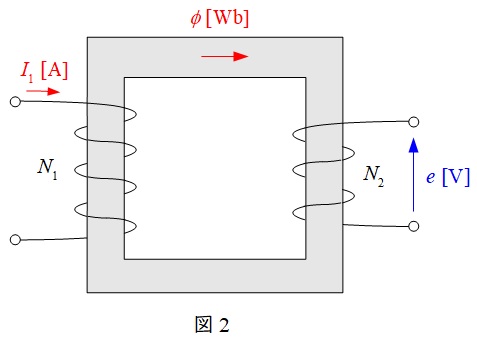
3.相互インダクタンス\(M\)
図2のような磁気回路において,巻数\(N_{1}\)側のコイルに電流\(I_{1}\)を流した時,巻数\(N_{2}\)側のコイルに発生する起電力\(\displaystyle e=-M\frac {\Delta I_{1}}{\Delta t}\)の比例定数\(M\)を相互インダクタンスと言い,起電力\(e\)に関する関係より,
\[
\begin{eqnarray}
-N_{2}\frac {\Delta \phi }{\Delta t}&=&-M\frac {\Delta I_{1}}{\Delta t} \\[ 5pt ]
N_{2}\phi &=&MI_{1} \\[ 5pt ]
M &=&\frac {N_{2}\phi }{I_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ハ
\(\mathrm {a}-\mathrm {g}-\mathrm {d}\)の磁気抵抗\(R\)は,鉄心部分の長さが\(l-l_{\mathrm {g}}\),ギャップ部の長さが\(l_{\mathrm {g}}\)であるから,
\[
\begin{eqnarray}
R &=&\frac {l-l_{\mathrm {g}}}{\mu A}+\frac {l_{\mathrm {g}}}{\mu _{0} A} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヨ
磁路\(\mathrm {a}-\mathrm {b}-\mathrm {c}-\mathrm {d}\)の磁気抵抗\(R_{1}\)は,
\[
\begin{eqnarray}
R_{1} &=&\frac {3l}{\mu A} \\[ 5pt ]
\end{eqnarray}
\]
であり,題意より\(R=R_{1}\)であるから,
\[
\begin{eqnarray}
\frac {l-l_{\mathrm {g}}}{\mu A}+\frac {l_{\mathrm {g}}}{\mu _{0} A} &=&\frac {3l}{\mu A} \\[ 5pt ]
\frac {l-l_{\mathrm {g}}}{\mu }+\frac {l_{\mathrm {g}}}{\mu _{0} } &=&\frac {3l}{\mu } \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺に\(\mu \mu _{0}\)を掛けて整理すると,
\[
\begin{eqnarray}
\mu_{0} \left( l-l_{\mathrm {g}}\right) + \mu l_{\mathrm {g}}&=&3\mu _{0}l \\[ 5pt ]
\left( \mu -\mu_{0}\right) l_{\mathrm {g}}&=&2\mu _{0}l \\[ 5pt ]
l_{\mathrm {g}}&=&\frac {2\mu _{0}}{\mu -\mu_{0}}l
\end{eqnarray}
\]
と求められる。
(3)解答:リ
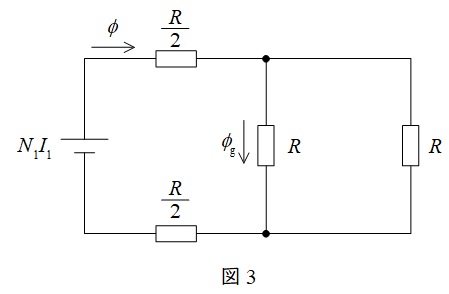
題意に沿って等価回路を描くと図3のようになる。
図1より,回路の合成抵抗\(R_{\mathrm {m}}\)は,
\[
\begin{eqnarray}
R_{\mathrm {m}}&=&\frac {R}{2}+\frac {R\cdot R}{R+R} +\frac {R}{2} \\[ 5pt ]
&=&\frac {3}{2}R \\[ 5pt ]
\end{eqnarray}
\]
であるから,巻線\(1\)を通過する磁束\(\phi \)は,ワンポイント解説「1.磁気回路のオームの法則」より,
\[
\begin{eqnarray}
\phi &=&\frac {N_{1}I_{1}}{R_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {2N_{1}I_{1}}{3R} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,ギャップ部を通過する磁束\(\phi _{\mathrm {g}} \)は\(\phi \)の半分であるから,
\[
\begin{eqnarray}
\phi _{\mathrm {g}} &=&\frac {1}{2}\phi \\[ 5pt ]
&=&\frac {1}{2}\times \frac {2N_{1}I_{1}}{3R} \\[ 5pt ]
&=&\frac {N_{1}I_{1}}{3R} \\[ 5pt ]
\end{eqnarray}
\]
となり,ギャップ部の磁束密度\(B _{\mathrm {g}} \)は,
\[
\begin{eqnarray}
B _{\mathrm {g}} &=&\frac {\phi _{\mathrm {g}}}{A} \\[ 5pt ]
&=&\frac {N_{1}I_{1}}{3RA} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヌ
ワンポイント解説「2.自己インダクタンス\(L\)」より,巻線\(1\)の自己インダクタンス\(L\)は,
\[
\begin{eqnarray}
L &=&\frac {N_{1}\phi }{I_{1}} \\[ 5pt ]
&=&\frac {\displaystyle N_{1}\frac {2N_{1}I_{1}}{3R} }{I_{1}} \\[ 5pt ]
&=&\frac {2N_{1}^{2}}{3R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:イ
巻線\(2\)側を通過する磁束\(\phi _{2}\)は\(\phi \)の半分であるから,
\[
\begin{eqnarray}
\phi _{2} &=&\frac {1}{2}\phi \\[ 5pt ]
&=&\frac {1}{2}\times \frac {2N_{1}I_{1}}{3R} \\[ 5pt ]
&=&\frac {N_{1}I_{1}}{3R} \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「3.相互インダクタンス\(M\)」より,相互インダクタンス\(M\)を求めると,
\[
\begin{eqnarray}
M &=&\frac {N_{2}\phi _{2}}{I_{1}} \\[ 5pt ]
&=&\frac {\displaystyle N_{2}\frac {N_{1}I_{1}}{3R}}{I_{1}} \\[ 5pt ]
&=&\frac {N_{1}N_{2}}{3R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは