Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,磁気回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
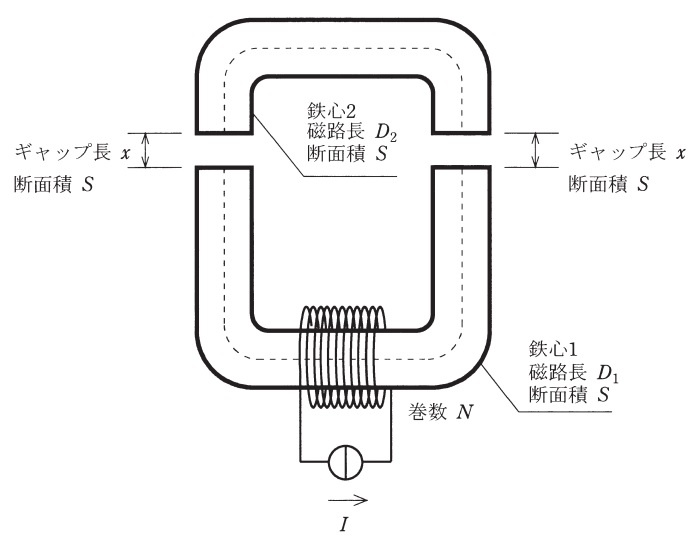
図は鉄心\( \ 1 \ \)と鉄心\( \ 2 \ \)からなる磁気回路の模式図である。鉄心\( \ 1 \ \)に巻数\( \ N \ \)のコイルが巻かれており,ここに電流\( \ I \ \mathrm {[A]} \ \)が流れている状況を考える。鉄心\( \ 2 \ \)は鉄心\( \ 1 \ \)と対向する位置に配置されており,その間のギャップ長を\( \ x \ \mathrm {[m]} \ \)とする。鉄心の断面積は場所によらず\( \ S \ \mathrm {[m^{2}]} \ \)とし,ギャップ部分の磁路の断面積も\( \ S \ \mathrm {[m^{2}]} \ \)とするとき,鉄心間の吸引力\( \ F \ \)を求めたい。なお,鉄心の透磁率を\( \ \mu _{1} \ \mathrm {[H/m]} \ \),ギャップ部分の透磁率を\( \ \mu _{0} \ \mathrm {[H/m]} \ \)とし,磁路において磁束は一様に分布し,漏れ磁束,磁気飽和,ヒステリシス,渦電流はないものとする。
鉄心及びギャップ部分の磁束密度を\( \ B \ \mathrm {[T]} \ \)とする。ここで,鉄心部分の磁路長の合計量を\( \ D=D_{1}+D_{2} \ \mathrm {[m]} \ \)とおいて,アンペールの周回積分の法則を用いることにより,磁束密度\( \ B \ \)と電流\( \ I \ \)の関係は,\( \ B=\fbox { (1) } \ \mathrm {[T]} \ \)と表される。
これを用いることで,コイルの自己インダクタンス\( \ L \ \)は,\( \ L=\fbox { (2) } \ \mathrm {[H]} \ \)と表される。さらに,この磁気回路に蓄えられている磁気エネルギー\( \ W_{\mathrm {m}} \ \)は\( \ L \ \)を用いると,\( \ W_{\mathrm {m}}=\fbox { (3) } \ \mathrm {[J]} \ \)と表される。よって,仮想変位の方法により,鉄心間の吸引力\( \ F \ \)を求めると,\( \ F=\fbox { (4) } \ \mathrm {[N]} \ \)と求めることができる。
通常\( \ \mu _{1} \ \)は\( \ \mu _{0} \ \)に比べて十分に大きいため,吸引力\( \ F \ \)は定性的には\( \ \fbox { (5) } \ \)すると言える。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {LI^{2}}{2\mu _{0}} &(ロ)& \frac {NI}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}} &(ハ)& \frac {LI^{2}}{2\mu _{1}} \\[ 5pt ]
&(ニ)& \frac {SN^{2}I^{2}}{\displaystyle 2x\left( \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}\right) } &(ホ)& \frac {\mu _{0}SN^{2}}{\displaystyle \frac {D}{\mu _{1}}+2x} &(ヘ)& \frac {\mu _{0}SN^{2}I^{2}}{4} \\[ 5pt ]
&(ト)& \frac {SN^{2}I^{2}}{\displaystyle \mu _{0}\left( \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}\right) ^{2}} &(チ)& \frac {LI^{2}}{2} &(リ)& \frac {SN^{2}}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}} \\[ 5pt ]
&(ヌ)& \frac {NI}{\displaystyle \frac {\mu _{1}}{D}+\frac {\mu _{0}}{2x}} &(ル)& \frac {2SN^{2}}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}} &(ヲ)& \frac {\mu _{0}NI}{\displaystyle \frac {D}{\mu _{1}}+2x} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ワ)& 電流 \ I \ に依存せず,ギャップ長 \ x \ の \ 2 \ 乗に反比例 \\[ 5pt ]
&(カ)& 電流 \ I \ の \ 2 \ 乗に比例し,ギャップ長 \ x \ に反比例 \\[ 5pt ]
&(ヨ)& 電流 \ I \ の \ 2 \ 乗に比例し,ギャップ長 \ x \ の \ 2 \ 乗に反比例 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
磁気回路に関する問題です。磁気回路の場合は電気回路より回路は易しい場合が多いので,慣れてしまえば得点しやすい問題であると言えると思います。(4)の計算がやや面倒なので難しめとしています。
1.磁気回路のオームの法則
中心長さ\( \ l \ \)の環状鉄心に巻き数\( \ N \ \)のコイルが巻かれ,そこに電流\( \ I \ \)が流れている時,鉄心内の磁界の強さ\( \ H \ \)は,アンペールの周回積分の法則より,
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ]
H&=&\frac {NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
であるから,鉄心内の磁束密度\( \ B \ \)は,鉄心内の透磁率\( \ \mu \ \)とすると,
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ]
&=&\frac {\mu NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
となる。鉄心内の磁束\( \ \phi \ \)は,鉄心の断面積\( \ S \ \)とすると,
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ]
&=&\frac {\mu NIS}{l} \\[ 5pt ]
&=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ]
\end{eqnarray}
\]
となり,起磁力\( \ F=NI \ \),磁気抵抗\( \ R_{\mathrm {m}}=\displaystyle \frac {l}{\mu S} \ \)とすると,磁気回路のオームの法則が成立します。

2.自己インダクタンス\( \ L \ \)
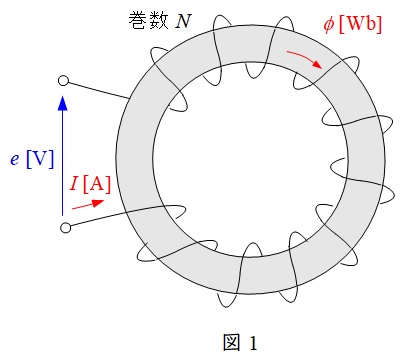
図1のような環状ソレノイド回路において,巻数\( \ N \ \)のコイルに電流\( \ I \ \)を流した時の鉄心の磁束\( \ \phi \ \)と比例定数\( \ L \ \)の関係は,起電力\( \ e \ \)を求める関係より,
\[
\begin{eqnarray}
-N\frac {\Delta \phi }{\Delta t}&=&-L\frac {\Delta I}{\Delta t} \\[ 5pt ]
N\phi &=&LI \\[ 5pt ]
L &=&\frac {N\phi }{I} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ L \ \)を自己インダクタンスと言います。
【解答】
(1)解答:ロ
鉄心内及びギャップ部の磁界の大きさを\( \ H_{1} \ \)及び\( \ H_{0} \ \)とすると,アンペールの法則より,
\[
\begin{eqnarray}
NI&=&H_{1}D_{1}+H_{1}D_{2}+H_{0}\cdot 2x \\[ 5pt ]
&=&H_{1}\left( D_{1}+D_{2}\right) +2H_{0}x \\[ 5pt ]
&=&H_{1}D +2H_{0}x \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ B=\mu _{1}H_{1}=\mu _{0}H_{0} \ \)の関係があるため,
\[
\begin{eqnarray}
NI&=&\frac {B}{\mu _{1}}\cdot D+2\cdot \frac {B}{\mu _{0}}\cdot x \\[ 5pt ]
&=&B\left( \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}\right) \\[ 5pt ]
B&=&\frac {NI}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[別解]
問題図の磁気回路において,ワンポイント解説「1.磁気回路のオームの法則」より,起磁力\( \ F^{\prime } \ \),磁気抵抗\( \ R_{\mathrm {m}} \ \)は,
\[
\begin{eqnarray}
F^{\prime }&=&NI \\[ 5pt ]
R_{\mathrm {m}}&=&\frac {D}{\mu _{1}S}+\frac {2x}{\mu _{0}S} \\[ 5pt ]
\end{eqnarray}
\]
であるから,磁気回路のオームの法則より回路の磁束\( \ \phi \ \)は,
\[
\begin{eqnarray}
\phi &=&\frac {F^{\prime }}{R_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {NI}{\displaystyle \frac {D}{\mu _{1}S}+\frac {2x}{\mu _{0}S}} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \phi =BS \ \)の関係より,磁束密度\( \ B \ \)の大きさは,
\[
\begin{eqnarray}
B &=&\frac {\phi }{S} \\[ 5pt ]
&=&\frac {NI}{\displaystyle \frac {D}{\mu _{1}S}+\frac {2x}{\mu _{0}S}}\cdot \frac {1}{S} \\[ 5pt ]
&=&\frac {NI}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:リ
ワンポイント解説「2.自己インダクタンス\( \ L \ \)」より,
\[
\begin{eqnarray}
L &=&\frac {N\phi }{I} \\[ 5pt ]
&=&\frac {NBS}{I} \\[ 5pt ]
&=&\frac {NS}{I}\cdot \frac {NI}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}} \\[ 5pt ]
&=&\frac {SN^{2}}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:チ
磁気回路に蓄えられるエネルギー\( \ W_{\mathrm {m}} \ \)は\( \ L \ \)を用いると,\( \ W_{\mathrm {m}}=\displaystyle \frac {1}{2}LI^{2} \ \)で求められる。
(4)解答:ト
磁気回路に蓄えられるエネルギー\( \ W_{\mathrm {m}} \ \)は,各値を代入すると,
\[
\begin{eqnarray}
W_{\mathrm {m}}&=&\frac {1}{2}LI^{2} \\[ 5pt ]
&=&\frac {1}{2}\frac {SN^{2}}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}}I^{2} \\[ 5pt ]
&=&\frac {1}{2}\frac {SN^{2}I^{2}}{\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,仮想変位において,鉄心\( \ 1 \ \)と鉄心\( \ 2 \ \)の間の吸引力は,\( \ \displaystyle F=-\frac {\mathrm {d}W_{\mathrm {m}}}{\mathrm {d}x} \ \)の関係があるから,\( \ A=\displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}} \ \)とおくと,
\[
\begin{eqnarray}
F&=&-\frac {\mathrm {d}W_{\mathrm {m}}}{\mathrm {d}x} \\[ 5pt ]
&=&-\frac {\mathrm {d}W_{\mathrm {m}}}{\mathrm {d}A}\cdot \frac {\mathrm {d}A}{\mathrm {d}x} \\[ 5pt ]
&=&\frac {1}{2}\frac {SN^{2}I^{2}}{A^{2}}\cdot \frac {2}{\mu _{0}} \\[ 5pt ]
&=&\frac {1}{2}\frac {SN^{2}I^{2}}{\left( \displaystyle \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}\right) ^{2}}\cdot \frac {2}{\mu _{0}} \\[ 5pt ]
&=&\frac {SN^{2}I^{2}}{\displaystyle \mu _{0}\left( \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
\( \ \mu _{1} ≫ \mu _{0} \ \)すなわち\( \displaystyle \ \frac {1}{\mu _{1}} ≪ \frac {1}{\mu _{0}} \ \)であるから,(4)の解答式は,
\[
\begin{eqnarray}
F&=&\frac {SN^{2}I^{2}}{\displaystyle \mu _{0}\left( \frac {D}{\mu _{1}}+\frac {2x}{\mu _{0}}\right) ^{2}} \\[ 5pt ]
&≃&\frac {SN^{2}I^{2}}{\displaystyle \mu _{0}\left( \frac {2x}{\mu _{0}}\right) ^{2}} \\[ 5pt ]
&=&\frac {SN^{2}I^{2}}{\displaystyle \frac {4x^{2}}{\mu _{0}}} \\[ 5pt ]
&=&\frac {\mu _{0}SN^{2}I^{2}}{4x^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,電流\( \ I \ \)の\( \ 2 \ \)乗に比例し,ギャップ長\( \ x \ \)の\( \ 2 \ \)乗に反比例する。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは