《理論》〈電子理論〉[H26:問8]演算増幅器における発振回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，図1に示す発振回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。ただし，演算増幅器には正の値の直流電圧源$ \ V_{\mathrm {DD}} \ $と負の値の直流電圧源$ \ -V_{\mathrm {SS}} \ $が接続されており，演算増幅器の特性は図2に示すとおり，$ \ V_{1}-V_{2} \ $が正のとき演算増幅器の出力電圧$ \ V_{\mathrm {out}} \ $は$ \ V_{\mathrm {DD}} \ $に等しく，$ \ V_{1}-V_{2} \ $が負のとき$ \ -V_{\mathrm {SS}} \ $に等しいとする。

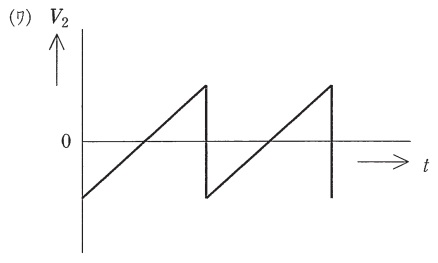
図1の回路において，初期状態として$ \ V_{\mathrm {out}} \ $が$ \ V_{\mathrm {DD}} \ $に等しく，$ \ V_{2} \ $が$ \ 0 \ \mathrm {V} \ $である場合を考える。このとき，抵抗$ \ R \ $を介してコンデンサ$ \ C \ $が充電され，$ \ V_{2} \ $が増加する。$ \ V_{2} \ $が$ \ \fbox {　（１）　} \ $を超えると，$ \ V_{\mathrm {out}} \ $は$ \ \fbox {　（２）　} \ $となる。このため，今度は抵抗$ \ R \ $を介してコンデンサ$ \ C \ $が放電され，$ \ V_{2} \ $が減少する。やがて，$ \ V_{2} \ $が$ \ \fbox {　（３）　} \ $を下回ると，$ \ V_{\mathrm {out}} \ $が$ \ \fbox {　（４）　} \ $に等しくなる。この動作が繰り返され，図1の回路は発振する。図1の回路が安定して発振している状態における$ \ V_{2} \ $の時間的変化を表す図は$ \ \fbox {　（５）　} \ $である。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　-2V_{\mathrm {SS}}　　　&（ロ）&　\frac {-R_{\mathrm {a}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}V_{\mathrm {SS}} 　　　&（ハ）&　\frac {-R_{\mathrm {a}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}\left( V_{\mathrm {DD}}+V_{\mathrm {SS}}\right) \\[ 5pt ] &（ニ）&　V_{\mathrm {DD}}　　　&（ホ）&　-V_{\mathrm {SS}} 　　　&（ヘ）&　-V_{\mathrm {DD}} \\[ 5pt ] &（ト）&　\frac {R_{\mathrm {b}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}\left( V_{\mathrm {DD}}-V_{\mathrm {SS}}\right)　　　&（チ）&　\frac {-R_{\mathrm {b}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}V_{\mathrm {SS}}　　　　&（リ）&　2V_{\mathrm {DD}} \\[ 5pt ] &（ヌ）&　\frac {R_{\mathrm {b}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}V_{\mathrm {DD}}　　　&（ル）&　\frac {R_{\mathrm {a}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}V_{\mathrm {DD}}　　　&（ヲ）&　V_{\mathrm {SS}} \\[ 5pt ] \end{eqnarray}
\] 　

【ワンポイント解説】

演算増幅器の特性を熟知していることは前提として，さらに電圧がどのようになるかといった，パワーエレクトロニクスのような論理的理解を必要とする問題となっています。理解してしまえば計算も易しい問題ですが，単純な分余計に受験生を惑わせてしまうかもしれません。試験本番ではよっぽど自信がなければ問7にした方が無難と思います。

1.理想的な演算増幅器の特徴
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は$ \ 0 \ \mathrm {V} \ $(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

※　ただし，本問の場合は１．入力端子間の電圧は零ではなく，特性が問題で与えられています。

【解答】

(1)解答：ル
(2)解答：ホ
$ \ V_{\mathrm {out}}=V_{\mathrm {DD}} \ $の時，$ \ V_{1} \ $の電圧は，
\[
\begin{eqnarray}
V_{1} &=& \frac {R_{\mathrm {a}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}V_{\mathrm {DD}} \\[ 5pt ] \end{eqnarray}
\] である。$ \ V_{2} \ $にはコンデンサの充電電圧がかかるので，初期状態から徐々に電圧が上昇し，$ \ V_{2} ＞ V_{1} \ $となると，出力電圧が$ \ -V_{\mathrm {SS}} \ $となります。
したがって，
\[
\begin{eqnarray}
V_{2} &＞& V_{1} \\[ 5pt ] V_{2} &＞& \frac {R_{\mathrm {a}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}V_{\mathrm {DD}} \\[ 5pt ] \end{eqnarray}
\] となると$ \ V_{\mathrm {out}} \ $が$ \ -V_{\mathrm {SS}} \ $になります。

(3)解答：ロ
(4)解答：ニ
(1)，(2)と同様に，$ \ V_{\mathrm {out}}=-V_{\mathrm {SS}} \ $の時，$ \ V_{1} \ $の電圧は，
\[
\begin{eqnarray}
V_{1} &=& \frac {-R_{\mathrm {a}}}{R_{\mathrm {a}}+R_{\mathrm {b}}}V_{\mathrm {SS}} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ V_{2} \ $にはコンデンサの充電電圧がかかるので，初期状態から徐々に電圧が減少し，$ \ V_{2} ＜ V_{1} \ $となると，出力電圧が$ \ V_{\mathrm {DD}} \ $となります。

(5)解答：ヨ
(1)～(4)の通り，$ \ V_{\mathrm {out}}=V_{\mathrm {DD}} \ $と$ \ V_{\mathrm {out}}=-V_{\mathrm {SS}} \ $が切り替わると$ \ V_{2} \ $の電圧が徐々に変化する特性があります。よって，$ \ V_{2} \ $の特性は(ヨ)となります。