Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,抵抗の測定に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選べ。
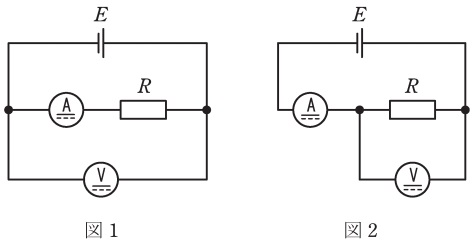
図1及び図2は,直流電圧源\( \ E \ \),内部抵抗\( \ r_{\mathrm {v}} \ \)の直流電圧計及び内部抵抗\( \ r_{\mathrm {c}} \ \)の直流電流計を用い,未知の抵抗\( \ R \ \)を測定する回路である。
図1において電圧計の指示が\( \ V_{1} \ \),電流計の指示が\( \ I_{1} \ \)であるとき,計器の指示から求められる抵抗を\( \ R_{1} \ \)とすると,\(\displaystyle R_{1}=\frac {V_{1}}{I_{1}}=\fbox { (1) }\)となる。次に,図2において電圧計の指示が\( \ V_{2} \ \),電流計の指示が\( \ I_{2} \ \)であるとき,計器の指示から求められる抵抗を\( \ R_{2} \ \)とすると,\(\displaystyle R_{2}=\frac {V_{2}}{I_{2}}=\fbox { (2) }\)となる。
測定の誤差率\( \ \varepsilon \ \)を\(\displaystyle \frac {測定値-真値}{真値}\)と定義すると,図1の測定における誤差率\( \ \varepsilon _{1} \ \)は,\( \ \varepsilon _{1}=\fbox { (3) }\),図2の測定における誤差率\( \ \varepsilon _{2} \ \)は,\( \ \varepsilon _{2}=\fbox { (4) }\)となる。
一般に,高抵抗を測定する場合には図1の回路が用いられ,\( \ R \ \)と\( \ r_{\mathrm {c}} \ \)の関係が\(\fbox { (5) }\)を満足する電流計を使用することにより,誤差が小さい測定が可能となる。
〔問8の解答群〕
\[
\begin{eqnarray}
&(イ)& r_{\mathrm {c}}-R &(ロ)& r_{\mathrm {v}} &(ハ)& R≫r_{\mathrm {c}} \\[ 5pt ]
&(ニ)& \frac {r_{\mathrm {v}}+r_{\mathrm {c}}}{r_{\mathrm {v}}+R} &(ホ)& -\frac {R}{r_{\mathrm {v}}+R} &(ヘ)& \frac {r_{\mathrm {v}}R}{r_{\mathrm {v}}+R} \\[ 5pt ]
&(ト)& r_{\mathrm {c}} &(チ)& R≪r_{\mathrm {c}} &(リ)& r_{\mathrm {c}}+\frac {r_{\mathrm {v}}R}{r_{\mathrm {v}}+R} \\[ 5pt ]
&(ヌ)& \frac {r_{\mathrm {v}}\left( r_{\mathrm {c}}+R\right) }{r_{\mathrm {c}}+r_{\mathrm {v}}+R} &(ル)& r_{\mathrm {c}}+R &(ヲ)& \frac {r_{\mathrm {c}}}{R} \\[ 5pt ]
&(ワ)& R=r_{\mathrm {c}} &(カ)& -\frac {r_{\mathrm {v}}}{R} &(ヨ)& R-r_{\mathrm {v}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
抵抗の測定に関する問題となっていますが,ほぼ電気回路の問題と言えると思います。(1),(2)の等式を立てる箇所が本問の肝となると思います。等価回路を描きよく整理して解くようにしましょう。
【解答】
(1)解答:ル
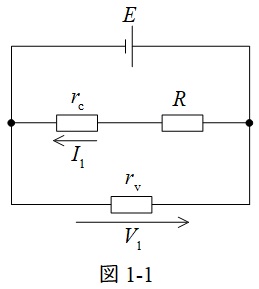
題意に沿って等価回路を描くと図1-1のようになる。
図1-1より,\( \ r_{\mathrm {c}} \ \)及び\( \ R \ \)の電圧降下の和が\( \ V_{1} \ \)と等しいから,
\[
\begin{eqnarray}
V_{1}&=&\left( r_{\mathrm {c}}+R\right) I_{1} \\[ 5pt ]
\frac {V_{1}}{I_{1}}&=&r_{\mathrm {c}}+R \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
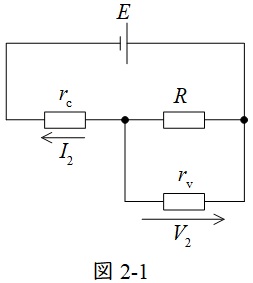
(2)解答:ヘ
題意に沿って等価回路を描くと図2-1のようになる。
\( \ r_{\mathrm {v}} \ \)を流れる電流について,オームの法則及び分流の法則より等式を立てると,
\[
\begin{eqnarray}
\frac {V_{2}}{r_{\mathrm {v}}}&=&\frac {R}{r_{\mathrm {v}}+R} I_{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係が成り立つから上式を整理すると,
\[
\begin{eqnarray}
\frac {V_{2}}{I_{2}}&=&\frac {r_{\mathrm {v}}R}{r_{\mathrm {v}}+R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヲ
本測定における真値は\( \ R \ \)であるから,誤差率\( \ \varepsilon _{1} \ \)は,
\[
\begin{eqnarray}
\varepsilon _{1}&=&\frac {R_{1} -R}{R} \\[ 5pt ]
&=&\frac {\left( r_{\mathrm {c}}+R\right) -R}{R} \\[ 5pt ]
&=&\frac {r_{\mathrm {c}}}{R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ホ
(3)と同様に,誤差率\( \ \varepsilon _{2} \ \)は,
\[
\begin{eqnarray}
\varepsilon _{2}&=&\frac {R_{2} -R}{R} \\[ 5pt ]
&=&\frac {\displaystyle \left( \frac {r_{\mathrm {v}}R}{r_{\mathrm {v}}+R} \right) -R}{R} \\[ 5pt ]
&=&\frac {r_{\mathrm {v}}R-R\left( r_{\mathrm {v}}+R\right) }{R\left( r_{\mathrm {v}}+R\right) } \\[ 5pt ]
&=&\frac {-R^{2}}{R\left( r_{\mathrm {v}}+R\right) } \\[ 5pt ]
&=&-\frac {R}{r_{\mathrm {v}}+R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ハ
(3)より,誤差率\( \ \displaystyle \varepsilon _{1}=\frac {r_{\mathrm {c}}}{R}\ \)を小さくなるためには\(R≫r_{\mathrm {c}}\)とすれば良い。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは