《理論》〈電気回路〉[R06:問3]閉回路同士が接続された直列回路に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，直流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

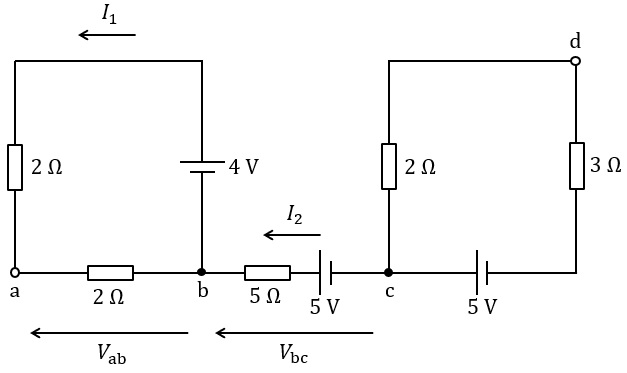
図に示すような直流電圧源及び抵抗から構成される回路を考える。ただし，回路の電圧・電流は，図の矢印の向きを正とする。

この回路において，点\( \ \mathrm {b} \ \)における電流則を踏まえれば，電流\( \ I_{1}= \ \fbox {　 （１） 　} \ \mathrm {A} \ \)，電流\( \ I_{2}= \ \fbox {　 （２） 　} \ \mathrm {A} \ \)である。また，点\( \ \mathrm {a} \ \)及び点\( \ \mathrm {b} \ \)間の電圧\( \ V_{\mathrm {ab}}= \ \fbox {　 （３） 　} \ \mathrm {V} \ \)，点\( \ \mathrm {b} \ \)及び点\( \ \mathrm {c} \ \)間の電圧\( \ V_{\mathrm {bc}}= \ \fbox {　 （４） 　} \ \mathrm {V} \ \)であり，点\( \ \mathrm {a} \ \)及び点\( \ \mathrm {d} \ \)間の電圧の大きさ\( \ \left| V_{\mathrm {ad}} \right| = \ \fbox {　 （５） 　} \ \mathrm {V} \ \)である。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　-3　　　　　&（ロ）&　-2　　　　　&（ハ）&　-1 \\[ 5pt ] &（ニ）&　0　　　　　&（ホ）&　1　　　　　&（ヘ）&　2 \\[ 5pt ] &（ト）&　3　　　　　&（チ）&　4　　　　　&（リ）&　5 \\[ 5pt ] &（ヌ）&　6　　　　　&（ル）&　7　　　　　&（ヲ）&　8 \\[ 5pt ] &（ワ）&　9　　　　　&（カ）&　10　　　　　&（ヨ）&　11 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

閉回路同士を接続した直流回路の電流値及び電圧値を求める問題です。
扱う公式等は基本的な内容であり，考え方も難しくありませんが，試験本番で出題されると「本当に良いだろうか」と焦ってしまう印象の問題です。
法則や原理，公式に従って導き出した答えは正しいと信じて解くようにして下さい。

1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが，法則を説明できる必要はなく，計算で使いこなせることが重要です。
①第1法則（電流則）
　回路の接続点に流入する電流の和と流出する電流の和が等しい。

　図1で言えば，例えば接続点\( \ \mathrm {A} \ \)において，
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ] \end{eqnarray}
\] 　となります。

②第2法則（電圧則）
　任意の閉回路において，起電力の総和と抵抗の電圧降下の和は等しい。

　図1で言えば，例えば閉回路\( \ 1 \ \)において，
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ] \end{eqnarray}
\] 　となります。

【解答】

(1)解答：ホ
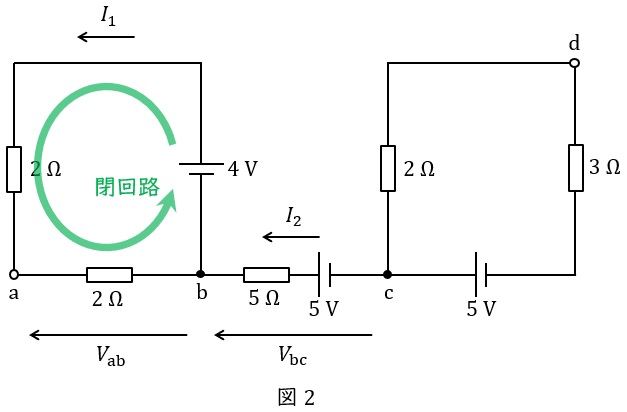
図2に示す閉回路にキルヒホッフの法則の電圧則を適用すると，ワンポイント解説「1.キルヒホッフの法則」の通り，
\[
\begin{eqnarray}
4 &=&2I_{1}+2I_{1} \\[ 5pt ] 4I_{1} &=&4 \\[ 5pt ] I_{1} &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ニ
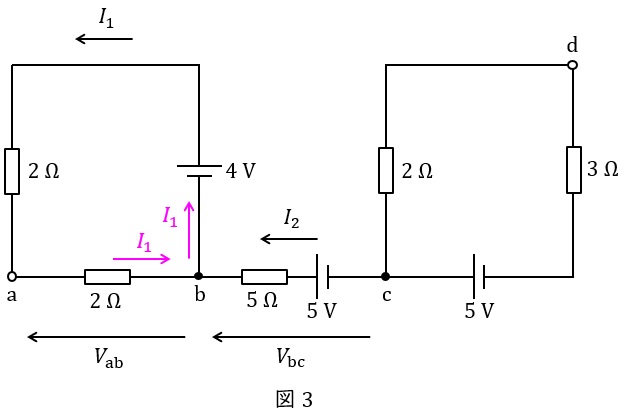
図3に示すように点\( \ \mathrm {b} \ \)における流入する電流と流出する電流の関係を考えれば，
\[
\begin{eqnarray}
I_{1}+I_{2}&=&I_{1} \\[ 5pt ] I_{2}&=&0 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヘ
点\( \ \mathrm {a} \ \)及び点\( \ \mathrm {b} \ \)間の電圧\( \ V_{\mathrm {ab}} \ \mathrm {[V]} \ \)は，\( \ I_{1} =1 \ \mathrm {[A]} \ \)なので，
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&2I_{1} \\[ 5pt ] &=&2\times 1 \\[ 5pt ] &=&2 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：リ
点\( \ \mathrm {b} \ \)及び点\( \ \mathrm {c} \ \)間の電圧\( \ V_{\mathrm {bc}} \ \mathrm {[V]} \ \)は，\( \ I_{2} =0 \ \mathrm {[A]} \ \)であるから，ワンポイント解説「1.キルヒホッフの法則」の通り，
\[
\begin{eqnarray}
V_{\mathrm {bc}} &=&5-5I_{2} \\[ 5pt ] &=&5-5\times 0 \\[ 5pt ] &=&5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

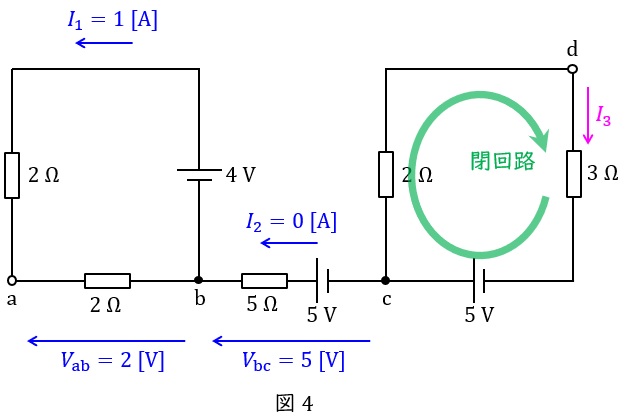
(5)解答：ワ
図4に示す閉回路にキルヒホッフの法則の電圧則を適用すると\( \ 3 \ \mathrm {\Omega } \ \)の抵抗に流れる電流\( \ I_{3} \ \mathrm {[A]} \ \)は，ワンポイント解説「1.キルヒホッフの法則」の通り，
\[
\begin{eqnarray}
5 &=&2I_{3}+3I_{3} \\[ 5pt ] 5I_{3} &=&5 \\[ 5pt ] I_{3} &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，点\( \ \mathrm {a} \ \)及び点\( \ \mathrm {d} \ \)間の電圧\( \ V_{\mathrm {ad}} \ \mathrm {[V]} \ \)は，ワンポイント解説「1.キルヒホッフの法則」の通り，
\[
\begin{eqnarray}
V_{\mathrm {ad}}&=&V_{\mathrm {ab}}+V_{\mathrm {bc}}+5-3I_{3} \\[ 5pt ] &=&2+5+5-3\times 1 \\[ 5pt ] &=&9 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。