《理論》〈電磁気〉[R07:問2]回転するコイルの相互インダクタンスに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，回転するコイルの相互インダクタンスに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

自己インダクタンスがそれぞれ$ \ L_{1} \ $，$ \ L_{2} \ $のコイル$ \ 1 \ $とコイル$ \ 2 \ $がある。コイル$ \ 1 \ $は固定されている一方で，コイル$ \ 2 \ $は回転するようになっており，回転角が$ \ \theta \ $であるときの相互インダクタンスは，$ \ M_{0}\cos \theta \ $で表せるものとする。ただし，$ \ M_{0} \ $は定数である。このとき，$ \ L_{1} \ $，$ \ L_{2} \ $，$ \ M_{0} \ $の間には一般に$ \ \fbox {　（１）　} \ $の関係が成り立つ。

コイル$ \ 1 \ $には定電流$ \ I_{1} \ $が，コイル$ \ 2 \ $には定電流$ \ I_{2} \ $が流れている。このとき，空間に蓄えられた合計の磁気エネルギー$ \ W \ $は$ \ \fbox {　（２）　} \ $である。

コイル$ \ 2 \ $の回転軸周りに発生するトルクは，仮想変位法の考え方に従って$ \ \displaystyle \frac{ \partial W }{ \partial \theta } \ $で求められ，それを計算すると，$ \ \fbox {　（３）　} \ $となる。

さらに，時刻を$ \ t \ $とし，コイル$ \ 2 \ $を$ \ \theta =\omega t \ $に従って角速度$ \ \omega \ $で定速回転させると，コイル$ \ 1 \ $に鎖交する磁束$ \ \mathit {\Phi }_{1} \ $は$ \ \fbox {　（４）　} \ $であり，ファラデーの電磁誘導の法則によりコイル$ \ 1 \ $に発生する起電力は$ \ \fbox {　（５）　} \ $となる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　L_{1}I_{1}+M_{0}I_{2}\cos \omega t　　　　　&（ロ）&　\omega \left( L_{1}+L_{2}\right) \left( I_{1}+I_{2}\right) \sin \omega t \\[ 5pt ] &（ハ）&　\frac {1}{2}\left( L_{1}+L_{2}\right) \left( I_{1}+I_{2}\right) ^{2}+M_{0}I_{1}I_{2}\cos \theta　　　　　&（ニ）&　\frac {1}{2}\frac {L_{1}L_{2}\sin \theta}{M_{0}\cos ^{2}\theta }I_{1}I_{2} \\[ 5pt ] &（ホ）&　L_{2}I_{2}+M_{0}I_{1}\cos \omega t　　　　　&（ヘ）&　\left( L_{1}+L_{2}\right) \left( I_{1}+I_{2}\right) \cos \omega t \\[ 5pt ] &（ト）&　L_{1}+L_{2}≧M_{0} 　　　　&（チ）&　-M_{0}I_{1}I_{2}\sin \theta \\[ 5pt ] &（リ）&　L_{1}L_{2}≧2{M_{0}}^{2} 　　　　　&（ヌ）&　\omega M_{0}I_{1}\sin \omega t \\[ 5pt ] &（ル）&　-M_{0}I_{1}I_{2}\cos \theta 　　　　&（ヲ）&　L_{1}L_{2}≧{M_{0}}^{2} \\[ 5pt ] &（ワ）&　\frac {1}{2}L_{1}{I_{1}}^{2}+\frac {1}{2}L_{2}{I_{2}}^{2}+M_{0}I_{1}I_{2}\cos \theta 　　　　&（カ）&　\frac {1}{2}\frac {L_{1}L_{2}}{M_{0}\cos \theta }I_{1}I_{2} \\[ 5pt ] &（ヨ）&　\omega M_{0}I_{2}\sin \omega t && \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

回転するコイルを用いた電磁誘導に関する問題です。
電験ではあまり出題されてこなかったパターンの問題で，ファラデーの電磁誘導の法則や微分積分をしっかり扱えるかが問われています。
一方できちんと理解していれば完答も狙える問題であるため，点数差が拡がりやすい問題といえるでしょう。

1.ファラデーの電磁誘導の法則と自己インダクタンス$ \ L \ $
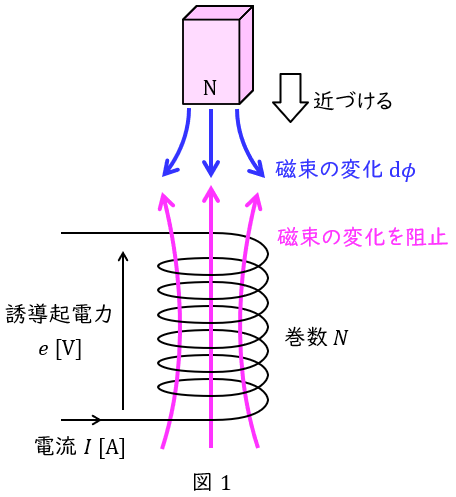
図1に示すように，巻数$ \ N \ $のコイルを貫通する磁束$ \ \phi \ \mathrm {[Wb]} \ $があるとき，コイルに発生する誘導起電力$ \ e \ \mathrm {[V]} \ $は，磁束の時間変化$ \ \displaystyle \frac {\mathrm {d} \phi }{\mathrm {d} t} \ $に比例し，
\[
\begin{eqnarray}
e&=&−N\frac {\mathrm {d} \phi }{\mathrm {d} t} \\[ 5pt ] \end{eqnarray}
\] で求められます。これをファラデーの電磁誘導の法則といいます。一方，電流変化$ \ \displaystyle \frac {\mathrm {d} I }{\mathrm {d} t} \ $を考える場合，
\[
\begin{eqnarray}
e&=&−L\frac {\mathrm {d} I }{\mathrm {d} t} \\[ 5pt ] \end{eqnarray}
\] という関係も成り立ち，$ \ L \ \mathrm {[H]}\ $を自己インダクタンスと言います。これらの関係から，
\[
\begin{eqnarray}
−N\frac {\mathrm {d} \phi }{\mathrm {d} t}&=&−L\frac {\mathrm {d} I }{\mathrm {d} t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。

2.相互インダクタンス$ \ M \ $
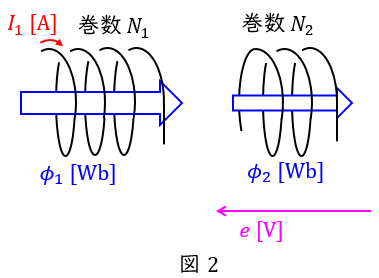
図2に示すように巻数$ \ N_{1} \ $と$ \ N_{2} \ $のコイルがあり，$ \ N_{1} \ $のコイルを流れる電流$ \ I_{1} \ \mathrm {[A]} \ $が変化したとすると，コイルを貫く磁束$ \ \phi _{1} \ \mathrm {[Wb]} \ $も変化し，一部の磁束は$ \ N_{2} \ $のコイルも貫くため，$ \ N_{2} \ $のコイルを貫く磁束$ \ \phi _{2} \ \mathrm {[Wb]} \ $も変化します。このとき，$ \ N_{2} \ $のコイルに発生する誘導起電力$ \ e \ \mathrm {[V]} \ $は，
\[
\begin{eqnarray}
e&=&−N_{2}\frac {\mathrm {d} \phi _{2}}{\mathrm {d} t} \\[ 5pt ] \end{eqnarray}
\] となります。また，$ \ N_{1} \ $のコイルの電流変化で考える場合は，
\[
\begin{eqnarray}
e&=&−M\frac {\mathrm {d} I_{1}}{\mathrm {d} t} \\[ 5pt ] \end{eqnarray}
\] という関係となり，$ \ M \ \mathrm {[H]}\ $を相互インダクタンスと言います。これらの関係から，
\[
\begin{eqnarray}
−N_{2}\frac {\mathrm {d} \phi _{2}}{\mathrm {d} t}&=&−M\frac {\mathrm {d} I_{1} }{\mathrm {d} t} \\[ 5pt ] N_{2}\phi _{2}&=&MI_{1} \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。

3.自己インダクタンスと相互インダクタンスの関係
自己インダクタンス$ \ L_{1} \ \mathrm {[H]} \ $と$ \ L_{2} \ \mathrm {[H]} \ $のコイルがある時の相互インダクタンス$ \ M \ \mathrm {[H]} \ $は，
\[
\begin{eqnarray}
M&=&k\sqrt {L_{1}L_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。この時，$ \ k \ $は結合係数と呼ばれ，$ \ 0≦k≦1 \ $となります。

4.二つのコイルに蓄えられるエネルギー$ \ W \ $
二つのコイルの自己インダクタンスが$ \ L_{1} \ \mathrm {[H]} \ $と$ \ L_{2} \ \mathrm {[H]} \ $，相互インダクタンスが$ \ M \ \mathrm {[H]} \ $であり，それぞれに電流$ \ I_{1} \ \mathrm {[A]} \ $及び$ \ I_{2} \ \mathrm {[A]} \ $が流れているとき，蓄えられるエネルギー$ \ W \ \mathrm {[J]} \ $は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}L_{1}{I_{1}}^{2}+\frac {1}{2}L_{2}{I_{2}}^{2}+MI_{1}I_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヲ
ワンポイント解説「3.自己インダクタンスと相互インダクタンスの関係」の通り，$ \ M_{0}≦\sqrt {L_{1}L_{2}} \ $の関係があるので変形すると，$ \ L_{1}L_{2}≧{M_{0}}^{2} \ $と求められる。

(2)解答：ワ
ワンポイント解説「4.二つのコイルに蓄えられるエネルギー$ \ W \ $」の通り，自己インダクタンスがそれぞれ$ \ L_{1} \ $，$ \ L_{2} \ $，相互インダクタンスが$ \ M_{0}\cos \theta \ $なので，磁気エネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}L_{1}{I_{1}}^{2}+\frac {1}{2}L_{2}{I_{2}}^{2}+M_{0}I_{1}I_{2}\cos \theta \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：チ
(2)解答式を$ \ \theta \ $で偏微分すると，
\[
\begin{eqnarray}
\frac{ \partial W }{ \partial \theta } &=&0+0-M_{0}I_{1}I_{2}\sin \theta \\[ 5pt ] &=&-M_{0}I_{1}I_{2}\sin \theta \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：イ
ワンポイント解説「1.ファラデーの電磁誘導の法則と自己インダクタンス$ \ L \ $」の通り，コイル$ \ 1 \ $の電流$ \ I_{1} \ $により鎖交する磁束は$ \ L_{1}I_{1} \ $であり，ワンポイント解説「2.相互インダクタンス$ \ M \ $」の通り，コイル$ \ 2 \ $の電流$ \ I_{2} \ $により鎖交する磁束は$ \ M_{0}I_{2}\cos \omega t \ $なので，コイル$ \ 1 \ $に鎖交する磁束$ \ \mathit {\Phi }_{1} \ $は，
\[
\begin{eqnarray}
\mathit {\Phi }_{1} &=&L_{1}I_{1}+M_{0}I_{2}\cos \omega t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヨ
ファラデーの電磁誘導の法則によりコイル$ \ 1 \ $に発生する起電力$ \ e \ $は，ワンポイント解説「1.ファラデーの電磁誘導の法則と自己インダクタンス$ \ L \ $」の通り，
\[
\begin{eqnarray}
e&=&−\frac {\mathrm {d} \mathit {\Phi }_{1}}{\mathrm {d} t} \\[ 5pt ] &=&−\frac {\mathrm {d} }{\mathrm {d} t}\left( L_{1}I_{1}+M_{0}I_{2}\cos \omega t \right) \\[ 5pt ] &=&−\left( 0-\omega M_{0}I_{2}\sin \omega t \right) \\[ 5pt ] &=&\omega M_{0}I_{2}\sin \omega t \\[ 5pt ] \end{eqnarray}
\] と求められる。