《電力》〈送電〉[H20:問16]三相3線式線路における電圧降下率に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

電線\( \ 1 \ \)線の抵抗が\( \ 5 \ \mathrm {[\Omega ]} \ \)，誘導性リアクタンスが\( \ 6 \ \mathrm {[\Omega ]} \ \)である三相\( \ 3 \ \)線式送電線について，次の(a)及び(b)に答えよ。

(a)　この送電線で受電端電圧を\( \ 60 \ \mathrm {[kV]} \ \)に保ちつつ，かつ，送電線での電圧降下率を受電端電圧基準で\( \ 10 \ \mathrm {[％]} \ \)に保つには，負荷の力率が\( \ 80 \ \mathrm {[％]} \ \) （遅れ）の場合に受電可能な三相皮相電力\( \ \mathrm {[MV\cdot A]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 27.4 \ \)　　(2)　\( \ 37.9 \ \)　　(3)　\( \ 47.4 \ \)　　(4)　\( \ 56.8 \ \)　　(5)　\( \ 60.5 \ \)

(b)　この送電線の受電端に，遅れ力率\( \ 60 \ \mathrm {[％]} \ \)で三相皮相電力\( \ 63.2 \ \mathrm {[MV\cdot A]} \ \)の負荷を接続しなければならなくなった。この場合でも受電端電圧を\( \ 60 \ \mathrm {[kV]} \ \)に，かつ，送電線での電圧降下率を受電端電圧基準で\( \ 10 \ \mathrm {[％]} \ \)に保ちたい。受電端に設置された調相設備から系統に供給すべき無効電力\( \ \mathrm {[Mvar]} \ \)の値として最も近いのは次のうちどれか。

　(1)　\( \ 12.6 \ \)　　(2)　\( \ 15.8 \ \)　　(3)　\( \ 18.3 \ \)　　(4)　\( \ 22.1 \ \)　　(5)　\( \ 34.8 \ \)

【ワンポイント解説】

三相\( \ 3 \ \)線式線路における電圧降下率を検討する問題です。
(b)については計算量が多い問題ですが，電圧降下の近似式を変形すれば比較的楽に解けるようになりますので，ぜひ本解答の内容を理解するようにして下さい。

1.三相\( \ 3 \ \)線式線路の電力
三相\( \ 3 \ \)線式の配電線の線間電圧が\( \ V \ \mathrm {[V]} \ \)，線電流が\( \ I \ \mathrm {[A]} \ \)，電圧と電流の力率が\( \ \cos \theta \ \)であるとき，皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)，有効電力\( \ P \ \mathrm {[W]} \ \)及び無効電力\( \ Q \ \mathrm {[var]} \ \)は，
\[
\begin{eqnarray}
S &=&\sqrt {3}VI \\[ 5pt ] P &=&\sqrt {3}VI\cos \theta \\[ 5pt ] Q &=&\sqrt {3}VI\sin \theta \\[ 5pt ] &=&\sqrt {3}VI\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] \end{eqnarray}
\] となります。

2.三相\( \ 3 \ \)線式送電線の電圧降下の近似式
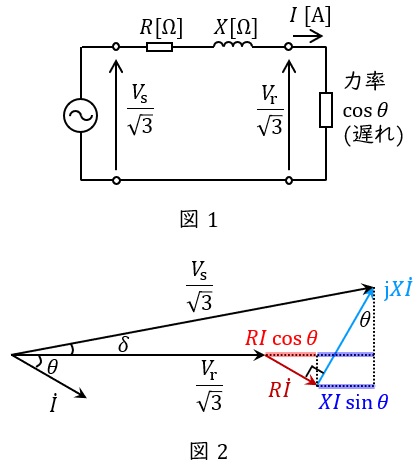
三相回路においては，一相分の等価回路及びベクトル図は図1及び図2のように描くことができ，送電端電圧と受電端電圧の位相差\( \ \delta \ \mathrm {[rad]} \ \)が無視できるぐらい小さいとしたときの電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&≃&\frac {V_{\mathrm {r}}}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ] \frac {V_{\mathrm {s}}}{\sqrt {3}}-\frac {V_{\mathrm {r}}}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ] V_{\mathrm {s}}-V_{\mathrm {r}}&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ] \varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] と求められ，電圧降下率\( \ ％\varepsilon \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％\varepsilon &=&\frac {\varepsilon }{V_{\mathrm {r}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) }{V_{\mathrm {r}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] となります。また，電圧降下の近似式を変形すると，
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] &=&R\cdot \sqrt {3}I \cos \theta +X \cdot \sqrt {3}I\sin \theta \\[ 5pt ] &=&\frac {R\cdot \sqrt {3}V_{\mathrm {r}}I \cos \theta +X \cdot \sqrt {3}V_{\mathrm {r}}I\sin \theta }{V_{\mathrm {r}}} \\[ 5pt ] &=&\frac {RP +XQ}{V_{\mathrm {r}}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(3)
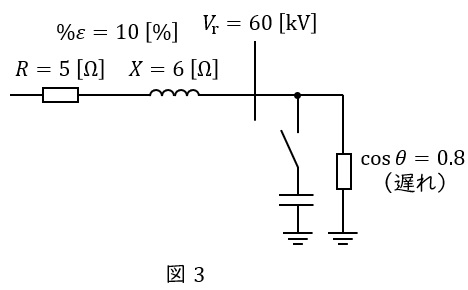
問題文に与えられている内容を単線図に示すと図3のようになる。
負荷の力率\( \ \cos \theta =0.8 \ \)なので，\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-0.8^{2}} \\[ 5pt ] &=&0.6 \\[ 5pt ] \end{eqnarray}
\] となり，送電線の電圧降下率\( \ ％\varepsilon =10 \ \mathrm {[％]} \ \)なので，電圧降下の大きさ\( \ \varepsilon \ \mathrm {[V]} \ \)は，ワンポイント解説「2.三相\( \ 3 \ \)線式送電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
％\varepsilon &=&\frac {\varepsilon }{V_{\mathrm {r}}}\times 100 \\[ 5pt ] \varepsilon &=&\frac {％\varepsilon V_{\mathrm {r}}}{100} \\[ 5pt ] &=&\frac {10 \times 60\times 10^{3}}{100} \\[ 5pt ] &=&6 \ 000 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] である。したがって，電圧降下の近似式より，送電線に流すことができる電流の最大値\( \ I \ \mathrm {[A]} \ \)は，ワンポイント解説「2.三相\( \ 3 \ \)線式送電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] I &=&\frac {\varepsilon }{\sqrt {3}\left( R\cos \theta +X\sin \theta \right) } \\[ 5pt ] &=&\frac {6 \ 000}{\sqrt {3}\times \left( 5\times 0.8 +6\times 0.6\right) } \\[ 5pt ] &≒&455.8 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，受電可能な三相皮相電力\( \ S \ \mathrm {[MV\cdot A]} \ \)は，ワンポイント解説「1.三相\( \ 3 \ \)線式線路の電力」の通り，
\[
\begin{eqnarray}
S &=&\sqrt {3}V_{\mathrm {r}}I \\[ 5pt ] &=&\sqrt {3}\times 60\times 10^{3}\times 455.8 \\[ 5pt ] &≒&47 \ 370 \ 000 \ \mathrm {[V\cdot A]}　→　47.4 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
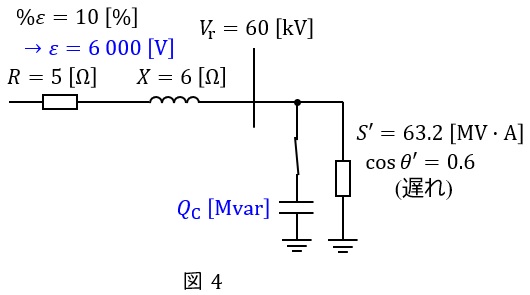
負荷変化後，調相設備を接続したときの単線図を図4に示す。
負荷の有効電力\( \ P \ \mathrm {[MW]} \ \)及び無効電力\( \ Q \ \mathrm {[Mvar]} \ \)は，ワンポイント解説「1.三相\( \ 3 \ \)線式線路の電力」の通り，
\[
\begin{eqnarray}
P &=&S\cos \theta \\[ 5pt ] &=&63.2\times 0.6 \\[ 5pt ] &=&37.92 \ \mathrm {[MW]} \\[ 5pt ] Q &=&S\sin \theta \\[ 5pt ] &=&63.2\times 0.8 \\[ 5pt ] &=&50.56 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] であるので，接続するコンデンサの容量を\( \ Q_{\mathrm {C}} \ \mathrm {[Mvar]} \ \)とすると，全体の電圧降下\( \ \varepsilon =6 \ 000 \ \mathrm {[V]} \ \)を保つことから，ワンポイント解説「2.三相\( \ 3 \ \)線式送電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
\varepsilon &=&\frac {RP +X\left( Q-Q_{\mathrm {C}}\right) }{V_{\mathrm {r}}} \\[ 5pt ] RP +X\left( Q-Q_{\mathrm {C}}\right) &=&\varepsilon V_{\mathrm {r}} \\[ 5pt ] X\left( Q-Q_{\mathrm {C}}\right) &=&\varepsilon V_{\mathrm {r}}-RP \\[ 5pt ] Q-Q_{\mathrm {C}} &=&\frac {\varepsilon V_{\mathrm {r}}-RP}{X} \\[ 5pt ] Q_{\mathrm {C}} &=&Q-\frac {\varepsilon V_{\mathrm {r}}-RP}{X} \\[ 5pt ] &=&50.56\times 10^{6}-\frac {6 \ 000 \times 60 \times 10^{3}-5\times 37.92\times 10^{6}}{6} \\[ 5pt ] &=&22.16\times 10^{6}\ \mathrm {[var]}　→　22.2 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。