《電力》〈送電〉[H29:問16]ケーブルの対地静電容量に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

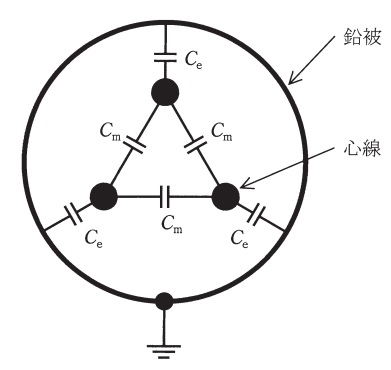
図に示すように，対地静電容量\( \ C_{\mathrm {e}} \ [\mathrm {F}] \ \)，線間静電容量\( \ C_{\mathrm {m}} \ [\mathrm {F}] \ \)からなる定格電圧\( \ E \ [\mathrm {V}] \ \)の三相1回線のケーブルがある。
今，受電端を開放した状態で，送電端で三つの心線を一括してこれと大地間に定格電圧\( \ E \ [\mathrm {V}] \ \)の\( \ \displaystyle \frac {1}{\sqrt {3}} \ \)倍の交流電圧を加えて充電すると全充電電流は\( \ 90 \ \mathrm {A} \ \)であった。
次に，二つの心線の受電端・送電端を接地し，受電端を開放した残りの心線と大地間に定格電圧\( \ E \ [\mathrm {V}] \ \)の\( \ \displaystyle \frac {1}{\sqrt {3}} \ \)倍の交流電圧を送電端に加えて充電するとこの心線に流れる充電電流は\( \ 45 \ \mathrm {A} \ \)であった。
次の(a)及び(b)に答えよ。
ただし，ケーブルの鉛被は接地されているとする。また，各心線の抵抗とインダクタンスは無視するものとする。なお，定格電圧及び交流電圧の周波数は，一定の商用周波数とする。

(a)　対地静電容量\( \ C_{\mathrm {e}} \ [\mathrm {F}] \ \)と線間静電容量\( \ C_{\mathrm {m}} \ [\mathrm {F}] \ \)の比\( \ \displaystyle \frac {C_{\mathrm {e}}}{C_{\mathrm {m}}} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(0.5\)　　(2)　\(1.0\)　　(3)　\(1.5\)　　(4)　\(2.0\)　　(5)　\(4.0\)

(b)　このケーブルの受電端をすべて開放して定格の三相電圧を送電端に加えたときに1線に流れる充電電流の値\( \ [\mathrm {A}] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(52.5\)　　(2)　\(75\)　　(3)　\(105\)　　(4)　\(120\)　　(5)　\(135\)

【ワンポイント解説】

本問のようなケーブルの静電容量の問題は，比較的難しめの問題が多いです。三種ではなく二種で出題されてもおかしくないレベルの問題です。試験までにケーブルの静電容量と充電電流を導出できるように準備しておきたいところです。

1.ケーブルの静電容量\( \ C \ \)
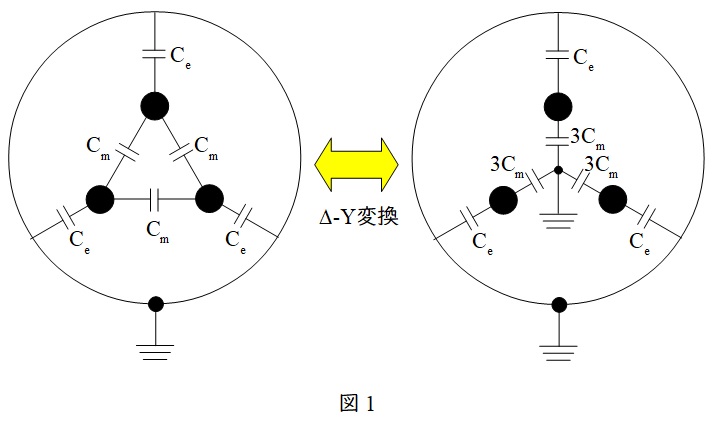
図1の通り対地静電容量\( \ C_{\mathrm {e}} \ [\mathrm {F}] \ \)，線間静電容量\( \ C_{\mathrm {m}} \ [\mathrm {F}] \ \)とすると，\( \ C_{\mathrm {m}} \ [\mathrm {F}] \ \)は\( \ \Delta -\mathrm {Y} \ \)変換により\( \ 3C_{\mathrm {m}} \ \)の\( \ \mathrm {Y} \ \)回路に変換できます。中性点の電位は\( \ 0 \ \)であるから，\( \ 3C_{\mathrm {m}} \ \)と\( \ C_{\mathrm {e}} \ \)は並列となるため，\( \ 1 \ \)相あたりの静電容量\( \ C \ \)は，
\[
\begin{eqnarray}
C&=&C_{\mathrm {e}}+3C_{\mathrm {m}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.ケーブルの充電電流\( \ I_{\mathrm {C}} \ \)
ケーブル\( \ 1 \ \)相あたりの静電容量\( \ C \ \)，線間電圧\( \ V \ \)とすると，ケーブルの充電電流\( \ I_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {C}}&=&\frac {\displaystyle \frac {V}{\sqrt {3}}}{\displaystyle \frac {1}{\omega C}} \\[ 5pt ] &=&\frac {\omega CV}{\sqrt {3}} \\[ 5pt ] &=&\frac {2\pi fCV}{\sqrt {3}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(5)
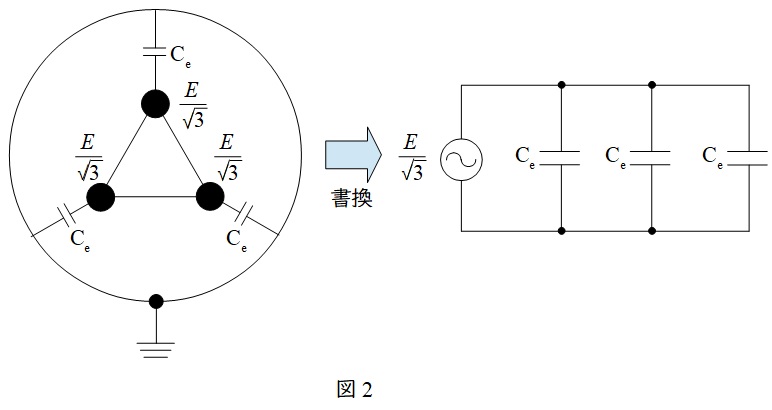
三つ心線を一括して交流電圧を加えた場合，回路は図2のように書き換えることができる。図2より合成静電容量が\( \ 3C_{\mathrm {e}} \ \)となるので，ケーブルの充電電流\( \ I_{\mathrm {C1}} \ \)は，角周波数\( \ \omega \ \)として，
\[
\begin{eqnarray}
I_{\mathrm {C1}}&=&\frac {3\omega C_{\mathrm {e}}E}{\sqrt {3}} &=&90 \ \mathrm {[A]}　　・・・・・・・　① \\[ 5pt ] \end{eqnarray}
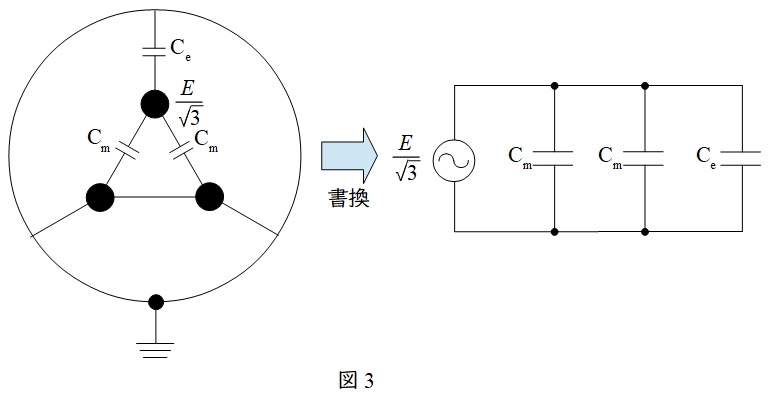
\] と求められる。一方，二つの心線の受電端・送電端を接地し，受電端を開放した残りの心線に交流電圧を加えた場合，回路は図3のように書き換えることができ，図3より合成静電容量が\( \ C_{\mathrm {e}}+2C_{\mathrm {m}} \ \)となるので，ケーブルの充電電流\( \ I_{\mathrm {C2}} \ \)は，角周波数\( \ \omega \ \)として，
\[
\begin{eqnarray}
I_{\mathrm {C2}}&=&\frac {\omega (C_{\mathrm {e}}+2C_{\mathrm {m}})E}{\sqrt {3}} &=&45 \ \mathrm {[A]}　　・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となる。①を\( \ C_{\mathrm {e}} \ \)について整理すると，
\[
\begin{eqnarray}
C_{\mathrm {e}}&=&\frac {90\sqrt {3}}{3\omega E} \\[ 5pt ] &=&\frac {30\sqrt {3}}{\omega E}　　・・・・・・・　①’ \\[ 5pt ] \end{eqnarray}
\] となるので，②を整理して①’を代入すると，
\[
\begin{eqnarray}
C_{\mathrm {e}}+2C_{\mathrm {m}}&=&\frac {45\sqrt {3}}{\omega E}\\[ 5pt ] \frac {30\sqrt {3}}{\omega E}+2C_{\mathrm {m}}&=&\frac {45\sqrt {3}}{\omega E}\\[ 5pt ] C_{\mathrm {m}}&=&\frac {15\sqrt {3}}{2\omega E}\\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ C_{\mathrm {e}} \ \)と\( \ C_{\mathrm {m}} \ \)の比は，
\[
\frac {C_{\mathrm {e}}}{C_{\mathrm {m}}}=\frac {\displaystyle \frac {30\sqrt {3}}{\omega E}}{\displaystyle \frac {15\sqrt {3}}{2\omega E}}=4.0
\] と求められる。

(b)解答：(1)
ワンポイント解説「1.ケーブルの静電容量\( \ C \ \)」と(a)の解答より，ケーブルの静電容量\( \ C \ \)は，
\[
\begin{eqnarray}
C&=&C_{\mathrm {e}}+3C_{\mathrm {m}}\\[ 5pt ] &=&4C_{\mathrm {m}}+3C_{\mathrm {m}}\\[ 5pt ] &=&7C_{\mathrm {m}}\\[ 5pt ] &=&\frac {105\sqrt {3}}{2\omega E}
\end{eqnarray}
\] であるから，充電電流\( \ I_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {C}}&=&\frac {\omega CE}{\sqrt {3}}\\[ 5pt ] &=&\frac {\omega E}{\sqrt {3}}\cdot \frac {105\sqrt {3}}{2\omega E}\\[ 5pt ] &=&\frac {105\sqrt {3}\omega E}{2\sqrt {3}\omega E}\\[ 5pt ] &=&52.5 [\mathrm {A}] \end{eqnarray}
\] と求められる。