《電力》〈変電〉[H22:問7]大容量発電所の主変圧器の結線方式とその理由に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

大容量発電所の主変圧器の結線を一次側三角形，二次側星形とするのは，二次側の線間電圧は相電圧の\( \ \fbox {　 （ア） 　} \ \)倍，線電流は相電流の\( \ \fbox {　 （イ） 　} \ \)倍であるため，変圧比を大きくすることができ，\( \ \fbox {　 （ウ） 　} \ \)に適するからである。また，一次側の結線が三角形であるから，\( \ \fbox {　 （エ） 　} \ \)電流は巻線内を環流するので二次側への影響がなくなるため，通信障害を抑制できる。

一次側を三角形，二次側を星形に接続した主変圧器の一次電圧と二次電圧の位相差は，\( \ \fbox {　 （オ） 　} \ \mathrm {[rad]} \ \)である。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる語句，式又は数値として，正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 　\sqrt {3}　 & 　1　 & 　昇　圧　 & 　第 \ 3 \ 調波　 & 　\displaystyle \frac {\pi }{6}　 \\
\hline
(2) & 　\displaystyle \frac {1}{\sqrt {3}}　 & 　\sqrt {3}　 & 　降　圧　 & 　零　相　 & 　0　 \\
\hline
(3) & 　\sqrt {3}　 & 　\displaystyle \frac {1}{\sqrt {3}}　 & 　昇　圧　 & 　高周波　 & 　\displaystyle \frac {\pi }{3}　 \\
\hline
(4) & 　\sqrt {3}　 & 　\displaystyle \frac {1}{\sqrt {3}}　 & 　降　圧　 & 　零　相　 & 　\displaystyle \frac {\pi }{3}　 \\
\hline
(5) & 　\displaystyle \frac {1}{\sqrt {3}}　 & 　1　 & 　昇　圧　 & 　第 \ 3 \ 調波　 & 　0　 \\
\hline
\end{array}
\]

【ワンポイント解説】

大容量発電所から送電するために使用される主変圧器に関する問題です。
\( \ \Delta \ \)接続と\( \ \mathrm {Y} \ \)接続の特徴とその違いは，電験でも出題頻度が高く，全科目で出題される可能性がある内容ですので，よく理解しておくようにしましょう。

1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
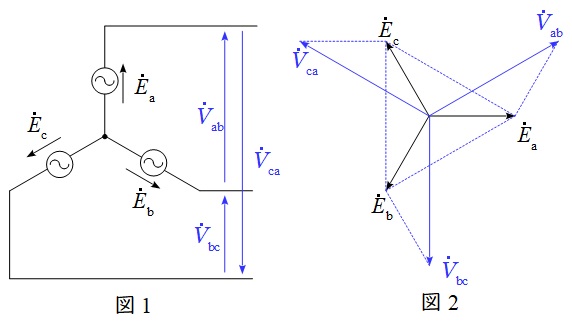
図1のような三相対称電源がある時，線間電圧と相電圧の関係は図2のベクトル図のようになり，線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると，
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ] V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ] V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)進みであることが分かります。

2.\( \ \Delta \ \)結線における相電流と線電流の関係
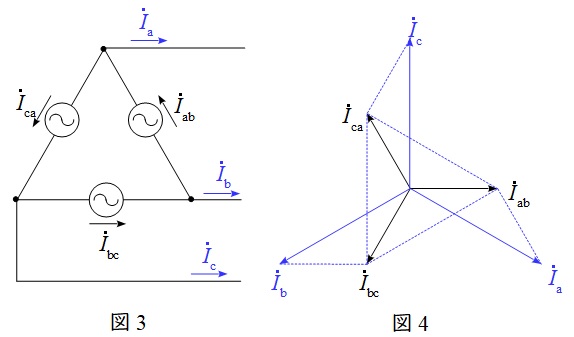
図3のような三相対称電源がある時，線電流と相電流の関係は図4のベクトル図のようになり，線電流の大きさは相電流の大きさと比較すると，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ] I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ] I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)遅れであることが分かります。

3.\( \ \Delta – \mathrm {Y} \ \)結線の電圧の角変位
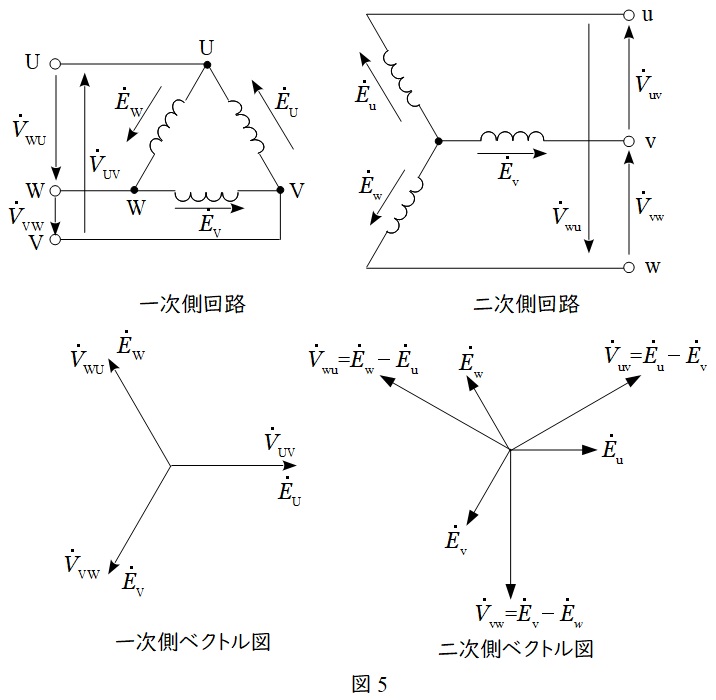
一次側\( \ \Delta \ \)，二次側\( \ \mathrm {Y} \ \)の回路図とベクトル図を描くと図5のようになります。各部の電圧は図の通りです。
一次側の相電圧\( \ E_{\mathrm {U}} \ \)，\( \ E_{\mathrm {V}} \ \)，\( \ E_{\mathrm {W}} \ \)と一次側の線間電圧\( \ V_{\mathrm {UV}} \ \)，\( \ V_{\mathrm {VW}} \ \)，\( \ V_{\mathrm {WU}} \ \)は全く同じ電圧であるので，一次側のベクトル図は図5左下のように描けます。
次に，一次側の相電圧\( \ E_{\mathrm {U}} \ \)，\( \ E_{\mathrm {V}} \ \)，\( \ E_{\mathrm {W}} \ \)と二次側の\( \ E_{\mathrm {u}} \ \)，\( \ E_{\mathrm {v}} \ \)，\( \ E_{\mathrm {w}} \ \)の位相は等しいので，二次側の\( \ E_{\mathrm {u}} \ \)，\( \ E_{\mathrm {v}} \ \)，\( \ E_{\mathrm {w}} \ \)のベクトルの向きは\( \ E_{\mathrm {U}} \ \)，\( \ E_{\mathrm {V}} \ \)，\( \ E_{\mathrm {W}} \ \)と同じになります。
また，回路図より二次側の線間電圧\( \ V_{\mathrm {uv}} \ \)，\( \ V_{\mathrm {vw}} \ \)，\( \ V_{\mathrm {wu}} \ \)は，
\[
{\dot V}_{\mathrm {uv}}={\dot E}_{\mathrm {u}}-{\dot E}_{\mathrm {v}}，{\dot V}_{\mathrm {vw}}={\dot E}_{\mathrm {v}}-{\dot E}_{\mathrm {w}}，{\dot V}_{\mathrm {wu}}={\dot E}_{\mathrm {w}}-{\dot E}_{\mathrm {u}}
\] となり，ベクトル図は図5右下のように描けます。
結果的に\( \ V_{\mathrm {uv}} \ \)は\( \ V_{\mathrm {UV}} \ \)より\( \ \displaystyle 30°\left( \frac {\pi }{6} \ \mathrm {[rad]}\right) \ \)進むことになります。

【解答】

解答：(1)
(ア)
ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り，\( \ \mathrm {Y} \ \)結線における線間電圧は相電圧の\( \ \sqrt {3} \ \)倍となります。

(イ)
ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り，\( \ \mathrm {Y} \ \)結線においては相電流と線電流は等しいので\( \ 1 \ \)倍となります。

(ウ)
二次側の線間電圧が相電圧の\( \ \sqrt {3} \ \)倍であることから，\( \ \Delta – \mathrm {Y} \ \)結線方式はより昇圧に適することがわかります。

(エ)
\( \ \Delta \ \)結線においては第\( \ 3 \ \)調波電流を還流することができるという特徴があります。

(オ)
ワンポイント解説「3.\( \ \Delta – \mathrm {Y} \ \)結線の電圧の角変位」の通り，一次電圧と二次電圧の位相差は\( \ \displaystyle 30°\left( \frac {\pi }{6} \ \mathrm {[rad]}\right) \ \)となります。