《電力》〈送電〉[H27:問15]速度調定率と出力の関係に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

定格出力\( \ \mathrm {1000 \ MW} \ \)，速度調定率\( \ \mathrm {5 \ ％} \ \)のタービン発電機と，定格出力\( \ \mathrm {300 \ MW} \ \)，速度調定率\( \ \mathrm {3 \ ％} \ \)の水車発電機が周波数調整用に電力系統に接続されており，タービン発電機は\( \ \mathrm {80 \ ％} \ \)出力，水車発電機は\( \ \mathrm {60 \ ％} \ \)出力をとって，定格周波数(\( \ \mathrm {60 \ Hz} \ \))にてガバナフリー運転を行っている。

系統の負荷が急変したため，タービン発電機と水車発電機は速度調定率に従って出力を変化させた。次の(a)及び(b)の問に答えよ。

ただし，このガバナフリー運転におけるガバナ特性は直線とし，次式で表される速度調定率に従うものとする。また，この系統内で周波数調整を行っている発電機はこの\( \ 2 \ \)台のみとする。

　　　速度調定率\(\displaystyle =\frac {\displaystyle \frac {n_{2}-n_{1}}{n_{\mathrm {n}}}}{\displaystyle \frac {P_{1}-P_{2}}{P_{\mathrm {n}}}}\times 100 \ [％]\)

\(P_{1}\)：初期出力\( \ \mathrm {[MW]} \ \)　　　　　\(n_{1}\)：出力\(P_{1}\)における回転速度\( \ \mathrm {[min ^{-1}]} \ \)
\(P_{2}\)：変化後の出力\( \ \mathrm {[MW]} \ \)　　　\(n_{2}\)：変化後の出力\(P_{2}\)における回転速度\( \ \mathrm {[min ^{-1}]} \ \)
\(P_{\mathrm {n}}\)：定格出力\( \ \mathrm {[MW]} \ \)　　　　　\(n_{\mathrm {n}}\)：定格回転速度\( \ \mathrm {[min ^{-1}]} \ \)

(a)　出力を変化させ，安定した後のタービン発電機の出力は\( \ \mathrm {900 \ MW} \ \)となった。このときの系統周波数の値\( \ \mathrm {[Hz]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 59.5 \ \)　　(2)　\( \ 59.7 \ \)　　(3)　\( \ 60 \ \)　　(4)　\( \ 60.3 \ \)　　(5)　\( \ 60.5 \ \)

(b)　出力を変化させ，安定した後の水車発電機の出力の値\( \ \mathrm {[MW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 130 \ \)　　(2)　\( \ 150 \ \)　　(3)　\( \ 180 \ \)　　(4)　\( \ 210 \ \)　　(5)　\( \ 230 \ \)

【ワンポイント解説】

速度調定率の問題は非常によく出題される問題の一つです。問題文を図に描くことにより整理して，解けるようにしましょう。また，本問では速度調定率の公式は与えられていますが，速度調定率の式は覚えておくようにして下さい。

【解答】

(a)解答：(2)
タービン発電機の初期出力\( \ P_{\mathrm {1a}} \ \)と水車発電機出力\( \ P_{\mathrm {1b}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {1a}}&=&1000\times 0.8&=&800 \ [\mathrm {MW}] \\[ 5pt ] P_{\mathrm {1b}}&=&300\times 0.6&=&180 \ [\mathrm {MW}] \\[ 5pt ] \end{eqnarray}
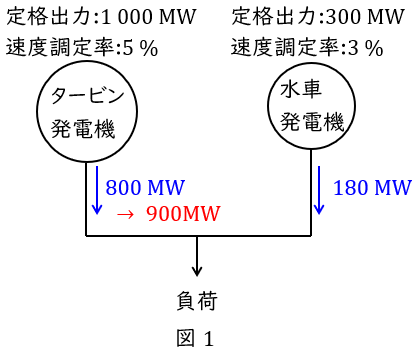
\] となる。よって，題意に沿って図を描くと図1のようになる。回転数\( \ n \ \)と周波数\( \ f \ \)との関係は，極数を\( \ p \ \)とすると\(\displaystyle \ n=\frac {120f}{p} \ \)の関係があるので，速度調定率\( \ \varepsilon \ \)の式は，
\[
\begin{eqnarray}
\varepsilon &=&\frac {\displaystyle \frac {n_{2}-n_{1}}{n_{\mathrm {n}}}}{\displaystyle \frac {P_{1}-P_{2}}{P_{\mathrm {n}}}}\times 100 [％] \\[ 5pt ] &=&\frac {\displaystyle \frac {f_{2}-f_{1}}{f_{\mathrm {n}}}}{\displaystyle \frac {P_{1}-P_{2}}{P_{\mathrm {n}}}}\times 100 \ [％] \end{eqnarray}
\] となる。したがって，上式に各値を代入すると，
\[
\begin{eqnarray}
\varepsilon &=&\frac {\displaystyle \frac {f_{2}-f_{1}}{f_{\mathrm {n}}}}{\displaystyle \frac {P_{1}-P_{2}}{P_{\mathrm {n}}}}\times 100 \\[ 5pt ] 5 &=&\frac {\displaystyle \frac {f_{2}-60}{60}}{\displaystyle \frac {800-900}{1000}}\times 100 \\[ 5pt ] f_{2} &=&59.7 \ \mathrm {[Hz]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(5)
速度調定率の式に各値を代入すると，
\[
\begin{eqnarray}
\varepsilon &=&\frac {\displaystyle \frac {f_{2}-f_{1}}{f_{\mathrm {n}}}}{\displaystyle \frac {P_{1}-P_{2}}{P_{\mathrm {n}}}}\times 100 \\[ 5pt ] 3 &=&\frac {\displaystyle \frac {59.7-60}{60}}{\displaystyle \frac {180-P_{2}}{300}}\times 100 \\[ 5pt ] P_{2} &=&230 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。