《電力》〈配電〉[H27:問16]三相3線式の回路計算に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

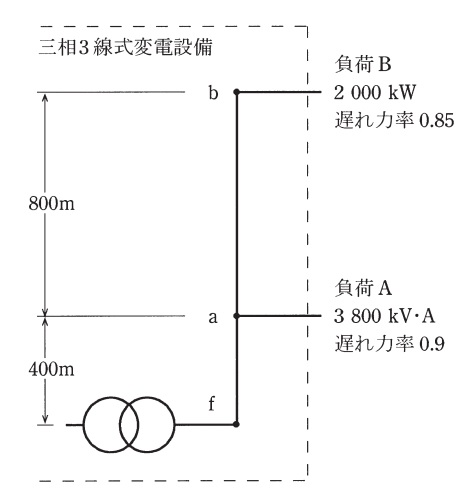
図は，三相\( \ 3 \ \)線式変電設備を単線図で表したものである。

現在，この変電設備は，\( \ \mathrm {a} \ \)点から\( \ \mathrm {3800 \ kV\cdot A} \ \)，遅れ力率\( \ \mathrm {0.9} \ \)の負荷\( \ \mathrm {A} \ \)と，\( \ \mathrm {b} \ \)点から\( \ \mathrm {2000 \ kW} \ \)，遅れ力率\( \ \mathrm {0.85} \ \)の負荷\( \ \mathrm {B} \ \)に電力を供給している。\( \ \mathrm {b} \ \)点の線間電圧の測定値が\( \ \mathrm {22000 \ V} \ \)であるとき，次の(a)及び(b)の問に答えよ。

なお，\( \ \mathrm {f} \ \)点と\( \ \mathrm {a} \ \)点の間は\( \ \mathrm {400 \ m} \ \)，\( \ \mathrm {a} \ \)点と\( \ \mathrm {b} \ \)点の間は\( \ \mathrm {800 \ m} \ \)で，電線1条当たりの抵抗とリアクタンスは\( \ \mathrm {1 \ km} \ \)当たり\( \ 0.24 \ \Omega \ \)と\( \ 0.18 \ \Omega \ \)とする。また，負荷は平衡三相負荷とする。

(a)　負荷\( \ \mathrm {A} \ \)と負荷\( \ \mathrm {B} \ \)で消費される無効電力の合計値\( \ \mathrm {[kvar]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 2710 \ \)　　(2)　\( \ 2900 \ \)　　(3)　\( \ 3080 \ \)　　(4)　\( \ 4880 \ \)　　(5)　\( \ 5120 \ \)

(b)　\( \ \mathrm {f-b} \ \)間の線間電圧の電圧降下\( \ V_{\mathrm {fb}} \ \)の値\( \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　　ただし，送電端電圧と受電端電圧との相差角が小さいとして得られる近似式を用いて解答すること。

　(1)　\( \ 23 \ \)　　(2)　\( \ 33 \ \)　　(3)　\( \ 59 \ \)　　(4)　\( \ 81 \ \)　　(5)　\( \ 101 \ \)

【ワンポイント解説】

(a)は標準的な内容ですが，(b)は三種としてはかなり難易度が高い問題です。線路の電圧降下の式を理解しておくことはもちろんですが，計算も電験三種の最高レベルの計算量です。

1.三相線路の電力\( \ P \ \)と電圧\( \ V \ \)，電流\( \ I \ \)の関係
電圧と電圧の位相差を\( \ \theta \ \)，力率を\( \ \cos \theta \ \)とすると，
\[
P=\sqrt {3}VI\cos \theta
\] となります。

2.送電線の電圧降下\( \ v \ \)
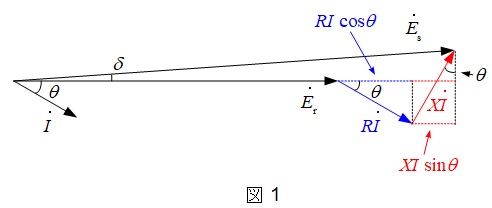
線路負荷が遅れ力率\( \ \cos \theta \ \)であるとき，電源側の電圧\( \ E_{\mathrm {s}} \ \)，受電側の電圧\( \ E_{\mathrm {r}} \ \)，線路電流を\( \ I \ \)とすると，ベクトル図は図1のように描けます。
図1より，操作角\( \ \delta \ \)が十分に小さいとすると，
\[
\begin{eqnarray}
E_{\mathrm {s}}&≒&E_{\mathrm {r}}+RI\cos\theta +XI\sin \theta \\[ 5pt ] E_{\mathrm {s}}-E_{\mathrm {r}}&=&I (R\cos\theta +X\sin \theta ) \\[ 5pt ] \end{eqnarray}
\] となります。三相3線式交流に関しては，線間電圧\( \ V_{\mathrm {s}} \ \)と\( \ V_{\mathrm {r}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {s}}&=&\sqrt {3} E_{\mathrm {s}} \\[ 5pt ] V_{\mathrm {r}}&=&\sqrt {3} E_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
E_{\mathrm {s}}-E_{\mathrm {r}}&=&I (R\cos\theta +X\sin \theta ) \\[ 5pt ] V_{\mathrm {s}}-V_{\mathrm {r}}&=&\sqrt {3}I (R\cos\theta +X\sin \theta ) \\[ 5pt ] v&=&\sqrt {3}I (R\cos\theta +X\sin \theta ) \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(2)
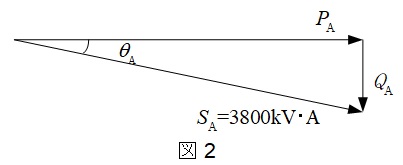
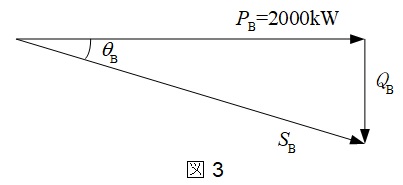
負荷\( \ \mathrm {A} \ \)，負荷\( \ \mathrm {B} \ \)の電力ベクトル図を描くと図2，図3の通りとなる。
負荷\( \ \mathrm {A} \ \)の力率\( \ \cos \theta _{\mathrm {A}}=0.9 \ \)，負荷\( \ \mathrm {B} \ \)の力率\( \ \cos \theta _{\mathrm {B}}=0.85 \ \)であるから，
\[
\begin{eqnarray}
\sin \theta _{\mathrm {A}}&=&\sqrt {1-\cos ^{2}\theta _{\mathrm {A}}} \\[ 5pt ] &=&\sqrt {1-0.9 ^{2}} \\[ 5pt ] &≒&0.4359 \\[ 5pt ] \sin \theta _{\mathrm {B}}&=&\sqrt {1-\cos ^{2}\theta _{\mathrm {B}}} \\[ 5pt ] &=&\sqrt {1-0.85 ^{2}} \\[ 5pt ] &≒&0.5268 \\[ 5pt ] \end{eqnarray}
\] となる。よって，負荷負荷\( \ \mathrm {A} \ \)，負荷\( \ \mathrm {B} \ \)の無効電力\( \ Q _{\mathrm {A}} \ \)，\( \ Q _{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
Q _{\mathrm {A}}&=&S _{\mathrm {A}} \sin \theta _{\mathrm {A}} \\[ 5pt ] &=&3800\times 0.4359 \\[ 5pt ] &≒&1656 \ \mathrm {[kvar]} \\[ 5pt ] Q _{\mathrm {B}}&=&P _{\mathrm {B}} \tan \theta _{\mathrm {B}} \\[ 5pt ] &=&P _{\mathrm {B}} \frac {\sin \theta _{\mathrm {B}}}{\cos \theta _{\mathrm {B}}} \\[ 5pt ] &=&2000 \times \frac {0.5268}{0.85} \\[ 5pt ] &≒&1240 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] となるので，無効電力の合計値は，
\[
\begin{eqnarray}
Q _{\mathrm {A}}+Q _{\mathrm {B}}&=&1656 + 1240 \\[ 5pt ] &=&2896　→　2900 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
\( \ \mathrm {a} \ \)点と\( \ \mathrm {b} \ \)点の間の線路抵抗\( \ R_{\mathrm {ab}} \ \)，線路リアクタンス\( \ X_{\mathrm {ab}} \ \)は，
\[
\begin{eqnarray}
R_{\mathrm {ab}}&=&0.24\times 0.8 \\[ 5pt ] &=&0.192 \ \mathrm {[\Omega ]}\\[ 5pt ] X_{\mathrm {ab}}&=&0.18\times 0.8 \\[ 5pt ] &=&0.144 \ \mathrm {[\Omega ]}\\[ 5pt ] \end{eqnarray}
\] となり，\( \ \mathrm {f} \ \)点と\( \ \mathrm {a} \ \)点の間の線路抵抗\( \ R_{\mathrm {fa}} \ \)，線路リアクタンス\( \ X_{\mathrm {fa}} \ \)は，
\[
\begin{eqnarray}
R_{\mathrm {fa}}&=&0.24\times 0.4 \\[ 5pt ] &=&0.096 \ \mathrm {[\Omega ]}\\[ 5pt ] X_{\mathrm {fa}}&=&0.18\times 0.4 \\[ 5pt ] &=&0.072 \ \mathrm {[\Omega ]}\\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.送電線の電圧降下\( \ v \ \)」より，電圧降下の近似式を変形すると，
\[
\begin{eqnarray}
v&=&\sqrt {3}I (R\cos\theta +X\sin \theta ) \\[ 5pt ] &=&\sqrt {3} \left( RI\cos\theta +XI\sin \theta \right) \\[ 5pt ] &=&\sqrt {3} \left( R\frac {P}{\sqrt {3}V} +X\frac {Q}{\sqrt {3}V} \right) \\[ 5pt ] &=&\frac {RP+XQ}{V} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ \mathrm {a} \ \)点と\( \ \mathrm {b} \ \)点の間の電圧降下\( \ v_{\mathrm {ab}} \ \)は，
\[
\begin{eqnarray}
v_{\mathrm {ab}}&=&\frac {R_{\mathrm {ab}}P_{\mathrm {B}}+X_{\mathrm {ab}}Q_{\mathrm {B}}}{V_{\mathrm {B}}} \\[ 5pt ] &=&\frac {0.192\times 2000\times 10^{3}+0.144\times 1240\times 10^{3}}{22000} \\[ 5pt ] &≒&25.57 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ \mathrm {a} \ \)点の線間電圧\( \ V _{\mathrm {A}} \ \)は，
\[
\begin{eqnarray}
V _{\mathrm {A}}&=&V _{\mathrm {B}}+ v_{\mathrm {ab}} \\[ 5pt ] &=&22000+25.57 \\[ 5pt ] &≒&22030 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。次に，\( \ \mathrm {f} \ \)点と\( \ \mathrm {a} \ \)点の間の電圧降下\( \ v_{\mathrm {fa}} \ \)は，
\[
\begin{eqnarray}
v_{\mathrm {fa}}&=&\frac {R_{\mathrm {fa}}\left( P_{\mathrm {A}}+P_{\mathrm {B}}\right) +X_{\mathrm {fa}}\left( Q_{\mathrm {A}}+Q_{\mathrm {B}}\right) }{V_{\mathrm {A}}} \\[ 5pt ] &=&\frac {0.096\times \left( 3800\times 10^{3}\times 0.9+2000\times 10^{3}\right) +0.072\times \left( 2896\times 10^{3}\right) }{22030} \\[ 5pt ] &≒&33.08 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ \mathrm {f-b} \ \)間の線間電圧の電圧降下\( \ V_{\mathrm {fb}} \ \)は，
\[
\begin{eqnarray}
v_{\mathrm {fb}}&=&v_{\mathrm {fa}}+v_{\mathrm {ab}} \\[ 5pt ] &=&25.57 +33.08 \\[ 5pt ] &≒&58.7 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。