《電力》〈水力〉[R4上:問15]揚水発電所の揚水運転時の必要電力量及び流量に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

揚水発電所について，次の(a)及び(b)の問に答えよ。

ただし，水の密度を\( \ 1 \ 000 \ \mathrm {kg / m^{3}} \ \)，重力加速度を\( \ 9.8 \ \mathrm {m / s^{2}} \ \)とする。

(a)　揚程\( \ 450 \ \mathrm {m} \ \)，ポンプ効率\( \ 90 \ \mathrm {％} \ \)，電動機効率\( \ 98 \ \mathrm {％} \ \)の揚水発電所がある。揚水により揚程及び効率は変わらないものとして，下池から\( \ 1 \ 800 \ 000 \ \mathrm {m^{3}} \ \)の水を揚水するのに電動機が要する電力量の値\( \ \mathrm {[MW\cdot h]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1 \ 500 \ \)　　(2)　\( \ 1 \ 750 \ \)　　(3)　\( \ 2 \ 000 \ \)　　(4)　\( \ 2 \ 250 \ \)　　(5)　\( \ 2 \ 500 \ \)

(b)　この揚水発電所において，発電電動機が電動機入力\( \ 300 \ \mathrm {MW} \ \)で揚水運転しているときの流量の値\( \ \mathrm {[m^{3} / s]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 50.0 \ \)　　(2)　\( \ 55.0 \ \)　　(3)　\( \ 60.0 \ \)　　(4)　\( \ 65.0 \ \)　　(5)　\( \ 70.0 \ \)

【ワンポイント解説】

揚水発電所の揚水運転時の必要動力や流量に関する問題です。
Ｂ問題の計算問題としては比較的取り組みやすい内容となりますので，完答を目指したい問題となります。

1.揚水発電所の諸公式
揚水発電で使用される諸公式は以下の通りです。本問で使用しない公式も覚えておくようにしましょう。

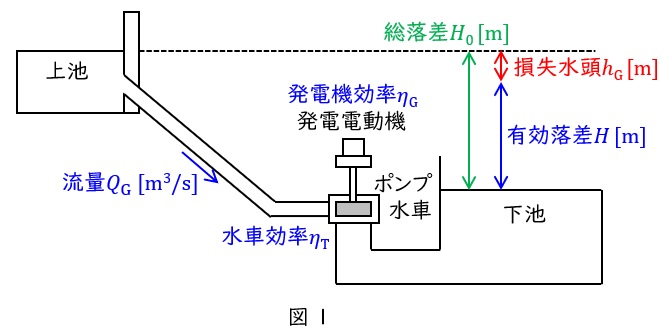
①発電電力
有効落差　：\( \ H=H_{0}-h_{\mathrm {G}} \ \mathrm {[ m ] } \ \)
発電機出力：\( \ P_{\mathrm {G}}=9.8Q_{\mathrm {G}}H\eta _{\mathrm {T}}\eta _{\mathrm {G}} \ \mathrm {[ kW ] } \ \)
総発電量　：\( \ W_{\mathrm {G}}=P_{\mathrm {G}}T_{\mathrm {G}} \ \mathrm {[ kW\cdot h ] } \ \)

ただし，\( \ H_{0} \ \)は総落差\( \ \mathrm {[m]} \ \)，\( \ h_{\mathrm {G}} \ \)は発電時の損失水頭\( \ \mathrm {[m]} \ \)，\( \ Q_{\mathrm {G}} \ \)は発電時の流量\( \ \mathrm {[m^{3} / s]} \ \)，\( \ \eta _{\mathrm {T}} \ \)は水車効率，\( \ \eta _{\mathrm {G}} \ \)は発電機効率，\( \ T_{\mathrm {G}} \ \)は発電時間\( \ \mathrm {[h]} \ \)

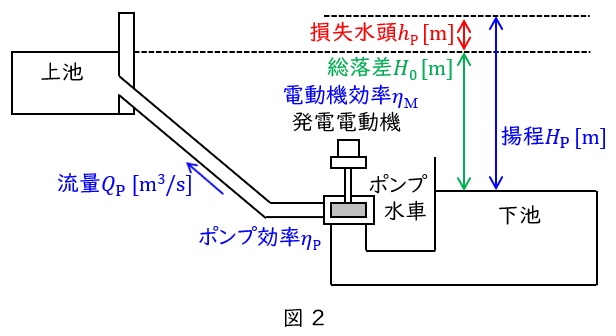
②揚水動力
必要揚程　：\( \ \displaystyle H_{\mathrm {P}}=H_{0}+h_{\mathrm {P}} \ \mathrm {[ m ] } \ \)
所要動力　：\( \ \displaystyle P_{\mathrm {M}}=\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} } \ \mathrm {[ kW ] } \ \)
所要電力量：\( \ W_{\mathrm {M}}=P_{\mathrm {M}}T_{\mathrm {M}} \ \mathrm {[ kW\cdot h ] } \ \)

ただし，\( \ H_{0} \ \)は総落差\( \ \mathrm {[m]} \ \)，\( \ h_{\mathrm {P}} \ \)は揚水時の損失水頭\( \ \mathrm {[m]} \ \)，\( \ Q_{\mathrm {P}} \ \)は揚水時の流量\( \ \mathrm {[m^{3} / s]} \ \)，\( \ \eta _{\mathrm {P}} \ \)はポンプ効率，\( \ \eta _{\mathrm {M}} \ \)は電動機効率，\( \ T_{\mathrm {M}} \ \)は揚水時間\( \ \mathrm {[h]} \ \)

③揚水総合効率
\[
\begin{eqnarray}
\eta &=&\frac {W_{\mathrm {G}}}{W_{\mathrm {M}}}\times 100\mathrm {[ ％ ] } \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(5)
揚程\( \ H_{\mathrm {P}}=450 \ \mathrm {[ m ] } \ \)，ポンプ効率\( \ \eta _{\mathrm {P}}=0.90 \ \)，電動機効率\( \ \eta _{\mathrm {M}}=0.98 \ \)であるから，揚水時の流量を\( \ Q_{\mathrm {P}} \ \ \mathrm {[m^{3} / s]} \ \)とすると，揚水に必要な動力\( \ P_{\mathrm {M}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.揚水発電所の諸公式」の通り，
\[
\begin{eqnarray}
P_{\mathrm {M}}&=&\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} } \\[ 5pt ] &=&\frac { 9.8Q_{\mathrm {P}}\times 450}{0.90\times 0.98} \\[ 5pt ] &=&5 \ 000Q_{\mathrm {P}} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，所要電力量\( \ W_{\mathrm {M}} \ \mathrm {[ kW\cdot h ] } \ \)は揚水時間を\( \ T_{\mathrm {M}} \ \mathrm {[h]} \ \)とすると，
\[
\begin{eqnarray}
W_{\mathrm {M}}&=&P_{\mathrm {M}}T_{\mathrm {M}} \\[ 5pt ] &=&5 \ 000Q_{\mathrm {P}}T_{\mathrm {M}}　　・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。ここで，揚水量\( \ V \ \mathrm {[m^{3}] } \ \)は，
\[
\begin{eqnarray}
V=Q_{\mathrm {P}}\times 3600\times T_{\mathrm {M}}&=&1 \ 800 \ 000 \\[ 5pt ] \end{eqnarray}
\] であることから，
\[
\begin{eqnarray}
Q_{\mathrm {P}}T_{\mathrm {M}}&=&500 \\[ 5pt ] \end{eqnarray}
\] となり，これを①式に代入すると，
\[
\begin{eqnarray}
W_{\mathrm {M}}&=&5 \ 000Q_{\mathrm {P}}T_{\mathrm {M}} \\[ 5pt ] &=&5 \ 000\times 500 \\[ 5pt ] &=&2 \ 500 \ 000 \ \mathrm {[ kW\cdot h ] }　→　2 \ 500 \ \mathrm {[MW\cdot h ] } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
(a)の条件及びワンポイント解説「1.揚水発電所の諸公式」より，揚水運転時の流量\( \ Q_{\mathrm {P}} \ \mathrm {[m^{3} / s]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {M}}&=&\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} } \\[ 5pt ] Q_{\mathrm {P}}&=&\frac {\eta _{\mathrm {P}}\eta _{\mathrm {M}} }{ 9.8H_{\mathrm {P}}}P_{\mathrm {M}} \\[ 5pt ] &=&\frac {0.90\times 0.98}{ 9.8\times 450}\times 300\times 10^{3} \\[ 5pt ] &=&60.0 \ \mathrm {[m^{3} / s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。