Contents
【問題】
【難易度】★★★☆☆(普通)
定格容量\( \ 80 \ \mathrm {MV\cdot A} \ \),一次側定格電圧\( \ 33 \ \mathrm {kV} \ \),二次側定格電圧\( \ 11 \ \mathrm {kV} \ \),百分率インピーダンス\( \ 18.3 \ \mathrm {%} \ \)(定格容量ベース)の三相変圧器\( \ \mathrm {T_{A}} \ \)がある。三相変圧器\( \ \mathrm {T_{A}} \ \)の一次側は\( \ 33 \ \mathrm {kV} \ \)の電源に接続され,二次側は負荷のみが接続されている。電源の百分率内部インピーダンスは,\( \ 1.5 \ \mathrm {%} \ \)(系統基準容量ベース)とする。ただし,系統基準容量は\( \ 80 \ \mathrm {MV\cdot A} \ \)である。なお,抵抗分及びその他の定数は無視する。次の(a)及び(b)の問に答えよ。
(a) 将来の負荷変動等は考えないものとすると,変圧器\( \ \mathrm {T_{A}} \ \)の二次側に設置する遮断器の定格遮断電流の値\( \ \mathrm {[kA]} \ \)として,最も適切なものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 5 \ \) (2) \( \ 8 \ \) (3) \( \ 12.5 \ \) (4) \( \ 20 \ \) (5) \( \ 25 \ \)
(b) 定格容量\( \ 50 \ \mathrm {MV\cdot A} \ \),百分率インピーダンスが\( \ 12.0 \ \mathrm {%} \ \)(定格容量ベース)の三相変圧器\( \ \mathrm {T_{B}} \ \)を三相変圧器\( \ \mathrm {T_{A}} \ \)と並列に接続した。\( \ 40 \ \mathrm {MW} \ \)の負荷をかけて運転した場合,三相変圧器\( \ \mathrm {T_{A}} \ \)の負荷分担の値\( \ \mathrm {[MW]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,三相変圧器群\( \ \mathrm {T_{A}} \ \)と\( \ \mathrm {T_{B}} \ \)にはこの負荷のみが接続されているものとし,抵抗分及びその他の定数は無視する。
(1) \( \ 15.8 \ \) (2) \( \ 19.5 \ \) (3) \( \ 20.5 \ \) (4) \( \ 24.2 \ \) (5) \( \ 24.6 \ \)
【ワンポイント解説】
百分率インピーダンスを用いた事故電流の計算と負荷分担の計算に関する問題です。
過去何度も同問題や類題が出題されている非常に重要な内容です。遮断器の定格遮断電流が計算結果よりも大きくしなければならないこと,\( \ \mathrm {T_{A}} \ \)と\( \ \mathrm {T_{B}} \ \)を間違えてしまう等躓くポイントは似ていますので,確実に理解するようにして下さい。
本問は令和4年上期問16及び平成22年問16からの再出題となります。
1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \),基準電流を\( \ I_{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.百分率インピーダンスの容量換算
「1.オーム法からパーセントインピーダンス法への変換」の通り,百分率インピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の百分率インピーダンスは,
\[
\begin{eqnarray}
%Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}%Z_{\mathrm {A}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.変圧器の負荷分担
並行運転の条件を満たす同じ基準容量の元での百分率インピーダンス\( \ %Z_{\mathrm {A}} \ \mathrm {[%]} \ \)の変圧器\( \ \mathrm {A} \ \)と百分率インピーダンス\( \ %Z_{\mathrm {B}} \ \mathrm {[%]} \ \)の変圧器\( \ \mathrm {B} \ \)があり,負荷\( \ P \ \mathrm {[W]} \ \)を接続するとき,それぞれの負荷分担\( \ P_{\mathrm {A}} \ \mathrm {[W]} \ \)及び\( \ P_{\mathrm {B}} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&\frac {%Z_{\mathrm {B}}}{%Z_{\mathrm {A}}+%Z_{\mathrm {B}}}P \\[ 5pt ]
P_{\mathrm {B}}&=&\frac {%Z_{\mathrm {A}}}{%Z_{\mathrm {A}}+%Z_{\mathrm {B}}}P \\[ 5pt ]
\end{eqnarray}
\]
と求められます。両変圧器とも一次二次電圧が等しいことから,分流の法則が適用できるという解釈で考えると良いかと思います。
4.百分率インピーダンスの短絡電流計算
百分率インピーダンスを\( \ %Z \ \)とすると,三相短絡電流\( \ I_{\mathrm {s}} \ \)は,基準電流\( \ I_{\mathrm {n}} \ \)を用いて,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{%Z/100} \\[ 5pt ]
&=&\frac {100I_{\mathrm {n}}}{%Z} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが,試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100I_{\mathrm {n}} \\[ 5pt ]
&=&\frac {100I_{\mathrm {n}}}{%Z_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(a)解答:(5)
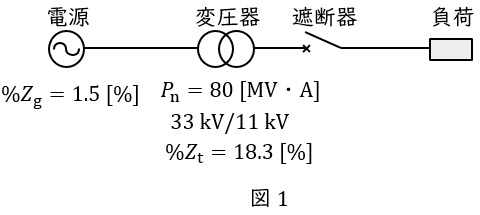
題意に沿って図を描くと図1のようになる。
図1において,負荷から電源側を見た百分率インピーダンス\( \ %Z \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z&=&%Z_{\mathrm {g}}+%Z_{\mathrm {t}} \\[ 5pt ]
&=&1.5+18.3 \\[ 5pt ]
&=&19.8 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
であり,変圧器二次側の基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {80\times 10^{6}}{\sqrt {3}\times 11\times 10^{3}} \\[ 5pt ]
&≒&4 \ 199 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,三相短絡発生時の事故電流\( \ I_{\mathrm {s}} \ \mathrm {[kA]} \ \)は,ワンポイント解説「4.百分率インピーダンスの短絡電流計算」の通り,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {100I_{\mathrm {n}}}{%Z} \\[ 5pt ]
&=&\frac {100\times 4 \ 199}{19.8} \\[ 5pt ]
&≒&21 \ 200 \ \mathrm {[A]} → 21.2 \ \mathrm {[kA]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,遮断器の定格遮断電流として最も適当なのは三相短絡電流より大きい\( \ 25 \ \mathrm {kA} \ \)と求められる。
(b)解答:(3)
三相変圧器\( \ \mathrm {T_{B}} \ \)の百分率インピーダンス\( \ %Z_{\mathrm {B}}=12.0 \ \mathrm {[%]} \ \)を\( \ 80 \ \mathrm {MV\cdot A} \ \)換算すると,ワンポイント解説「2.百分率インピーダンスの容量換算」より,
\[
\begin{eqnarray}
%Z_{\mathrm {B}}^{\prime }&=&\frac {80}{50}\times 12.0 \\[ 5pt ]
&=&19.2 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,三相変圧器\( \ \mathrm {T_{A}} \ \)の負荷分担の値\( \ P_{\mathrm {A}} \ \mathrm {[MW]} \ \)は,ワンポイント解説「3.変圧器の負荷分担」より,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&\frac {%Z_{\mathrm {B}}^{\prime }}{%Z_{\mathrm {A}}+%Z_{\mathrm {B}}^{\prime }}\times 40 \\[ 5pt ]
&=&\frac {19.2}{18.3+19.2}\times 40 \\[ 5pt ]
&≒&20.5 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは