《法規》〈電気施設管理〉[H23:問12]日負荷曲線からの不等率及び力率の導出に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

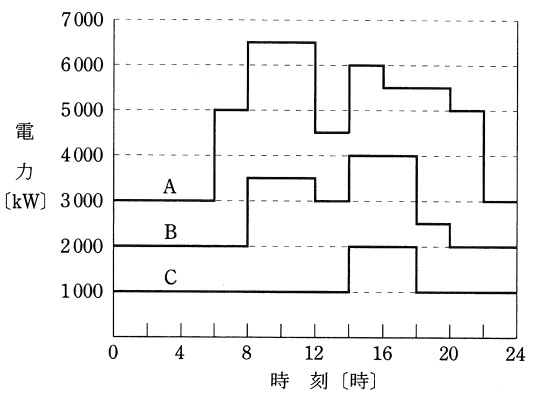
ある変電所において，図のような日負荷特性を有する三つの負荷群\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)に電力を供給している。この変電所に関して，次の(a)及び(b)の問に答えよ。
ただし，負荷群\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)の最大電力は，それぞれ\( \ 6 \ 500 \ \mathrm {[kW]} \ \)，\( \ 4 \ 000 \ \mathrm {[kW]} \ \)及び\( \ 2 \ 000 \ \mathrm {[kW]} \ \)とし，また，負荷群\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)の力率は時間に関係なく一定で，それぞれ\( \ 100 \ \mathrm {[％]} \ \)，\( \ 80 \ \mathrm {[％]} \ \)及び\( \ 60 \ \mathrm {[％]} \ \)とする。

(a)　不等率の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.98 \ \)　　(2)　\( \ 1.00 \ \)　　(3)　\( \ 1.02 \ \)　　(4)　\( \ 1.04 \ \)　　(5)　\( \ 1.06 \ \)

(b)　最大負荷時における総合力率\( \ \mathrm {[％]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 86.9 \ \)　　(2)　\( \ 87.7 \ \)　　(3)　\( \ 90.4 \ \)　　(4)　\( \ 91.1 \ \)　　(5)　\( \ 94.1 \ \)

【ワンポイント解説】

日負荷曲線に関する問題です。
日負荷曲線の計算問題は電気施設管理の中でも非常に出題されやすい問題となります。
需要率，不等率，負荷率はすべて定義として覚えておく必要がありますので，試験本番までに必ずマスターしておきましょう。

1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
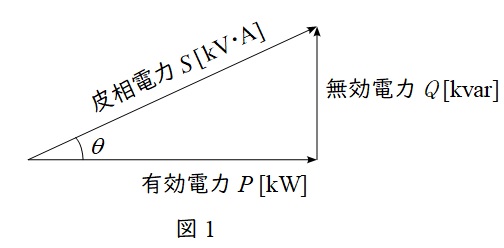
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

2.需要率，不等率，負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②不等率（常に\( \ 1 \ \)以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ] \end{eqnarray}
\]

③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(4)
負荷群\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)を合計した需要電力は下表の通りとなる。
\[
\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline
& 0\sim 6 & 6\sim 8 & 8\sim 12 & 12\sim 14 & 14\sim 16 & 16\sim 18 & 18\sim 20 & 20\sim 22 & 22\sim 24 \\
\hline
\mathrm {A} & 3 \ 000 & 5 \ 000 & 6 \ 500 & 4 \ 500 & 6 \ 000 & 5 \ 500 & 5 \ 500 & 5 \ 000 & 3 \ 000 \\
\hline
\mathrm {B} & 2 \ 000 & 2 \ 000 & 3 \ 500 & 3 \ 000 & 4 \ 000 & 4 \ 000 & 2 \ 500 & 2 \ 000 & 2 \ 000 \\
\hline
\mathrm {C} & 1 \ 000 & 1 \ 000 & 1 \ 000 & 1 \ 000 & 2 \ 000 & 2 \ 000 & 1 \ 000 & 1 \ 000 & 1 \ 000 \\
\hline
計 & 6 \ 000 & 8 \ 000 & 11 \ 000 & 8 \ 500 & 12 \ 000 & 11 \ 500 & 9 \ 000 & 8 \ 000 & 6 \ 000 \\
\hline
\end{array}
\] これより，合成最大需要電力は\( \ 14\sim 16 \ \)時の\( \ 12 \ 000 \ \mathrm {[kW]} \ \)であることがわかる。
よって，ワンポイント解説「2.需要率，不等率，負荷率の定義」より，不等率は，
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ] &=&\frac {6 \ 500+4 \ 000+2 \ 000}{12 \ 000} \\[ 5pt ] &≒&1.04 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
\( \ 14\sim 16 \ \)時の負荷群\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)の需要電力を\( \ P_{\mathrm {A}}=6 \ 000 \ \mathrm {[kW]} \ \)，\( \ P_{\mathrm {B}}=4 \ 000 \ \mathrm {[kW]} \ \)及び\( \ P_{\mathrm {C}}=2 \ 000 \ \mathrm {[kW]} \ \)とする。
題意より，それぞれの力率\( \ \cos \theta _{\mathrm {A}}=1 \ \)，\( \ \cos \theta _{\mathrm {B}}=0.8 \ \)及び\( \ \cos \theta _{\mathrm {C}}=0.6 \ \)であるから，それぞれの電力のベクトル図を描くと図2のようになる。
図2において，無効電力\( \ Q_{\mathrm {B}} \ \mathrm {[kvar]} \ \)及び\( \ Q_{\mathrm {C}} \ \mathrm {[kvar]} \ \)はそれぞれ，
\[
\begin{eqnarray}
Q_{\mathrm {B}}&=&S_{\mathrm {B}}\sin \theta _{\mathrm {B}} \\[ 5pt ] &=&\frac {P_{\mathrm {B}}}{\cos \theta _{\mathrm {B}}}\sqrt {1-\cos ^{2}\theta _{\mathrm {B}}} \\[ 5pt ] &=&\frac {4 \ 000}{0.8}\sqrt {1-0.8 ^{2}} \\[ 5pt ] &=&5 \ 000\times 0.6 \\[ 5pt ] &=&3 \ 000 \ \mathrm {[kvar]} \\[ 5pt ] Q_{\mathrm {C}}&=&S_{\mathrm {C}}\sin \theta _{\mathrm {C}} \\[ 5pt ] &=&\frac {P_{\mathrm {C}}}{\cos \theta _{\mathrm {C}}}\sqrt {1-\cos ^{2}\theta _{\mathrm {C}}} \\[ 5pt ] &=&\frac {2 \ 000}{0.6}\sqrt {1-0.6 ^{2}} \\[ 5pt ] &≒&3 \ 333\times 0.8 \\[ 5pt ] &≒&2 \ 666 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] となる。以上より，総合力率\( \ \cos \theta \ \)は，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P_{\mathrm {A}}+P_{\mathrm {B}}+P_{\mathrm {C}}}{S} \\[ 5pt ] &=&\frac {P_{\mathrm {A}}+P_{\mathrm {B}}+P_{\mathrm {C}}}{\sqrt {\left( P_{\mathrm {A}}+P_{\mathrm {B}}+P_{\mathrm {C}}\right) ^{2}+\left( Q_{\mathrm {B}}+Q_{\mathrm {C}}\right) ^{2}}} \\[ 5pt ] &=&\frac {6 \ 000+4 \ 000+2 \ 000}{\sqrt {\left( 6 \ 000+4 \ 000+2 \ 000\right) ^{2}+\left( 3 \ 000+2 \ 666\right) ^{2}}} \\[ 5pt ] &≒&\frac {12 \ 000}{13 \ 270} \\[ 5pt ] &≒&0.904　→　90.4 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。