《法規》〈電気施設管理〉[H25:問11]高圧進相コンデンサの劣化診断に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

高圧進相コンデンサの劣化診断について，次の(a)及び(b)の問に答えよ。

(a)　三相3線式\( \ 50 \ \mathrm {[Hz]} \ \)，使用電圧\( \ 6.6 \ \mathrm {[kV]} \ \)の高圧電路に接続された定格電圧\( \ 6.6 \ \mathrm {[kV]} \ \)，定格容量\( \ 50 \ \mathrm {[kvar]} \ \)（\( \ \mathrm {Y} \ \)結線，一相\( \ 2 \ \)素子)の高圧進相コンデンサがある。その内部素子の劣化度合い点検のため，運転電流を高圧クランプメータで定期的に測定していた。

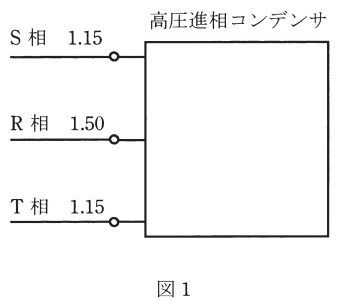
ある日の測定において，測定電流\( \ \mathrm {[A]} \ \)の定格電流\( \ \mathrm {[A]} \ \)に対する比は，図1のとおりであった。測定電流\( \ \mathrm {[A]} \ \)に最も近い数値の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，直列リアクトルはないものとして計算せよ。

\[
\begin{array}{cccc}
& 　\mathrm {R} \ 相　 & 　\mathrm {S} \ 相　 & 　\mathrm {T} \ 相　 \\
\hline
(1) & 6.6 & 5.0 & 5.0 \\
\hline
(2) & 7.5 & 5.7 & 5.7 \\
\hline
(3) & 3.8 & 2.9 & 2.9 \\
\hline
(4) & 11.3 & 8.6 & 8.6 \\
\hline
(5) & 7.2 & 5.5 & 5.5 \\
\hline
\end{array}
\]

(b)　(a)の測定により，劣化による内部素子の破壊(短絡)が発生していると判断し，機器停止のうえ各相間の静電容量を\( \ 2 \ \)端子測定法(\( \ 1 \ \)端子開放で測定)で測定した。

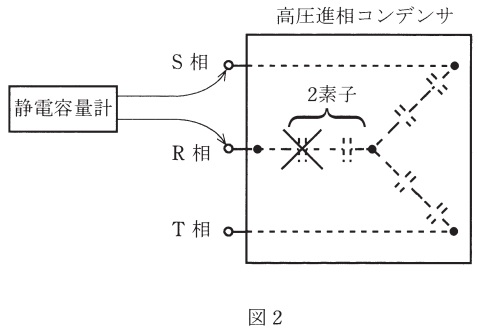
図2のとおりの内部結線における素子破壊(素子極間短絡)が発生しているとすれば，静電容量測定結果の記述として，正しいものを次の(1)～(5)のうちから一つ選べ。ただし，図中\( \times \)印は，破壊素子を表す。

(1)　\( \ \mathrm {R－S} \ \)相間の測定値は，最も小さい。

(2)　\( \ \mathrm {S－T} \ \)相間の測定値は，最も小さい。

(3)　\( \ \mathrm {T－R} \ \)相間は，測定不能である。

(4)　\( \ \mathrm {R－S} \ \)相間の測定値は，\( \ \mathrm {S－T} \ \)相間の測定値の約\( \ 75 \ \mathrm {[％]} \ \)である。

(5)　\( \ \mathrm {R－S} \ \)相間と\( \ \mathrm {S－T} \ \)相間の測定値は，等しい

【ワンポイント解説】

電力の送電に関する内容と，理論のコンデンサに関する内容を合わせたような応用問題と言えると思います。どちらの分野の中身もきちんと理解していればそれほど難解な計算はありません。

1.コンデンサの並列接続時及び直列接続時の静電容量
静電容量\( \ C_{1} \ \)及び\( \ C_{2} \ \)のコンデンサがある時，合成静電容量\( \ C \ \)は以下の通りとなります。

①並列
\[
\begin{eqnarray}
C &=& C_{1}+C_{2} \\[ 5pt ] \end{eqnarray}
\]

②直列
\[
\begin{eqnarray}
&&\frac {1}{C} &=& \frac {1}{C_{1}}+\frac {1}{C_{2}} \\[ 5pt ] &⇔&C &=& \frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(1)
コンデンサの定格容量が\( \ Q_{\mathrm {n}}=50 \ \mathrm {[kvar]} \ \)，定格電圧が\( \ V_{\mathrm {n}}=6.6 \ \mathrm {[kV]} \ \)であるから，コンデンサの定格電流\( \ I_{\mathrm {n}} \ \)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {n}} &=& \frac {Q_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=& \frac {50\times 10^{3}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ] &≒& 4.374 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。図1より，\( \ \mathrm {R} \ \)相の電流\( \ I_{\mathrm {R}} \ \)の大きさは\( \ I_{\mathrm {R}}=1.50 I_{\mathrm {n}} \ \)，\( \ \mathrm {S} \ \)相及び\( \ \mathrm {T} \ \)相の電流\( \ I_{\mathrm {S}} \ \)及び\( \ I_{\mathrm {T}} \ \)の大きさは\( \ I_{\mathrm {S}}=I_{\mathrm {T}}=1.15 I_{\mathrm {n}} \ \)であるから，
\[
\begin{eqnarray}
I_{\mathrm {R}} &=& 1.50 I_{\mathrm {n}} \\[ 5pt ] &=& 1.50 \times 4.374 \\[ 5pt ] &≒& 6.561　→　6.6 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {S}} &=& I_{\mathrm {T}}=1.15 \ I_{\mathrm {n}} \\[ 5pt ] &=& 1.15 \times 4.374 \\[ 5pt ] &≒& 5.030　→　5.0 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
高圧進相コンデンサの\( \ 1 \ \)素子の静電容量を\( \ C \ \)とする。
内部素子短絡が\( \ \mathrm {R} \ \)相のコンデンサに発生しているので，\( \ \mathrm {R－S} \ \)相間の静電容量を\( \ C_{\mathrm {RS}} \ \)，\( \ \mathrm {S－T} \ \)相間の静電容量を\( \ C_{\mathrm {ST}} \ \)，\( \ \mathrm {T－R} \ \)相間の静電容量を\( \ C_{\mathrm {TR}} \ \)とすると，
\[
\begin{eqnarray}
\frac {1}{C_{\mathrm {RS}}} &=& \frac {1}{C}+\frac {1}{C}+\frac {1}{C} \\[ 5pt ] C_{\mathrm {RS}}&=& \frac {C}{3} \\[ 5pt ] \frac {1}{C_{\mathrm {ST}}} &=& \frac {1}{C}+\frac {1}{C}+\frac {1}{C}+\frac {1}{C} \\[ 5pt ] C_{\mathrm {ST}}&=& \frac {C}{4} \\[ 5pt ] \frac {1}{C_{\mathrm {TR}}} &=& \frac {1}{C}+\frac {1}{C}+\frac {1}{C} \\[ 5pt ] C_{\mathrm {TR}}&=& \frac {C}{3} \\[ 5pt ] \end{eqnarray}
\] となる。これより，正しい選択肢は(2)となる。