《法規》〈電気施設管理〉[R06上:問11]力率改善に伴う電圧降下の変化に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

変電所から三相\( \ 3 \ \)線式\( \ 1 \ \)回線の専用配電線で受電している需要家がある。この配電線路の電線\( \ 1 \ \)条当たりの抵抗及びリアクタンスの値は，それぞれ\( \ 3 \ \mathrm {\Omega } \ \)及び\( \ 5 \ \mathrm {\Omega } \ \)である。この需要家の使用電力が\( \ 8 \ 000 \ \mathrm {kW} \ \)，負荷の力率が\( \ 0.8 \ \)（遅れ）であるとき，次の(a)及び(b)の問に答えよ。

(a)　需要家の受電電圧が\( \ 20 \ \mathrm {kV} \ \)のとき，変電所引出口の電圧\( \ \mathrm {[kV]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 21.6 \ \)　　(2)　\( \ 22.2 \ \)　　(3)　\( \ 22.7 \ \)　　(4)　\( \ 22.9 \ \)　　(5)　\( \ 23.1 \ \)

(b)　需要家にコンデンサを設置して，負荷の力率を\( \ 0.95 \ \)（遅れ）に改善するとき，この配電線の電圧降下の値\( \ \mathrm {[V]} \ \)の，コンデンサ設置前の電圧降下の値\( \ \mathrm {[V]} \ \)に対する比率\( \ \mathrm {[％]} \ \)の値として，最も近いのは次のうちどれか。

ただし，この需要家の受電電圧\( \ \mathrm {[kV]} \ \)は，コンデンサ設置前と同一の\( \ 20 \ \mathrm {kV} \ \)とする。

　(1)　\( \ 66.6 \ \)　　(2)　\( \ 68.8 \ \)　　(3)　\( \ 75.5 \ \)　　(4)　\( \ 81.7 \ \)　　(5)　\( \ 97.0 \ \)

【ワンポイント解説】

需要家にコンデンサを接続したときの電圧変化に関する問題です。
解法パターンが同じなので，(a)が解けた方が(b)も解ける非常に厳しい問題となります。
電力科目でも出題される重要な内容なので，必ず理解するようにしましょう。
本問はやや古いですが平成15年問12からの再出題となります。

1.配電線の電圧降下の近似式
①単相\( \ 2 \ \)線式配電線の電圧降下
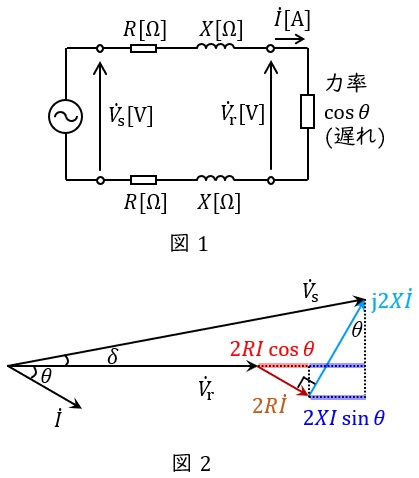
単相\( \ 2 \ \)線式線路は図1のような回路になり，負荷に対して供給される線路と戻りの線路の\( \ 2 \ \)段階で電圧降下が発生します。したがって，負荷の力率が遅れ力率\( \ \cos \theta \ \)であるときのベクトル図を描くと図2のようになります。
図2のベクトル図において，\( \ {\dot V}_{\mathrm {s}} \ \)と\( \ {\dot V}_{\mathrm {r}} \ \)の位相差が十分に小さいと仮定すると，線路の電圧降下\( \ \varepsilon =V_{\mathrm {s}}-V_{\mathrm {r}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {s}}&≃&V_{\mathrm {r}}+2RI\cos \theta +2XI\sin \theta \\[ 5pt ] V_{\mathrm {s}}-V_{\mathrm {r}}&=&2RI\cos \theta +2XI\sin \theta \\[ 5pt ] \varepsilon &=&2I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] と求められます。

②三相\( \ 3 \ \)線式配電線の電圧降下
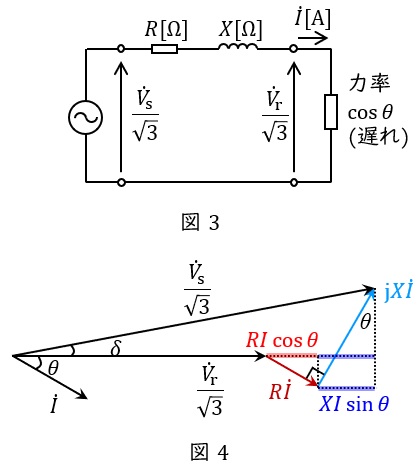
三相回路においては，一相分の等価回路及びベクトル図は図3及び図4のように描くことができ，三相分の電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&≃&\frac {V_{\mathrm {r}}}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ] \frac {V_{\mathrm {s}}}{\sqrt {3}}-\frac {V_{\mathrm {r}}}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ] V_{\mathrm {s}}-V_{\mathrm {r}}&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ] \varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

(a)解答：(3)
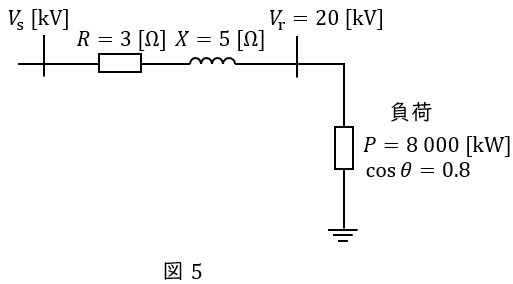
題意に沿って単線図を描くと図5のようになる。
需要家の使用電力が\( \ P=8 \ 000 \ \mathrm {[kW]} \ \)であることから，負荷電流の大きさ\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
P&=&\sqrt {3}V_{\mathrm {r}}I\cos \theta \\[ 5pt ] I&=&\frac {P}{\sqrt {3}V_{\mathrm {r}}\cos \theta } \\[ 5pt ] &=&\frac {8 \ 000\times 10^{3}}{\sqrt {3}\times 20\times 10^{3}\times 0.8} \\[ 5pt ] &≒&288.7 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \sin ^{2}\theta +\cos ^{2}\theta =1 \ \)より，負荷の\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-0.8^{2}} \\[ 5pt ] &=&0.6 \\[ 5pt ] \end{eqnarray}
\] となる。これより，線路での電圧降下\( \ \varepsilon \ \mathrm {[kV]} \ \)は，ワンポイント解説「1.配電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] &=&\sqrt {3}\times 288.7\times \left( 3\times 0.8 +5\times 0.6 \right) \\[ 5pt ] &≒&2 \ 700 \ \mathrm {[V]}　→　2.700 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となるので，変電所引出口の電圧\( \ V_{\mathrm {s}} \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {s}}&=&V_{\mathrm {r}}+\varepsilon \\[ 5pt ] &=&20+2.700 \\[ 5pt ] &=&22.7 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
負荷の力率\( \ \cos \theta ^{\prime }=0.95 \ \)のときの負荷電流の大きさ\( \ I^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
P&=&\sqrt {3}V_{\mathrm {r}}I^{\prime }\cos \theta ^{\prime } \\[ 5pt ] I^{\prime }&=&\frac {P}{\sqrt {3}V_{\mathrm {r}}\cos \theta ^{\prime }} \\[ 5pt ] &=&\frac {8 \ 000\times 10^{3}}{\sqrt {3}\times 20\times 10^{3}\times 0.95} \\[ 5pt ] &≒&243.1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，負荷の\( \ \sin \theta ^{\prime } \ \)は，
\[
\begin{eqnarray}
\sin \theta ^{\prime } &=&\sqrt {1-\cos ^{2}\theta ^{\prime } } \\[ 5pt ] &=&\sqrt {1-\cos ^{2}\theta ^{\prime } } \\[ 5pt ] &=&\sqrt {1-0.95^{2}} \\[ 5pt ] &≒&0.312 \ 2 \\[ 5pt ] \end{eqnarray}
\] となる。これより，線路での電圧降下\( \ \varepsilon ^{\prime } \ \mathrm {[V]} \ \)は，ワンポイント解説「1.配電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
\varepsilon ^{\prime }&=&\sqrt {3}I\left( R\cos \theta ^{\prime } +X\sin \theta ^{\prime } \right) \\[ 5pt ] &=&\sqrt {3}\times 243.1\times \left( 3\times 0.95 +5\times 0.312 \ 2 \right) \\[ 5pt ] &≒&1 \ 857 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，コンデンサ接続前後の電圧降下の比は，
\[
\begin{eqnarray}
\frac {\varepsilon ^{\prime }}{\varepsilon }&=&\frac {1 \ 857}{2 \ 700} \\[ 5pt ] &≒&0.688　→　68.8 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。