Contents
【問題】
【難易度】★★★☆☆(普通)
\( \ 2 \ \)進数\( \ A \ \),\( \ B \ \)が,\( \ A=\left( 1100 \ 0011 \right) _{2} \ \),\( \ B=\left( 1010 \ 0101 \right) _{2} \ \)であるとき,\( \ A \ \)と\( \ B \ \)のビットごとの論理演算を考える。\( \ A \ \)と\( \ B \ \)の論理積\( \ \left( \mathrm {AND} \right) \ \)を\( \ 16 \ \)進数で表すと\( \ \fbox { (ア) } \ \),\( \ A \ \)と\( \ B \ \)の論理和\( \ \left( \mathrm {OR} \right) \ \)を\( \ 16 \ \)進数で表すと\( \ \fbox { (イ) } \ \),\( \ A \ \)と\( \ B \ \)の排他的論理和\( \ \left( \mathrm {EX-OR} \right) \ \)を\( \ 16 \ \)進数で表すと\( \ \fbox { (ウ) } \ \),\( \ A \ \)と\( \ B \ \)の否定的論理積\( \ \left( \mathrm {NAND} \right) \ \)を\( \ 16 \ \)進数で表すと\( \ \fbox { (エ) } \ \)となる。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる数値として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & \left( 81 \right) _{16} & \left( \mathrm {E}7 \right) _{16} & \left( 66 \right) _{16} & \left( 18 \right) _{16} \\
\hline
(2) & \left( 81 \right) _{16} & \left( \mathrm {E}7 \right) _{16} & \left( 66 \right) _{16} & \left( 7\mathrm {E} \right) _{16} \\
\hline
(3) & \left( 81 \right) _{16} & \left( \mathrm {E}7 \right) _{16} & \left( 99 \right) _{16} & \left( 18 \right) _{16} \\
\hline
(4) & \left( \mathrm {E}7 \right) _{16} & \left( 81 \right) _{16} & \left( 66 \right) _{16} & \left( 7\mathrm {E} \right) _{16} \\
\hline
(5) & \left( \mathrm {E}7 \right) _{16} & \left( 81 \right) _{16} & \left( 99 \right) _{16} & \left( 18 \right) _{16} \\
\hline
\end{array}
\]
【ワンポイント解説】
論理回路の演算と進数の変換の両方の知識を問う問題です。
非常に出題頻度の高い分野となるため,確実に理解し,できれば素早く解けるようになりましょう。このままの再出題も十分想定される問題かと思います。
1.主な論理回路の真理値表
基本的な論理回路と図記号は覚える必要がありますので,以下の真理値表を覚えておきましょう。
①\( \ \mathrm {AND} \ \)回路
論理積といい,すべての入力が\( \ 1 \ \)の時のみ\( \ 1 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
1 & 1 & 1 \\
\end{array}
\]

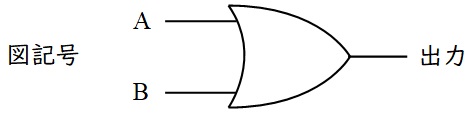
②\( \ \mathrm {OR} \ \)回路
論理和といい,入力が一つでも\( \ 1 \ \)の時\( \ 1 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1 \\
\end{array}
\]
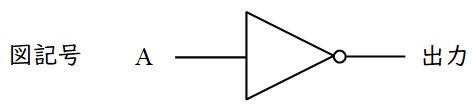
③\( \ \mathrm {NOT} \ \)回路
論理否定といい,入力を反転する回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{c|c}
\mathrm {A} & 出力 \\
\hline
0 & 1 \\
1 & 0 \\
\end{array}
\]
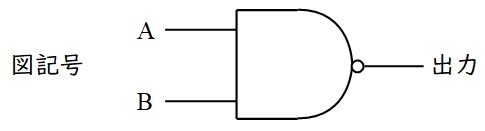
④\( \ \mathrm {NAND} \ \)回路
\( \ \mathrm {NOT}+\mathrm {AND} \ \)で\( \ \mathrm {AND} \ \)の\( \ \mathrm {NOT} \ \)を出力,すなわちすべての入力が\( \ 1 \ \)の時のみ\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 1 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\
\end{array}
\]
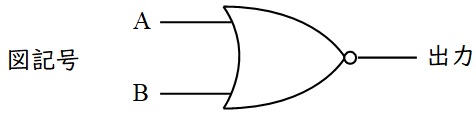
⑤\( \ \mathrm {NOR} \ \)回路
\( \ \mathrm {NOT}+\mathrm {OR} \ \)で\( \ \mathrm {OR} \ \)の\( \ \mathrm {NOT} \ \)を出力,すなわち入力が一つでも\( \ 1 \ \)の時\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
1 & 1 & 0 \\
\end{array}
\]
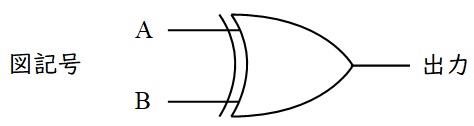
⑥\( \ \mathrm {ExOR} \ \)回路
排他的論理和\( \ \left( \mathrm {exclusive \ or} \right) \ \)といい,入力が異なるとき\( \ 1 \ \),入力が同じ時\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\
\end{array}
\]
2.主な進数の対応表
コンピュータ等のディジタル信号は主に\( \ 2 \ \)進数が使用されるため,電験でも基数変換は出題されます。
電験で出題される\( \ 2 \ \)進数,\( \ 8 \ \)進数,\( \ 10 \ \)進数,\( \ 16 \ \)進数の対応表は下表の通りとなります。表を覚えるのではなくルールを理解するようにしましょう。
\[
\begin{array}{|r|r|r|r|}
\hline
2 \ 進数 & 8 \ 進数 & 10 \ 進数 & 16 \ 進数 \\
\hline
0 & 0 & 0 & 0 \\
\hline
1 & 1 & 1 & 1 \\
\hline
10 & 2 & 2 & 2 \\
\hline
11 & 3 & 3 & 3 \\
\hline
100 & 4 & 4 & 4 \\
\hline
101 & 5 & 5 & 5 \\
\hline
110 & 6 & 6 & 6 \\
\hline
111 & 7 & 7 & 7 \\
\hline
1000 & 10 & 8 & 8 \\
\hline
1001 & 11 & 9 & 9 \\
\hline
1010 & 12 & 10 & \mathrm {A} \\
\hline
1011 & 13 & 11 & \mathrm {B} \\
\hline
1100 & 14 & 12 & \mathrm {C} \\
\hline
1101 & 15 & 13 & \mathrm {D} \\
\hline
1110 & 16 & 14 & \mathrm {E} \\
\hline
1111 & 17 & 15 & \mathrm {F} \\
\hline
10000 & 20 & 16 & 10 \\
\hline
\end{array}
\]
3.\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換
\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換は,\( \ 2 \ \)で割った余りを下から順に並べると求められます。
具体的に\( \ 10 \ \)進数の\( \ \left( 30\right) _{10} \ \)を\( \ 2 \ \)進数へ変換すると,
\[
\begin{array}{cccc}
2) & 30 & & & \\
\hline
2) & 15 & \cdots & 0 \\
\hline
2) & 7 & \cdots & 1 \\
\hline
2) & 3 & \cdots & 1 \\
\hline
2) & 1 & \cdots & 1 \\
\hline
& 0 & \cdots & 1 \\
\end{array}
\]
ゆえに,
\[
\begin{eqnarray}
\left( 30\right) _{10} &=&\left( 11110\right) _{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ 8 \ \)進数や\( \ 16 \ \)進数への変換も同様に行うことができます。
4.\( \ 2 \ \)進数から\( \ 10 \ \)進数への変換
\( \ 2 \ \)進数を\( \ 10 \ \)進数にするためには各桁に\( \ 2^{x}(x=0,1,2・・・) \ \)乗をかけて導出できます。
例えば,\( \ 2 \ \)進数の\( \ \left( 101010\right) _{2} \ \)を\( \ 10 \ \)進数へ変換すると,
\[
\begin{eqnarray}
\left( 101010\right) _{2}&=&1\times 2^{5}+0\times 2^{4}+1\times 2^{3}+0\times 2^{2}+1\times 2^{1}+0\times 2^{0} \\[ 5pt ]
&=&32+0+8+0+2+0 \\[ 5pt ]
&=&42 \\[ 5pt ]
\end{eqnarray}
\]
と求められます。\( \ 8 \ \)進数や\( \ 16 \ \)進数も同様に求められます。
5.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換
\( \ 2 \ \)進数を\( \ 16 \ \)進数にするためには,\( \ 4 \ \)桁ごとに\( \ 16 \ \)進数に変換していきます。
例えば,\( \ 2 \ \)進数の\( \ \left( 11011010\right) _{2} \ \)を\( \ 16 \ \)進数へ変換すると,
\[
\begin{eqnarray}
\left( 1101\right) _{2}&=&\left( \mathrm {D}\right) _{16} \\[ 5pt ]
\left( 1010\right) _{2}&=&\left( \mathrm {A}\right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\left( 11011010\right) _{2}&=&\left( \mathrm {DA}\right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。\( \ 16 \ \)進数から\( \ 2 \ \)進数への変換も逆の操作により求めることができます。
【解答】
解答:(2)
(ア)
\( \ A \ \)と\( \ B \ \)の論理積\( \ A\cdot B \ \)は,ワンポイント解説「1.主な論理回路の真理値表」の通り,
\[
\begin{eqnarray}
A\cdot B&=&\left( 1000 \ 0001 \right) _{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを\( \ 16 \ \)進数に変換すると,ワンポイント解説「2.主な進数の対応表」及び「5.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
A\cdot B&=&\left( 81 \right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(イ)
\( \ A \ \)と\( \ B \ \)の論理和\( \ A+B \ \)は,ワンポイント解説「1.主な論理回路の真理値表」の通り,
\[
\begin{eqnarray}
A+B&=&\left( 1110 \ 0111 \right) _{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを\( \ 16 \ \)進数に変換すると,ワンポイント解説「2.主な進数の対応表」及び「5.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
A+B&=&\left( \mathrm {E} 7 \right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(ウ)
\( \ A \ \)と\( \ B \ \)の排他的論理和\( \ A⊕B \ \)は,ワンポイント解説「1.主な論理回路の真理値表」の通り,
\[
\begin{eqnarray}
A⊕B&=&\left( 0110 \ 0110 \right) _{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを\( \ 16 \ \)進数に変換すると,ワンポイント解説「2.主な進数の対応表」及び「5.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
A⊕B&=&\left( 66 \right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(エ)
\( \ A \ \)と\( \ B \ \)の否定的論理積\( \ \overline {A\cdot B} \ \)は,ワンポイント解説「1.主な論理回路の真理値表」の通り,
\[
\begin{eqnarray}
\overline {A\cdot B}&=&\left( 0111 \ 1110 \right) _{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを\( \ 16 \ \)進数に変換すると,ワンポイント解説「2.主な進数の対応表」及び「5.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
A\cdot B&=&\left( 7\mathrm {E} \right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは