Contents
【問題】
【難易度】★★★☆☆(普通)
温度\( \ 20.0 \ \mathrm {[℃]} \ \),体積\( \ 0.370 \ \mathrm {[m^{3}]} \ \)の水の温度を\( \ 90.0 \ \mathrm {[℃]} \ \)まで上昇させたい。次の(a)及び(b)に答えよ。
ただし,水の比熱(比熱容量)と密度はそれぞれ\( \ 4.18 \times 10^{3} \ \mathrm {[J / (kg \cdot K)]} \ \),\( \ 1.00 \times 10^{3} \ \mathrm {[kg / m^{3}]} \ \)とし,水の温度に関係なく一定とする。
(a) 電熱器容量\( \ 4.44 \ \mathrm {[kW]} \ \)の電気温水器を使用する場合,これに必要な時間\( \ t \ \mathrm {[h]} \ \)の値として,最も近いのは次のうちどれか。
ただし,貯湯槽を含む電気温水器の総合効率は\( \ 90.0 \ \mathrm {[%]} \ \)とする。
(1) \( \ 3.15 \ \) (2) \( \ 6.10 \ \) (3) \( \ 7.53 \ \) (4) \( \ 8.00 \ \) (5) \( \ 9.68 \ \)
(b) 上記(a)の電気温水器の代わりに,最近普及してきた自然冷媒\( \ \left( \mathrm {CO_{2}} \right) \ \)ヒートポンプ式電気給湯器を使用した場合,これに必要な時間\( \ t \ \mathrm {[h]} \ \)は,消費電力\( \ 1.25 \ \mathrm {[kW]} \ \)で\( \ 6 \ \mathrm {[h]} \ \)であった。水が得たエネルギーと消費電力量とで表せるヒートポンプユニットの成績係数\( \ \left( \mathrm {COP} \right) \ \)の値として,最も近いのは次のうちどれか。
ただし,ヒートポンプユニット及び貯湯槽の電力損,熱損失はないものとする。
(1) \( \ 0.25 \ \) (2) \( \ 0.33 \ \) (3) \( \ 3.01 \ \) (4) \( \ 4.01 \ \) (5) \( \ 4.19 \ \)
【ワンポイント解説】
水を温めるのに必要な時間とヒートポンプユニットの成績係数を求める問題です。
(a)の方が計算量が多く,(b)も(a)が解けないと正答できない問題なので,点数差が拡がりやすい問題です。
このような水の温度上昇の問題は,電験の参考書に掲載されている公式を丸暗記するのではなく,一つ一つの公式をしっかりと理解していくことが重要となります。
1.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換
単位の定義より,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ/s]} &=&1 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,両辺の単位に\( \ \mathrm {[s]} \ \)をかけると,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot s]} \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺に\( \ 1 \ \mathrm {[h]}=3600 \ \mathrm {[s]} \ \)を考慮して,\( \ 3600 \ \)をかけると,
\[
\begin{eqnarray}
3 \ 600 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.ヒートポンプの構成機器
ヒートポンプのフローを図1に示します。冷房時が青線,暖房時は赤線の流れとなります。冷房時を例に示します。
蒸発器:膨張弁からの低温低圧の液を蒸発させ気化させます。
四方弁:暖房冷房時に圧縮機に流れる媒体の向きを同じにするために向きを変えるものです。
圧縮機:蒸発器から出た低圧の蒸気を高圧蒸気にします。
凝縮器:圧縮機で高温高圧となった蒸気を凝縮し,液化させます。
膨張弁:凝縮器から出た液を膨張し,低温低圧の液にします。
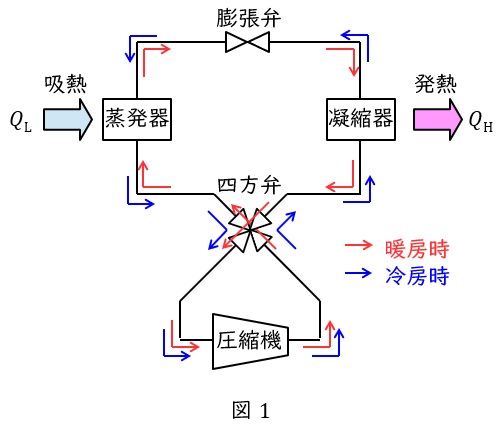
※図1において,暖房時には熱交換器である蒸発器と凝縮器の役割が逆となります。
3.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))
図1において,蒸発器の吸熱量\( \ Q_{\mathrm {L}} \ \)及び圧縮機にかける仕事量\( \ W \ \)と凝縮器の放熱量\( \ Q_{\mathrm {H}} \ \)は等しいので,
\[
\begin{eqnarray}
Q_{\mathrm {H}}&=&Q_{\mathrm {L}}+W \\[ 5pt ]
\end{eqnarray}
\]
という関係があり,冷房時と暖房時の成績係数\( \ \mathrm {{COP}_{L}} \ \),\( \ \mathrm {{COP}_{H}} \ \)は,
\[
\begin{eqnarray}
\mathrm {{COP}_{L}}&=&\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ]
\mathrm {{COP}_{H}}&=&\frac {Q_{\mathrm {H}}}{W} \\[ 5pt ]
&=&\frac {Q_{\mathrm {L}}+W}{W} \\[ 5pt ]
&=&1+\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.水の温度上昇と必要なエネルギーの関係
水にエネルギー\( \ Q \ \mathrm {[J]} \ \)を加えたときの温度上昇値\( \ \Delta T \ \mathrm {[K]} \ \)には,質量\( \ m \ \mathrm {[kg]} \ \),比熱容量\( \ c \ \mathrm {[J / \left( kg\cdot K\right) ]} \ \)とすると
\[
\begin{eqnarray}
Q &=&mc \Delta T \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(a)解答:(3)
水の質量\( \ m \ \mathrm {[kg]} \ \)は,水の体積\( \ V=0.370 \ \mathrm {[m^{3}]} \ \),水の密度が\( \ \rho =1.00\times 10^{3} \ \mathrm {[kg / m^{3}]} \ \)であることから,
\[
\begin{eqnarray}
m &=&\rho V \\[ 5pt ]
&=&1.00\times 10^{3} \times 0.370 \\[ 5pt ]
&=&370 \ \mathrm {[kg]} \\[ 5pt ]
\end{eqnarray}
\]
となり,比熱(比熱容量)が\( \ c=4.18 \times 10^{3} \ \mathrm {[J / \left( kg\cdot K\right) ]} \ \),温度上昇が\( \ \Delta T=90.0 -20.0=70.0 \ \mathrm {[K]} \ \)であることから,温めるのに必要な熱量\( \ Q \ \mathrm {[kJ]} \ \)は,ワンポイント解説「4.水の温度上昇と必要なエネルギーの関係」の通り,
\[
\begin{eqnarray}
Q &=&mc \Delta T \\[ 5pt ]
&=&370\times 4.18 \times 10^{3} \times 70 \\[ 5pt ]
&≒&108 \ 300 \ 000 \mathrm {[J]} → 108 \ 300 \ \mathrm {[kJ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ Q=108 \ 300 \ \mathrm {[kJ]} \ \)を電力量換算した値\( \ W \ \mathrm {[kW\cdot h]} \ \)は,ワンポイント解説「1.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換」の通り,
\[
\begin{eqnarray}
W &=&\frac {Q}{3 \ 600} \\[ 5pt ]
&=&\frac {108 \ 300}{3 \ 600} \\[ 5pt ]
&≒&30.08 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,電熱器容量\( \ P=4.44 \ \mathrm {[kW]} \ \),効率\( \ \eta =0.90 \ \)の電気温水器を使用する場合に,温めるのに必要な時間\( \ t \ \mathrm {[h]} \ \)は,
\[
\begin{eqnarray}
W &=&P\eta t \\[ 5pt ]
t&=&\frac {W}{P\eta } \\[ 5pt ]
&=&\frac {30.08}{4.44 \times 0.90} \\[ 5pt ]
&≒&7.53 \ \mathrm {[h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
ヒートポンプ式電気給湯器の入力電力量\( \ W_{\mathrm {i}} \ \mathrm {[kW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {i}} &=&1.25\times 6 \\[ 5pt ]
&=&7.5 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
なので,成績係数\( \ \mathrm {COP} \ \)は,
\[
\begin{eqnarray}
\mathrm {COP} &=&\frac {W}{W_{\mathrm {i}}} \\[ 5pt ]
&=&\frac {30.08}{7.5} \\[ 5pt ]
&≒&4.01 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは