Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,巻線形誘導電動機に関する記述である。
三相巻線形誘導電動機の二次側に外部抵抗を接続して,誘導電動機を運転することを考える。ただし,外部抵抗は誘導電動機内の二次回路にある抵抗に比べて十分大きく,誘導電動機内部の鉄損,銅損及び一次,二次のインダクタンスなどは無視できるものとする。
いま,回転子を拘束して,一次電圧\( \ V_{\mathrm {1}} \ \)として\( \ 200 \ \mathrm {[V]} \ \)を印加したときに二次側の外部抵抗を接続した端子に現れる電圧\( \ V_{\mathrm {2s}} \ \)は\( \ 140 \ \mathrm {[V]} \ \)であった。拘束を外して始動した後に回転速度が上昇し,同期速度\( \ 1 \ 500 \ \mathrm {[min^{-1}]} \ \)に対して\( \ 1 \ 200 \ \mathrm {[min^{-1}]} \ \)に到達して,負荷と釣り合ったとする。
このときの一次電圧\( \ V_{\mathrm {1}} \ \)は\( \ 200 \ \mathrm {[V]} \ \)のままであると,二次側の端子に現れる電圧\( \ V_{\mathrm {2}} \ \)は\( \ \fbox { (ア) } \ \mathrm {[V]} \ \)となる。
また,機械負荷に\( \ P_{\mathrm {m}} \ \mathrm {[W]} \ \)が伝達されるとすると,一次側から供給する電力\( \ P_{\mathrm {1}} \ \mathrm {[W]} \ \),外部抵抗で消費される電力\( \ P_{\mathrm {2c}} \ \mathrm {[W]} \ \)との関係は次式となる。
\[
\begin{eqnarray}
P_{\mathrm {1}} &=&P_{\mathrm {m}}+ \ \fbox { (イ) } \ \times P_{\mathrm {2c}} \\[ 5pt ]
P_{\mathrm {2c}} &=& \ \fbox { (ウ) } \ \times P_{\mathrm {1}} \\[ 5pt ]
\end{eqnarray}
\]
したがって,\( \ P_{\mathrm {2c}} \ \)と\( \ P_{\mathrm {m}} \ \)の関係は次式となる。
\[
\begin{eqnarray}
P_{\mathrm {2c}} &=& \ \fbox { (エ) } \ \times P_{\mathrm {m}} \\[ 5pt ]
\end{eqnarray}
\]
接続する外部抵抗には,このような運転に使える電圧・容量の抵抗器を選択しなければならない。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 112 & 0.8 & 0.8 & 0.25 \\
\hline
(2) & 28 & 1 & 0.2 & 4 \\
\hline
(3) & 28 & 1 & 0.2 & 0.25 \\
\hline
(4) & 112 & 0.8 & 0.8 & 4 \\
\hline
(5) & 112 & 1 & 0.2 & 0.25 \\
\hline
\end{array}
\]
【ワンポイント解説】
誘導電動機の入力や出力,損失の関係に関する問題です。
意外と\( \ \fbox { (ア) } \ \)の空欄の関係を知らない受験生が多く,正答率は低かったのではないかと思われる問題です。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \),回転数が\( \ N \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
で定義され,上式を変形すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&N_{\mathrm {s}}\left( 1-s\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.二次周波数(滑り周波数)\( \ f_{2} \ \),二次誘導起電力\( \ E_{2}^{\prime } \ \)
誘導電動機の固定子を一次回路,回転子を二次回路といい,固定子(回転磁界)の回転速度が\( \ N_{\mathrm {s}} \ \),回転子の回転数が\( \ N \ \)であるとき,相対速度\( \ \Delta N \ \)は,
\[
\begin{eqnarray}
\Delta N &=&N_{\mathrm {s}}-N \\[ 5pt ]
&=&sN_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
となります。回転子に発生する二次周波数(滑り周波数)\( \ f_{2} \ \)は,回転速度が周波数に比例することから,電源周波数を\( \ f \ \)とすると,
\[
\begin{eqnarray}
f_{2} &=&sf \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導起電力\( \ E \ \)が周波数に比例することから,二次誘導起電力\( \ E_{2}^{\prime } \ \)は,静止時の二次誘導起電力を\( \ E_{2} \ \)とすると,
\[
\begin{eqnarray}
E_{2}^{\prime } &=&sE_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求めることができます。
4.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
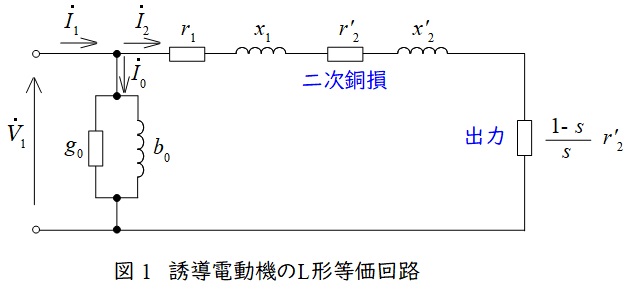
誘導電動機のL形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \)は一次電流,\( \ {\dot I}_{2} \ \)は二次電流,\( \ {\dot I}_{0} \ \)は励磁電流,\( \ r_{1} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \),二次入力\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=&3 \frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }I_{2}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \),出力\( \ P_{\mathrm {o}} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
【解答】
解答:(3)
(ア)
拘束を外して回転速度を上昇した後の誘導電動機の滑り\( \ s \ \)は,ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {1500-1200}{1500} \\[ 5pt ]
&=&0.2 \\[ 5pt ]
\end{eqnarray}
\]
であり,回転子を拘束したときに現れる電圧\( \ V_{\mathrm {2s}} = 140 \ \mathrm {[V]} \ \)であるから,二次側の端子に現れる電圧\( \ V_{\mathrm {2}} \ \)は,ワンポイント解説「3.二次周波数(滑り周波数)\( \ f_{2} \ \),二次誘導起電力\( \ E_{2}^{\prime } \ \)」の通り,
\[
\begin{eqnarray}
V_{\mathrm {2}} &=&sV_{\mathrm {2s}} \\[ 5pt ]
&=&0.2\times 140 \\[ 5pt ]
&=&28 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(イ)
題意より,「誘導電動機内部の鉄損,銅損及び一次,二次のインダクタンスなどは無視できる」となっているので,供給する電力\( \ P_{\mathrm {1}} \ \mathrm {[W]} \ \)は機械負荷\( \ P_{\mathrm {m}} \ \mathrm {[W]} \ \)と外部抵抗\( \ P_{\mathrm {2c}} \ \mathrm {[W]} \ \)に全て供給されることになる。したがって,
\[
\begin{eqnarray}
P_{\mathrm {1}} &=&P_{\mathrm {m}}+P_{\mathrm {2c}} \\[ 5pt ]
&=&P_{\mathrm {m}}+1\times P_{\mathrm {2c}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(ウ)
本問の場合,一次銅損は無視できるので,一次入力\( \ P_{\mathrm {1}} \ \mathrm {[W]} \ \)と二次入力\( \ P_{\mathrm {2}} \ \mathrm {[W]} \ \)は等しいと考えることができる。ワンポイント解説「4.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」の通り,
\[
\begin{eqnarray}
P_{\mathrm {1}}\left( =P_{2}\right) :P_{\mathrm {m}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,
\[
\begin{eqnarray}
P_{\mathrm {2c}} &=&sP_{\mathrm {1}} \\[ 5pt ]
&=&0.2\times P_{\mathrm {1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(エ)
(ウ)と同様に,
\[
\begin{eqnarray}
\frac {P_{\mathrm {2c}}}{P_{\mathrm {m}}} &=&\frac {s}{1-s} \\[ 5pt ]
&=&\frac {0.2}{1-0.2} \\[ 5pt ]
&=&0.25 \\[ 5pt ]
P_{\mathrm {2c}}&=&0.25\times P_{\mathrm {m}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは