《機械》〈回転機〉[H25:問2]直流発電機の誘導起電力に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図は，磁極数が\( \ 2 \ \)の直流発電機を模式的に表したものである。電機子巻線については，\( \ 1 \ \)巻き分のコイルを示している。電機子の直径\( \ D \ \)は\( \ 0.5 \ \mathrm {[m]} \ \)，電機子導体の有効長\( \ l \ \)は\( \ 0.3 \ \mathrm {[m]} \ \)，ギャップの磁束密度\( \ B \ \)は，図の状態のように電機子導体が磁極の中心付近にあるとき一定で\( \ 0.4 \ \mathrm {[T]} \ \)，回転速度\( \ n \ \)は\( \ 1200 \ \mathrm {[{min} ^{-1}]} \ \)である。図の状態におけるこの\( \ 1 \ \)巻きのコイルに誘導される起電力\( \ e \ \mathrm {[V]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

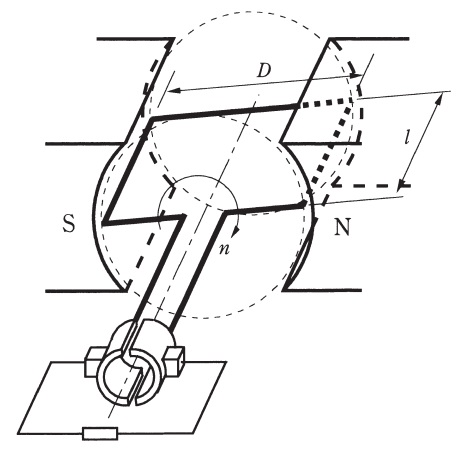
　(1)　\( \ 2.40 \ \)　　(2)　\( \ 3.77 \ \)　　(3)　\( \ 7.54 \ \)　　(4)　\( \ 15.1 \ \)　　(5)　\( \ 452 \ \)

【ワンポイント解説】

理論科目の範囲であるフレミングの右手の法則を理解していること，回転速度と直径から速度を求めること，の２点の知識が必要です。物理的な内容と数学的な内容の両方を知っていないと解けないため，若干応用的な問題となりますが，発電機の原理を理解するには非常に良い問題と言えると思います。

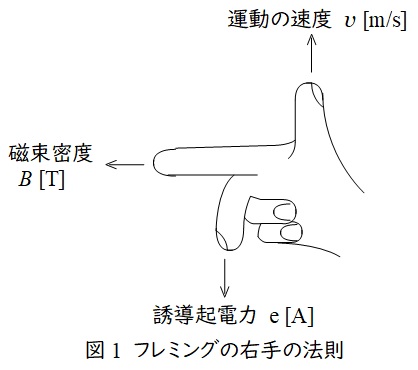
1.フレミングの右手の法則
親指を導体の運動方向，人差し指を磁界（磁束密度）の方向にすると，中指の方向に誘導起電力が発生するという法則で，磁束密度の大きさを\( \ B \ \mathrm {[T]} \ \)，導体の速度を\( \ v \ \mathrm {[m／s]} \ \)，導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，誘導起電力の大きさ\( \ e \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
e &=& Blv \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
コイルの運動速度\( \ v \ \)は，コイルの半径を\( \ \displaystyle r=\frac {D}{2} \ \)，角速度を\( \ \displaystyle \omega =\frac {2\pi n}{60} \ \)とすると，
\[
\begin{eqnarray}
v &=& r\omega \\[ 5pt ] &=& \frac {D}{2}\cdot \frac {2\pi n}{60} \\[ 5pt ] &=& \frac {\pi Dn}{60} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説より，\( \ \displaystyle e=Blv \ \)であり，コイルの有効長は\( l \)の２本分であるから，
\[
\begin{eqnarray}
e &=& B\cdot 2l\cdot v \\[ 5pt ] &=& B\cdot 2l\cdot \frac {\pi Dn}{60} \\[ 5pt ] &=& \frac {Bl\pi Dn}{30} \\[ 5pt ] &=& \frac {0.4\times 0.3\times \pi \times 0.5\times 1200}{30} \\[ 5pt ] &≒& 7.54 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。