Contents
【問題】
【難易度】★★★☆☆(普通)
二次電流一定(トルクがほぼ一定の負荷条件)で運転している三相巻線形誘導電動機がある。滑り\( \ 0.01 \ \)で定格運転しているときに,二次回路の抵抗を大きくしたところ,二次回路の損失は\( \ 30 \ \)倍に増加した。電動機の出力は定格出力の何\( \ \mathrm {[%]} \ \)になったか,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 10 \ \) (2) \( \ 30 \ \) (3) \( \ 50 \ \) (4) \( \ 70 \ \) (5) \( \ 90 \ \)
【ワンポイント解説】
誘導電動機の二次抵抗と出力の関係に関する問題です。等価回路を描いて等価回路からトルクを導出して比例推移の関係を導き出すことも可能ですが,計算が複雑となり時間もかかってしまうので,試験時には比例推移の関係の公式を暗記しておいた方が良いと思います。
1.誘導電動機の二次回路の入力,出力,損失の関係
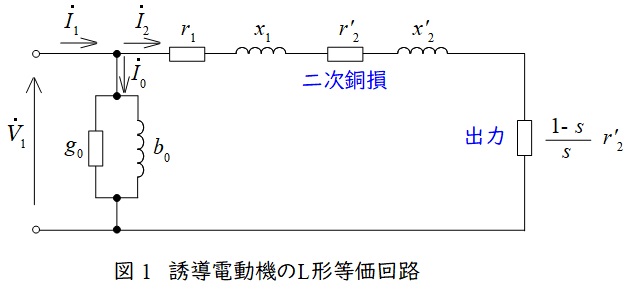
誘導電動機のL形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \)は一次電流,\( \ {\dot I}_{2} \ \)は二次電流,\( \ {\dot I}_{0} \ \)は励磁電流,\( \ r_{1} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \),二次入力\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& \frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& r_{2}^{\prime }I_{2}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \),出力\( \ P_{\mathrm {o}} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
2.誘導電動機の比例推移
誘導電動機のトルク\( \ T \ \)に対する変数は可変抵抗である二次抵抗\( \ r_{2}^{\prime } \ \)と滑り\( \ s \ \)のみであり,トルク\( \ T \ \)を一定とすると,
\[
\begin{eqnarray}
\frac {r_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
解答:(4)
ワンポイント解説「1.誘導電動機の二次回路の入力,出力,損失の関係」より,二次回路の損失\( \ P_{\mathrm {c2}} \ \)は二次抵抗に比例するため,本問においては二次抵抗は\( \ 30 \ \)倍となり,比例推移の関係より,滑りも\( \ 30 \ \)倍となる。
したがって,二次抵抗を大きくした際の滑り\( \ s_{2} \ \)は,二次抵抗を大きくする前の滑りを\( \ s_{1}=0.01 \ \)と置くと,
\[
\begin{eqnarray}
s_{2} &=& s_{1}\times 30 \\[ 5pt ]
&=& 0.3 \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.誘導電動機の二次回路の入力,出力,損失の関係」より,定格出力\( \ P_{\mathrm {o1}} \ \)と二次抵抗を大きくした後の出力\( \ P_{\mathrm {o2}} \ \)との関係は,
\[
\begin{eqnarray}
\frac {P_{\mathrm {o2}}}{P_{\mathrm {o1}}} &=& \frac {(1-s_{2})P_{2}}{(1-s_{1})P_{2}} \\[ 5pt ]
&=& \frac {1-s_{2}}{1-s_{1}} \\[ 5pt ]
&=& \frac {1-0.3}{1-0.01} \\[ 5pt ]
&≒& 0.707 → 70 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは