Contents
【問題】
【難易度】★★★★★(難しい)
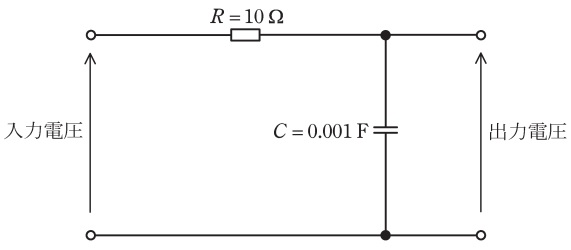
次の文章は,図に示す抵抗\( \ \mathrm {R} \ \),並びにキャパシタ\( \ \mathrm {C} \ \)で構成された一次遅れ要素に関する記述である。
図の回路において,入力電圧に対する出力電圧を,一次遅れ要素の周波数伝達関数として表したとき,折れ点角周波数\( \ \omega _{\mathrm {c}} \ \)は\( \ \fbox { (ア) } \ \mathrm {rad / s} \ \)である。ゲイン特性は,\( \ \omega _{\mathrm {c}} \ \)よりも十分低い角周波数ではほぼ一定の\( \ \fbox { (イ) } \ \mathrm {dB} \ \)であり,\( \ \omega _{\mathrm {c}} \ \)よりも十分高い角周波数では,角周波数が\( \ 10 \ \)倍になるごとに\( \ \fbox { (ウ) } \ \mathrm {dB} \ \)減少する直線となる。また,位相特性は, \( \ \omega _{\mathrm {c}} \ \)よりも十分高い角周波数でほぼ一定の\( \ \fbox { (エ) } \ ° \ \)の遅れとなる。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 100 & 20 & 10 & 45 \\
\hline
(2) & 100 & 0 & 20 & 90 \\
\hline
(3) & 100 & 0 & 20 & 45 \\
\hline
(4) & 0.01 & 0 & 10 & 90 \\
\hline
(5) & 0.01 & 20 & 20 & 45 \\
\hline
\end{array}
\]
【ワンポイント解説】
自動制御におけるゲインと位相の特性を求める問題です。
周波数伝達関数を求め,ゲインと位相の特性を求める計算量も多い問題で,令和3年度の試験の中でもかなり難易度が高い問題であったと思います。
少し時間がかかる問題なので,試験の際には一旦飛ばすことも検討しても良いかもしれません。
1.周波数伝達関数のゲイン
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)で与えられる時,この周波数伝達関数の絶対値\( \ \left| W(\mathrm {j}\omega ) \right| \ \)は,
\[
\begin{eqnarray}
\left| W(\mathrm {j}\omega ) \right| &=&\left| \frac {K}{1+\mathrm {j}\omega T}\right| \\[ 5pt ]
&=&\frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \\[ 5pt ]
&=&\frac {K}{\sqrt {1+\omega ^{2}T^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,この周波数伝達関数のゲイン\( \ g \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10} \frac {K}{\sqrt {1+\omega ^{2}T^{2}}} \\[ 5pt ]
&=&20\log _{10} K-20\log _{10} \sqrt {1+\omega ^{2}T^{2}} \\[ 5pt ]
&=&20\log _{10} K-10\log _{10} \left( 1+\omega ^{2}T^{2}\right) \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.ボード線図
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)で与えられる時,ゲイン\( \ g \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10} \frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
となりますが,\( \ \displaystyle \omega \ll \frac {1}{T} \ \)すなわち\( \ \omega T \ll 1 \ \)のとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {1+0}} \\[ 5pt ]
&=&20\log _{10}K \\[ 5pt ]
\end{eqnarray}
\]
とほぼ一定の値となり,\( \ \displaystyle \omega \gg \frac {1}{T} \ \)すなわち\( \ \omega T \gg 1 \ \)のとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {\left( \omega T\right) ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ]
&=&20\log _{10} K-20\log _{10}\omega T \\[ 5pt ]
\end{eqnarray}
\]
となり,横軸に対数座標をとると,ほぼ直線的に減少していくことになります。したがって,ボード線図は図1のようになります。
図1において\( \ \displaystyle \omega =\frac {1}{T} \ \)となる角周波数を折れ点角周波数と呼びます。

【解答】
解答:(2)
(ア)
入力電圧を\( \ v_{\mathrm {i}} \ \),出力電圧を\( \ v_{\mathrm {o}} \ \)とすると,分圧の法則より,
\[
\begin{eqnarray}
v_{\mathrm {o}}&=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}}{\displaystyle R+\frac {1}{\mathrm {j}\omega C}}v_{\mathrm {i}} \\[ 5pt ]
&=&\frac {1}{1+\mathrm {j}\omega CR}v_{\mathrm {i}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,周波数伝達関数\( \ \displaystyle W\left( \mathrm {j}\omega \right) =\frac {v_{\mathrm {o}}}{v_{\mathrm {i}}} \ \)は,
\[
\begin{eqnarray}
W\left( \mathrm {j}\omega \right) &=&\frac {1}{1+\mathrm {j}\omega CR} \\[ 5pt ]
&=&\frac {1}{1+\mathrm {j}\omega 0.001\times 10} \\[ 5pt ]
&=&\frac {1}{1+\mathrm {j}0.01\omega } \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.ボード線図」の通り,折れ点角周波数\( \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {c}} &=&\frac {1}{CR} \\[ 5pt ]
&=&\frac {1}{ 0.001\times 10} \\[ 5pt ]
&=&100 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(イ)
ゲイン\( \ g \ \mathrm {[dB]} \ \)は,ワンポイント解説「1.周波数伝達関数のゲイン」より,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10} \left| \frac {1}{1+\mathrm {j}0.01\omega }\right| \\[ 5pt ]
&=&20\log _{10} \frac {1}{\sqrt {1+\left( 0.01\omega \right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \omega \ \)が十分に小さいとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {1}{\sqrt {1+0}} \\[ 5pt ]
&=&20\log _{10} 1 \\[ 5pt ]
&=&0 \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(ウ)
\( \ \omega \ \)が十分に大きいときゲイン\( \ g \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10} \frac {1}{\sqrt {1+\left( 0.01\omega \right) ^{2}}} \\[ 5pt ]
&≃&20\log _{10} \frac {1}{\sqrt {\left( 0.01\omega \right) ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {1}{0.01\omega } \\[ 5pt ]
&=&-20\log _{10} \left( 0.01\omega \right) \\[ 5pt ]
&=&-20\log _{10} 0.01-20\log _{10} \omega \\[ 5pt ]
&=&40-20\log _{10} \omega \\[ 5pt ]
\end{eqnarray}
\]
となるので,角周波数が\( \ 10 \ \)倍になるごとに\( \ 20 \ \mathrm {[dB]} \ \)ずつ減少していくことがわかる。
(エ)
周波数伝達関数\( \ \displaystyle W\left( \mathrm {j}\omega \right) \ \)を整理すると,
\[
\begin{eqnarray}
W\left( \mathrm {j}\omega \right) &=&\frac {1}{1+\mathrm {j}0.01\omega } \\[ 5pt ]
&=&\frac {1}{1+\mathrm {j}0.01\omega }\times \frac {1-\mathrm {j}0.01\omega }{1-\mathrm {j}0.01\omega } \\[ 5pt ]
&=&\frac {1}{1+0.01^{2}\omega ^{2} }\left( 1-\mathrm {j}0.01\omega \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,位相\( \ \theta \ \)は,
\[
\begin{eqnarray}
\tan \theta &=&\frac {-0.01\omega }{1} \\[ 5pt ]
&=&-0.01\omega \\[ 5pt ]
\theta &=&\tan ^{-1}\left( -0.01\omega \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \omega \ \)が十分に大きいとき\( \ \tan \theta \ \)は\( \ -\infty \ \)へ近づいていくので,\( \ \theta \ \)は\( \ -90 \ ° \ \)すなわち\( \ 90 \ ° \ \)の遅れとなる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは