Contents
【問題】
【難易度】★★★★☆(やや難しい)
一般的な三相かご形誘導電動機がある。
出力が大きい定格運転条件では,誘導機の等価回路の電流は,「二次電流\(≫\)励磁電流」であるから,励磁回路を省略しても特性をほぼ表現できる。さらに,「二次抵抗による電圧降下\(≫\)その他の電圧降下」となるので,一次抵抗と漏れリアクタンスを省略しても,おおよその特性を検討できる。
このような電動機でトルク一定負荷の場合に,電流\(100 \ \mathrm {A}\)の定格運転から電源電圧と周波数を共に\(10 \ %\)下げて回転速度を少し下げた。このときの電動機の電流の値\(\mathrm {[A]}\)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 80 (2) 90 (3) 100 (4) 110 (5) 120
【ワンポイント解説】
誘導機の定トルク運転時の特性を知っていれば,計算いらずで答えを導き出すことができますが,解説ではトルクの導出から解を求めたいと思います。
1.誘導電動機の等価回路
誘導電動機の等価回路は図1のようになります。ここで\({\dot V}_{1}\)は一次電圧,\({\dot I}_{1}\)は一次電流,\({\dot I}_{0}\)は励磁電流,\({\dot I}_{2}\)は二次電流,\(r_{1}\)は一次巻線抵抗,\(r_{2}^{\prime }\)は二次抵抗の一次換算値,\(x_{1}\)は一次漏れリアクタンス,\(x_{2}^{\prime }\)は二次漏れリアクタンスの一次換算値,\(s\)は滑りとなります。
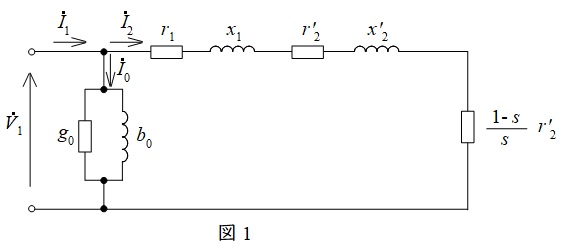
2.電動機の同期速度と同期角速度
極数\(p\)の電動機が周波数\(f\)の電源で運転されている時,同期速度\(n_{\mathrm {s}} \ \mathrm {[{min}^{-1}]}\)と同期角速度\(\omega _{\mathrm {s}} \ \mathrm {[rad/s]}\)は,
\[
\begin{eqnarray}
n_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\omega _{\mathrm {s}}&=&\frac {2\pi n_{\mathrm {s}}}{60} \\[ 5pt ]
&=&\frac {4\pi f}{p}\\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
解答:(3)
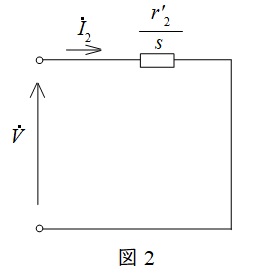
題意より,励磁回路及び一次抵抗と漏れリアクタンスは無視できるので,本問の誘導電動機の等価回路は図2のようになる。
図2において,
\[
I_{2}=\frac {V}{\displaystyle \frac {r_{2}}{s}}
\]
であり,二次入力\(P_{2}\)は,
\[
\begin{eqnarray}
P_{2} &=&\frac {3r_{2}I_{2}^{2}}{s} \\[ 5pt ]
\end{eqnarray}
\]
である。トルク\(T\)は,同期角速度\(\omega _{\mathrm {s}}\),出力\(P_{\mathrm {o}}\)の時の角速度\(\omega \)とすると,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {P_{2} (1-s)}{\omega _{\mathrm {s}} (1-s) } \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=&\frac {3r_{2}I_{2}^{2}}{s\omega _{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\(\displaystyle V=\frac {r_{2}}{s}I_{2}\)及びワンポイント解説「2.電動機の同期速度と同期角速度」より,
\[
\begin{eqnarray}
T &=&\frac {3VI_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=&\frac {3pVI_{2}}{4\pi f} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで電源電圧と周波数を\(10 \ %\)下げた時の電流を\(I_{2}^{\prime }\)とすると,トルクは変化ないので,
\[
\begin{eqnarray}
\frac {3pVI_{2}}{4\pi f} &=&\frac {3p\cdot 0.9VI_{2}^{\prime}}{4\pi \cdot 0.9f} \\[ 5pt ]
I_{2}&=&I_{2}^{\prime} \\[ 5pt ]
\end{eqnarray}
\]
となり,電流の値は変化しない(\(100 \ \mathrm {A}\))ことが分かる。





















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは