《機械》〈回転機〉[R2:問15]三相誘導電動機の二次入力（同期ワット）と滑りの特性に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

定格出力\( \ 45 \ \mathrm {kW} \ \)，定格周波数\( \ 60 \ \mathrm {Hz} \ \)，極数\( \ 4 \ \)，定格運転時の滑りが\( \ 0.02 \ \)である三相誘導電動機について，次の(a)及び(b)の問に答えよ。

(a)　この誘導電動機の定格運転時の二次入力（同期ワット）の値\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 43 \ \)　　(2)　\( \ 44 \ \)　　(3)　\( \ 45 \ \)　　(4)　\( \ 46 \ \)　　(5)　\( \ 47 \ \)

(b)　この誘導電動機を，電源周波数\( \ 50 \ \mathrm {Hz} \ \)において，\( \ 60 \ \mathrm {Hz} \ \)運転時の定格出力トルクと同じ出力トルクで連続して運転する。この\( \ 50 \ \mathrm {Hz} \ \)での運転において，滑りが\( \ 50 \ \mathrm {Hz} \ \)を基準として\( \ 0.05 \ \)であるときの誘導電動機の出力の値\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 36 \ \)　　(2)　\( \ 38\ \)　　(3)　\( \ 45 \ \)　　(4)　\( \ 54 \ \)　　(5)　\( \ 56 \ \)

【ワンポイント解説】

(a)は基本問題ですが，(b)は誘導電動機の特性をしっかりと理解していないと解けない問題です。
こういう問題では(a)を確実に得点しておくことが重要となります。
本問はどちらかというと，等価回路を描いて解く問題ではないかもしれませんが，誘導電動機の基本となる等価回路は確実に描けるようにしておきましょう。

1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

2.三相誘導電動機の回転数\( \ N \ \)と角速度\( \ \omega \ \)の関係
三相誘導電動機の回転数\( \ N \ \mathrm {[{min}^{-1}]} \ \)とすると，角速度\( \ \omega \ \mathrm {[rad/s]} \ \)は，
\[
\begin{eqnarray}
\omega &=&\frac {2\pi N}{60} \\[ 5pt ] \end{eqnarray}
\] となります。

3.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \)，回転数が\( \ N \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となり，上式を変形すると，
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ] N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ] &=&N_{\mathrm {s}}\left( 1-s\right) \\[ 5pt ] \end{eqnarray}
\] となります。

4.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
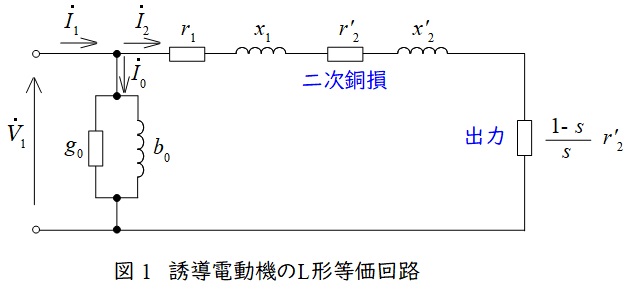
誘導電動機のL形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2} \ \)は二次電流，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。
図1より，出力\( \ P_{\mathrm {o}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)，二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& \frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機の二次入力\( \ P_{2} \ \)，出力\( \ P_{\mathrm {o}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

5.出力\( \ P_{\mathrm {o}} \ \)とトルク\( \ T \ \)の関係
誘導電動機の出力\( \ P_{\mathrm {o}} \ \)とトルク\( \ T \ \)には，角速度を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
T &=& \frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(a)解答：(4)
ワンポイント解説「4.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」より，誘導電動機の二次入力\( \ P_{2} \ \)，出力\( \ P_{\mathrm {o}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があるので，
\[
\begin{eqnarray}
P_{2} &=&\frac {P_{\mathrm {o}}}{1-s} \\[ 5pt ] &=&\frac {45}{1-0.02} \\[ 5pt ] &≒&45.9 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
電源周波数\( \ 50 \ \mathrm {Hz} \ \)の時も\( \ 60 \ \mathrm {Hz} \ \)の時も，同じ出力トルクで運転しているので，ワンポイント解説「5.二次入力\( \ P_{2} \ \)及び出力\( \ P_{\mathrm {o}} \ \)とトルク\( \ T \ \)の関係」より，
\[
\begin{eqnarray}
T = \frac {P_{\mathrm {o50}}}{\omega _{\mathrm {50}}}&=& \frac {P_{\mathrm {o60}}}{\omega _{\mathrm {60}}} \\[ 5pt ] \frac {P_{\mathrm {o50}}}{\displaystyle \frac {2\pi N _{\mathrm {50}}}{60}}&=& \frac {P_{\mathrm {o60}}}{\displaystyle \frac {2\pi N _{\mathrm {60}}}{60}} \\[ 5pt ] \frac {P_{\mathrm {o50}}}{N _{\mathrm {50}}}&=& \frac {P_{\mathrm {o60}}}{N _{\mathrm {60}}} \\[ 5pt ] P_{\mathrm {o50}}&=& \frac {N _{\mathrm {50}}}{N _{\mathrm {60}}}P_{\mathrm {o60}}　・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。ここで，ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)」及び「3.誘導機の滑り\( \ s \ \)」より，\( \ 50 \ \mathrm {Hz} \ \)及び\( \ 60 \ \mathrm {Hz} \ \)の回転数\( \ N_{\mathrm {50}} \ \mathrm {[{min}^{-1}]} \ \)及び\( \ N_{\mathrm {60}} \ \mathrm {[{min}^{-1}]} \ \)を求めると，
\[
\begin{eqnarray}
N_{\mathrm {50}} &=&\frac {120\times f_{50}}{p}\times \left( 1-s_{50} \right) \\[ 5pt ] &=&\frac {120\times 50}{4}\times \left( 1-0.05 \right) \\[ 5pt ] &=&1425 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] N_{\mathrm {60}} &=&\frac {120\times f_{60}}{p}\times \left( 1-s_{60} \right) \\[ 5pt ] &=&\frac {120\times 60}{4}\times \left( 1-0.02 \right) \\[ 5pt ] &=&1764 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] であるから，これを①に代入すると，
\[
\begin{eqnarray}
P_{\mathrm {o50}}&=& \frac {1425}{1764}\times 45 \\[ 5pt ] &≒& 36.4 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。