《機械》〈回転機〉[R4上:問2]三相誘導電動機の拘束試験結果からの始動電流の特定に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

\( \ \Delta \ \)結線された三相誘導電動機がある。この電動機に対し，\( \ \Delta \ \)結線の状態で拘束試験を実施したところ，下表の結果が得られた。この電動機を\( \ \mathrm {Y} \ \)結線に切り替え，\( \ 220 \ \mathrm {V} \ \)の三相交流電源に接続して始動するときの始動電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，磁気飽和による漏れリアクタンスの低下は無視できるものとする。

\[
\begin{array}{|l|c|}
\hline
　一次電圧（線間電圧）　　　& 　　43.0 \ \mathrm {V}　　 \\
\hline
　一次電流（線電流）　　& 　　9.00 \ \mathrm {A}　　 \\
\hline
\end{array}
\]

　(1)　\( \ 15.3 \ \)　　(2)　\( \ 26.6 \ \)　　(3)　\( \ 46.0 \ \)　　(4)　\( \ 79.8 \ \)　　(5)　\( \ 138 \ \)

【ワンポイント解説】

三相交流の\( \ \mathrm {Y} \ \)結線と\( \ \Delta \ \)結線の特徴を理解しているかを問う問題です。
機械科目というよりは理論科目に近い内容の問題ですが，それぞれの相電圧と線間電圧，相電流と線電流の関係はしっかりと理解しておくようにしましょう。
以下の説明は電源側の内容ですが，負荷側でも同様に考えれば大丈夫です。

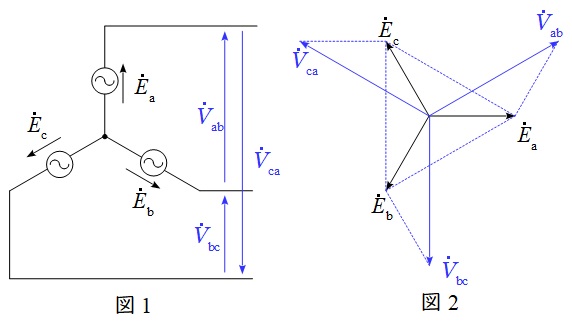
1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
図1のような三相対称電源がある時，線間電圧と相電圧の関係は図2のベクトル図のようになり，線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると，
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ] V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ] V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)進みであることが分かります。

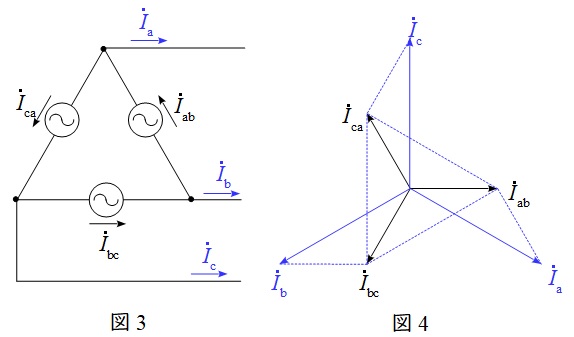
2.\( \ \Delta \ \)結線における相電流と線電流の関係
図3のような三相対称電源がある時，線電流と相電流の関係は図4のベクトル図のようになり，線電流の大きさは相電流の大きさと比較すると，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ] I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ] I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)遅れであることが分かります。

【解答】

解答：(1)
ワンポイント解説「2.\( \ \Delta \ \)結線における相電流と線電流の関係」の通り，\( \ \Delta \ \)結線においては線間電圧の大きさと相電圧の大きさが等しく，線電流の大きさが相電流の大きさの\( \ \sqrt {3} \ \)倍であるので，拘束試験時の各相の電圧\( \ E_{\mathrm {t}} \ \mathrm {[V]} \ \)及び電流\( \ I_{\mathrm {t}} \ \mathrm {[A]} \ \)の大きさは，
\[
\begin{eqnarray}
E_{\mathrm {t}} &=&43.0 \ \mathrm {[V]} \\[ 5pt ] I_{\mathrm {t}} &=&\frac {9.00}{\sqrt {3}} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。また，ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り，\( \ \mathrm {Y} \ \)結線においては線間電圧の大きさが相電圧の\( \ \sqrt {3} \ \)倍であるため，始動時の各相の電圧\( \ E_{\mathrm {s}} \ \mathrm {[V]} \ \)の大きさは，
\[
\begin{eqnarray}
E_{\mathrm {s}} &=&\frac {220}{\sqrt {3}} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。拘束試験時と始動時の電圧電流が比例するため，始動時の相電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {s}} &=&\frac {E_{\mathrm {s}}}{E_{\mathrm {t}}}I_{\mathrm {t}} \\[ 5pt ] &=&\frac {\displaystyle \frac {220}{\sqrt {3}}}{43}\times \frac {9.00}{\sqrt {3}} \\[ 5pt ] &≒&15.3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り，\( \ \mathrm {Y} \ \)結線においては線電流の大きさと相電流の大きさが等しいことから，始動電流の大きさは\( \ 15.3 \ \mathrm {[A]} \ \)と求められる。