《機械》〈変圧器〉[R05下:問8]変圧器の各諸量の二次側換算に関する論説問題

【問題】

【難易度】★★★☆☆（普通）

変圧器の一次側（巻数\( \ N_{1} \ \)）の諸量を二次側（巻数\( \ N_{2} \ \)）に換算した場合の簡易等価回路の換算係数に関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。ただし，この変圧器の巻数比\( \ \left( \displaystyle \frac {N_{1}}{N_{2}} \right) \ \)を\( \ a \ \)とする。

(1) 一次側の電圧は\( \ \displaystyle \frac {1}{a} \ \)倍

(2) 一次側の電流は\( \ a \ \)倍

(3) 励磁電流は\( \ a \ \)倍

(4) 一次側のインピーダンスは\( \ \displaystyle \frac {1}{a^{2}} \ \)倍

(5) 励磁アドミタンスは\( \ \displaystyle \frac {1}{a^{2}} \ \)倍

【ワンポイント解説】

変圧器の電圧・電流・インピーダンス・アドミタンスの二次側換算に関する問題です。
\( \ \mathrm {L} \ \)形簡易等価回路では一次側換算することが多いですが，本問は二次側換算となっています。二次側換算する場合は励磁回路は一次回路と同様に扱います。
本問は平成9年問3からの再出題となります。

1.変圧器の巻数比と変圧比，変流比，インピーダンス比の関係
変圧器の一次側の巻数\( \ N_{1} \ \)，電圧\( \ V_{1} \ \mathrm {[V]} \ \)，電流\( \ I_{1} \ \mathrm {[A]} \ \)，二次側の巻数\( \ N_{2} \ \)，電圧\( \ V_{2} \ \mathrm {[V]} \ \)，電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると，巻数比\( \ \displaystyle a=\frac {N_{1}}{N_{2}} \ \)は，
\[
\begin{eqnarray}
a&=&\frac {N_{1}}{N_{2}} =\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。\( \ \displaystyle \frac {V_{1}}{V_{2}} \ \)を変圧比，\( \ \displaystyle \frac {I_{1}}{I_{2}} \ \)を変流比といいます。
また，一次側のインピーダンスを\( \ Z_{1} \ \mathrm {[\Omega ]} \ \)，二次側のインピーダンスを\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると，インピーダンス比\( \ \displaystyle \frac {Z_{1}}{Z_{2}} \ \)は，
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}}&=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {V_{1}}{V_{2}}}{\displaystyle \frac {I_{1}}{I_{2}}} \\[ 5pt ] &=&\frac {a}{\displaystyle \frac {1}{a}} \\[ 5pt ] &=&a^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

2.変圧器の等価回路（一次換算）と鉄損及び銅損
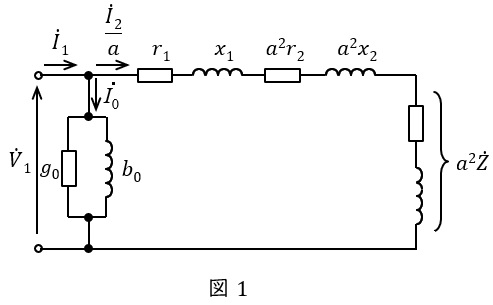
変圧器の一次側換算簡易等価回路を図1に示します。ただし，\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流，\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は二次電流，\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流，\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗，\( \ r_{2} \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗，\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス，\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンス，\( \ g_{0} \ \mathrm {[S]} \ \)は励磁コンダクタンス，\( \ b_{0} \ \mathrm {[S]} \ \)は励磁サセプタンス，\( \ a \ \)は変圧比（巻数比）となります。
等価回路より，鉄損（\( \ g_{0} \ \mathrm {[S]} \ \)での損失）は電圧\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)の\( \ 2 \ \)乗に比例し，銅損（\( \ r_{1} \ \mathrm {[\Omega ]} \ \)，\( \ r_{2} \ \mathrm {[\Omega ]} \ \)での損失の合計）は電流\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)の\( \ 2 \ \)乗に比例することがわかります。

【解答】

解答：(5)
(1)正しい
ワンポイント解説「1.変圧器の巻数比と変圧比，変流比，インピーダンス比の関係」の通り，二次側に換算した場合，一次側の電圧は\( \ \displaystyle \frac {1}{a} \ \)倍となります。

(2)正しい
ワンポイント解説「1.変圧器の巻数比と変圧比，変流比，インピーダンス比の関係」の通り，二次側に換算した場合，一次側の電流は\( \ a \ \)倍となります。

(3)正しい
ワンポイント解説「1.変圧器の巻数比と変圧比，変流比，インピーダンス比の関係」の通り，二次側に換算した場合，励磁電流は\( \ a \ \)倍となります。

(4)正しい
ワンポイント解説「1.変圧器の巻数比と変圧比，変流比，インピーダンス比の関係」の通り，二次側に換算した場合，一次側のインピーダンスは\( \ \displaystyle \frac {1}{a^{2}} \ \)倍

(5)誤り
ワンポイント解説「1.変圧器の巻数比と変圧比，変流比，インピーダンス比の関係」の通り，励磁アドミタンス\( \ Y_{0} \ \mathrm {[S]} \ \)を二次側換算した\( \ {Y_{0}}^{\prime } \ \mathrm {[S]} \ \)は，
\[
\begin{eqnarray}
{Y_{0}}^{\prime }&=&\frac {{I_{0}}^{\prime }}{{V_{0}}^{\prime }} \\[ 5pt ] &=&\frac {\displaystyle aI_{0}}{\displaystyle \frac {V_{0}}{a}} \\[ 5pt ] &=&a^{2}\frac {I_{0}}{V_{0}} \\[ 5pt ] &=&a^{2}Y_{0} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ a^{2} \ \)倍となります。