《機械》〈直流機〉[R06下:問2]直流電動機の電機子巻線の抵抗値に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

界磁磁束を一定に保った直流電動機が，電機子電圧\( \ 24 \ \mathrm {V} \ \)，電機子電流\( \ 3.0 \ \mathrm {A} \ \)で一定速で駆動されている。このときの直流電動機の回転数は\( \ 1 \ 500 \ \mathrm {{min}^{-1}} \ \)，出力トルクは\( \ 0.4 \ \mathrm {N\cdot m} \ \)であった。この直流電動機の電機子巻線の抵抗値\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，ブラシによる電圧降下，及び電機子反作用は無視できるものとし，考慮すべき損失は電機子巻線の銅損のみとする。

　(1)　\( \ 1.0 \ \)　　(2)　\( \ 2.3 \ \)　　(3)　\( \ 3.1 \ \)　　(4)　\( \ 4.5 \ \)　　(5)　\( \ 6.9 \ \)

【ワンポイント解説】

与えられたパラメータを基に直流電動機の電機子巻線抵抗値を求める問題です。
様々な知識を活用して解く問題なので，慣れるまでは厳しい問題ですが，毎回のように直流電動機の計算問題は出題されているので，慣れてしまえば十分に得点源になり得る問題です。
総じて受験生の正答率が低い問題なので，各等価回路や公式をマスターしてライバルとの差を拡げるようにして下さい。

1.直流他励電動機の等価回路と特性
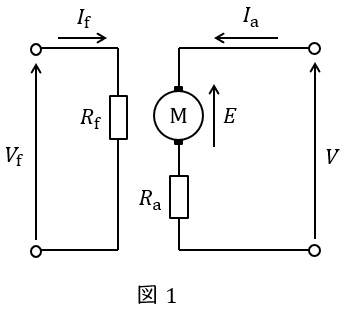
直流他励電動機の等価回路を図1に示します。ただし，図において，\( \ E \ \mathrm {[V]} \ \)は誘導起電力（逆起電力），\( \ V \ \mathrm {[V]} \ \)は端子電圧，\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \mathrm {[A]} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \mathrm {[\Omega ]} \ \)は界磁抵抗です。
等価回路より，回路方程式は，
\[
\begin{eqnarray}
V &=&E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となります。
また，磁束を\( \ \phi \ \mathrm {[Wb]} \ \)，回転速度を\( \ N \ \mathrm {[{min}^{-1}]} \ \)とすると，\( \ \phi ∝ I_{\mathrm {f}} \ \)となるので，誘導起電力(逆起電力)\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}^{\prime } I_{\mathrm {f}} N \\[ 5pt ] \end{eqnarray}
\] となり，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となります。このときの電動機の出力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&EI_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.直流電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係
直流電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係は，角速度\( \ \omega \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
P &=&\omega T \\[ 5pt ] \end{eqnarray}
\] の関係があり，このときの回転速度が\( \ N \ \mathrm {[min^{-1}]} \ \)であるとき，\( \ \displaystyle \omega =\frac {2\pi N}{60} \ \)の関係より，
\[
\begin{eqnarray}
P &=&\frac {2\pi N}{60} T \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
電動機の回転速度が\( \ N=1 \ 500 \ \mathrm {[{min}^{-1}]} \ \)より角速度\( \ \omega \ \mathrm {[rad / s]} \ \)は，ワンポイント解説「2.直流電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係」の通り，
\[
\begin{eqnarray}
\omega &=&\frac {2\pi N}{60} \\[ 5pt ] &=&\frac {2\pi \times 1 \ 500}{60} \\[ 5pt ] &≒&157.1 \ \mathrm {[rad / s]} \\[ 5pt ] \end{eqnarray}
\] となるので，トルク\( \ T=0.4 \ \mathrm {[N\cdot m]} \ \)より出力\( \ P \ \mathrm {[W]} \ \)は，ワンポイント解説「2.直流電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係」の通り，
\[
\begin{eqnarray}
P &=&\omega T \\[ 5pt ] &=&157.1\times 0.4 \\[ 5pt ] &=&62.84 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，電機子電流\( \ I_{\mathrm {a}}=3.0 \ \mathrm {[A]} \ \)より，電動機の誘導起電力\( \ E \ \mathrm {[V]} \ \)は，ワンポイント解説「1.直流他励電動機の等価回路と特性」の通り，
\[
\begin{eqnarray}
E &=&\frac {P}{I_{\mathrm {a}}} \\[ 5pt ] &=&\frac {62.84}{3.0} \\[ 5pt ] &≒&20.95 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，電機子電圧\( \ V=24 \ \mathrm {[V]} \ \)より電機子巻線の抵抗値\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「1.直流他励電動機の等価回路と特性」の通り，
\[
\begin{eqnarray}
V &=&E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] R_{\mathrm {a}}I_{\mathrm {a}} &=&V-E \\[ 5pt ] R_{\mathrm {a}} &=&\frac {V-E}{I_{\mathrm {a}}} \\[ 5pt ] &=&\frac {24-20.95}{3} \\[ 5pt ] &≒&1.02 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。