《理論》〈電気回路〉[H18:問6]既知の抵抗と電流値からの未知の抵抗の抵抗値の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

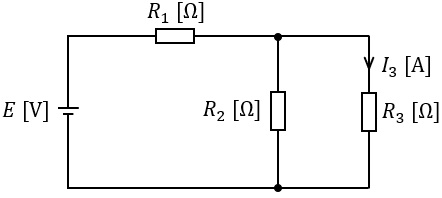
図のように，既知の直流電源\( \ E \ \mathrm {[V]} \ \)，未知の抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)，既知の抵抗\( \ R_{2} \ \mathrm {[\Omega ]} \ \)及び\( \ R_{3} \ \mathrm {[\Omega ]} \ \)からなる直流回路がある。抵抗\( \ R_{3} \ \mathrm {[\Omega ]} \ \)に流れる電流が\( \ I_{3} \ \mathrm {[A]} \ \)であるとき，抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)を求める式として，正しいのは次のうちどれか。

　(1)　\( \ \displaystyle R_{1}=\frac {R_{2}R_{3}}{R_{2}+R_{3}}\left( \frac {E}{R_{2}I_{3}}-\frac {R_{2}}{R_{3}}\right) \ \)

　(2)　\( \ \displaystyle R_{1}=\frac {R_{2}R_{3}}{R_{2}+R_{3}}\left( \frac {E}{R_{2}I_{3}}-\frac {R_{3}}{R_{2}}\right) \ \)

　(3)　\( \ \displaystyle R_{1}=\frac {R_{2}R_{3}}{R_{2}+R_{3}}\left( \frac {E}{R_{2}I_{3}}-1\right) \ \)

　(4)　\( \ \displaystyle R_{1}=\frac {R_{2}R_{3}}{R_{2}+R_{3}}\left( \frac {E}{R_{3}I_{3}}-\frac {R_{3}}{R_{2}}\right) \ \)

　(5)　\( \ \displaystyle R_{1}=\frac {R_{2}R_{3}}{R_{2}+R_{3}}\left( \frac {E}{R_{3}I_{3}}-1\right) \ \)

【ワンポイント解説】

既知の抵抗と電流値から，未知の抵抗の抵抗値を求める問題です。
いわゆる一般の電気回路の問題のように求められる値を順番に求める問題ではなく，未知の\( \ R_{1} \ \mathrm {[\Omega ]} \ \)を用いて，既知の\( \ I_{3} \ \mathrm {[A]} \ \)を求めて計算していく必要があるので，慣れていない方には厳しい問題であったかと思います。問題慣れの要素がありますので，本問で解法を理解するようにして下さい。

1.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.分圧・分流の法則
①分圧の法則
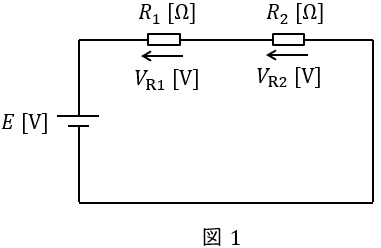
図1に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

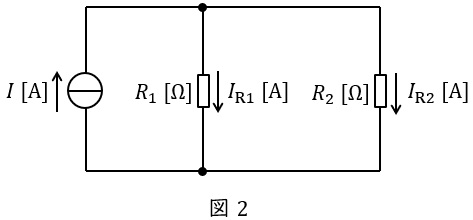
②分流の法則
図2に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(5)
回路全体の合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R&=&R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] \end{eqnarray}
\] となるので，電源\( \ E \ \mathrm {[V]} \ \)を流れる電流\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I&=&\frac {E}{R} \\[ 5pt ] &=&\frac {E}{\displaystyle R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}}} \\[ 5pt ] \end{eqnarray}
\] となる。これより，\( \ R_{3} \ \mathrm {[\Omega ]} \ \)に流れる電流\( \ I_{3} \ \mathrm {[A]} \ \)は，ワンポイント解説「2.分圧・分流の法則」の通り，
\[
\begin{eqnarray}
I_{3}&=&\frac {R_{2}}{R_{2}+R_{3}}I \\[ 5pt ] &=&\frac {R_{2}}{R_{2}+R_{3}}\cdot \frac {E}{\displaystyle R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}}} \\[ 5pt ] \end{eqnarray}
\] となるので，これを\( \ R_{1} \ \)について整理すると，
\[
\begin{eqnarray}
R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}}&=&\frac {R_{2}}{R_{2}+R_{3}}\cdot \frac {E}{I_{3}} \\[ 5pt ] R_{1}&=&\frac {R_{2}}{R_{2}+R_{3}}\cdot \frac {E}{I_{3}}-\frac {R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] &=&\frac {R_{2}R_{3}}{R_{2}+R_{3}}\left( \frac {E}{R_{3}I_{3}}-1\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。