【問題】
【難易度】★★★★☆(やや難しい)
図のように,直流電源にスイッチ\( \ \mathrm {S} \ \),抵抗\( \ 5 \ \)個を接続したブリッジ回路がある。この回路において,スイッチ\( \ \mathrm {S} \ \)を開いたとき,\( \ \mathrm {S} \ \)の両端間の電圧は\( \ 1 \ \mathrm {V} \ \)であった。スイッチ\( \ \mathrm {S} \ \)を閉じたときに\( \ 8 \ \mathrm {\Omega } \ \)の抵抗に流れる電流\( \ I \ \)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。

(1) \( \ 0.10 \ \) (2) \( \ 0.75 \ \) (3) \( \ 1.0 \ \) (4) \( \ 1.4 \ \) (5) \( \ 2.0 \ \)
【ワンポイント解説】
ブリッジ回路が変形してあると,急に理解できなくなる受験生が多くいらっしゃいます。まずは見慣れている回路に書き換え,丁寧に解くようにしましょう。また,ブリッジ回路はパターン化されている問題が多いので,問題に慣れてくると確実に得点できる分野に変わります。
1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時,それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。
①直列
直列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.テブナンの定理
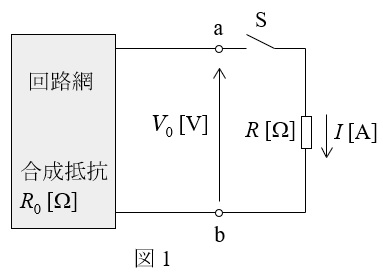
下図のような回路において,端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \),端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする(ただし,電圧源は短絡,電流源は開放する)と,図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【関連する「電気の神髄」記事】
【解答】
解答:(1)
問題図を書き換えると図2のようになる。
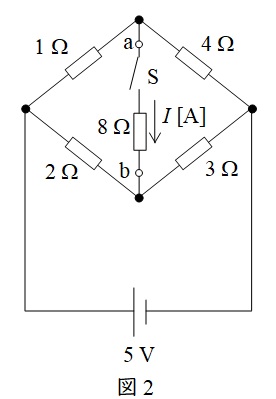
図2より,端子\( \ \mathrm {a} \ \)の開放電圧\( \ V_{\mathrm {a}} \ \mathrm {[V]} \ \)及び端子\( \ \mathrm {b} \ \)の開放電圧\( \ V_{\mathrm {b}} \ \mathrm {[V]} \ \)は,分圧の法則から,
\[
\begin{eqnarray}
V_{\mathrm {a}}&=&\frac {4}{1+4}\times 5 \\[ 5pt ]
&=&4 \ \mathrm {[V]} \\[ 5pt ]
V_{\mathrm {b}}&=&\frac {3}{2+3}\times 5 \\[ 5pt ]
&=&3 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {0}}&=&V_{\mathrm {a}}-V_{\mathrm {b}} \\[ 5pt ]
&=&4-3 \\[ 5pt ]
&=&1 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
で問題文と一致する。
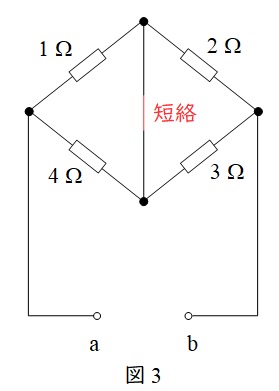
電圧源を短絡し,端子\( \ \mathrm {a-b} \ \)から電源側を見た回路は図3のように書き換えられるので,端子\( \ \mathrm {a-b} \ \)から電源側を見た合成抵抗\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {0}}&=&\frac {1\times 4}{1+4}+\frac {2\times 3}{2+3} \\[ 5pt ]
&=&0.8+1.2 \\[ 5pt ]
&=&2 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,ワンポイント解説「2.テブナンの定理」より,\( \ 8 \ \mathrm {\Omega } \ \)の抵抗に流れる電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ]
&=&\frac {1}{8+2} \\[ 5pt ]
&=&0.10 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは