《理論》〈電磁気〉[H19:問1]直線状導体と円形コイルが作る磁界の比較に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

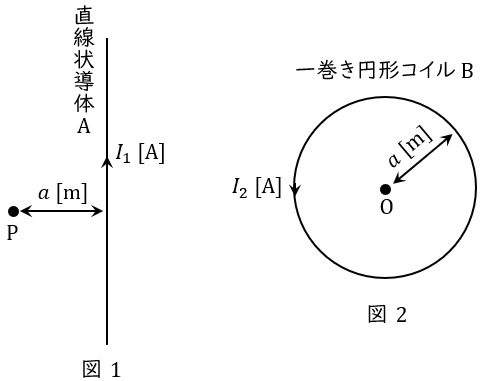
図1のように，無限に長い直線状導体\( \ \mathrm {A} \ \)に直流電流\( \ I_{1} \ \mathrm {[A]} \ \)が流れているとき，この導体から\( \ a \ \mathrm {[m]} \ \)離れた点\( \ \mathrm {P} \ \)での磁界の大きさは\( \ H_{1} \ \mathrm {[A / m]} \ \)であった。一方，図2のように半径\( \ a \ \mathrm {[m]} \ \)の一巻きの円形コイル\( \ \mathrm {B} \ \)に直流電流\( \ I_{2} \ \mathrm {[A]} \ \)が流れているとき，この円の中心点\( \ \mathrm {O} \ \)での磁界の大きさは\( \ H_{2} \ \mathrm {[A / m]} \ \)であった。\( \ H_{1}=H_{2} \ \)であるときの\( \ I_{1} \ \)と\( \ I_{2} \ \)の関係を表す式として，正しいのは次のうちどれか。

　(1)　\( \ I_{1}=\pi ^{2} I_{2} \ \)　　(2)　\( \ I_{1}=\pi I_{2} \ \)　　(3)　\( \ \displaystyle I_{1}=\frac {I_{2}}{\pi } \ \)　
　(4)　\( \ \displaystyle I_{1}=\frac {I_{2}}{\pi ^{2}} \ \)　　(5)　\( \ \displaystyle I_{1}=\frac {2}{\pi }I_{2} \ \)

【ワンポイント解説】

直線状導体と円形コイルが作る磁界の比較に関する問題です。
どちらの公式も法則ですから基本的には覚えるしかありません。いずれも電磁気においては非常に重要な公式となりますので，必ず覚えておくようにして下さい。

1.アンペアの周回積分の法則
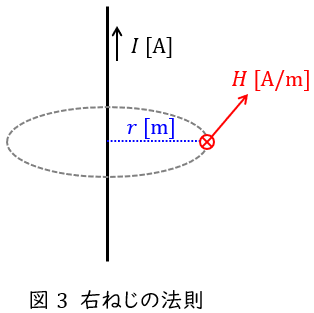
図3に示すように，電流\( \ I \ \mathrm {[A]} \ \)の流れる向きに右ねじを合わせる（図3においては上向き）と，右ねじを回す向きに磁界\( \ H \ \mathrm {[A / m ]} \ \)が発生し，距離\( \ r \ \mathrm {[m]} \ \)離れた場所の磁界の大きさは，
\[
\begin{eqnarray}
H &=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.ビオ・サバールの法則
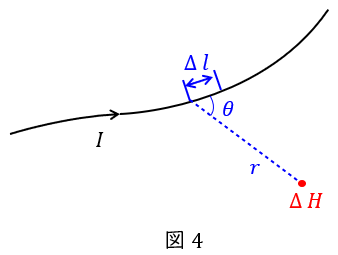
図4に示すように，微小な長さ\( \ \Delta l \ \mathrm {[m]} \ \)に流れる電流\( \ I \ \mathrm {[A]} \ \)が，距離\( \ r \ \mathrm {[m]} \ \)離れた場所に作る磁界\( \ \Delta H \ \mathrm {[A / m]} \ \)は，
\[
\begin{eqnarray}
\Delta H&=&\frac {I \Delta l}{4\pi r^{2}}\sin \theta \\[ 5pt ] \end{eqnarray}
\] となります。

3.円形コイルが中心点に作る磁界の大きさ
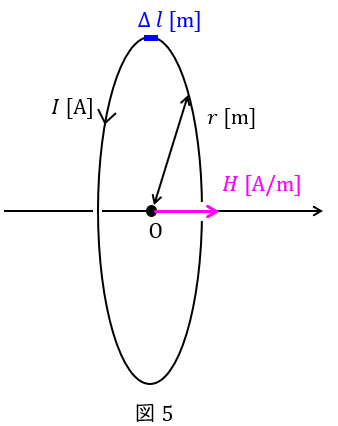
ビオ・サバールの法則を図5のような円形コイルに適用すると，コイルの長さが\( \ 2 \pi r \ \)であり，中心点\( \ \mathrm {O} \ \)から見た微小電流の角度\( \ \theta \ \)は常に\( \ 90° \ \)であるから，
\[
\begin{eqnarray}
H&=&\frac {I \times 2\pi r}{4\pi r^{2}}\sin 90° \\[ 5pt ] &=&\frac {I}{2r} \\[ 5pt ] \end{eqnarray}
\] となります。（この結果は公式として覚えておきましょう。）

【解答】

解答：(2)
図1における点\( \ \mathrm {P} \ \)での磁界の大きさ\( \ H_{1} \ \mathrm {[A / m]} \ \)は，ワンポイント解説「1.アンペアの周回積分の法則」の通り，
\[
\begin{eqnarray}
H_{1} &=&\frac {I_{1}}{2\pi a} \\[ 5pt ] \end{eqnarray}
\] となり，図2における中心点\( \ \mathrm {O} \ \)での磁界の大きさ\( \ H_{2} \ \mathrm {[A / m]} \ \)は，ワンポイント解説「3.円形コイルが中心点に作る磁界の大きさ」の通り，
\[
\begin{eqnarray}
H_{2}&=&\frac {I_{2}}{2a} \\[ 5pt ] \end{eqnarray}
\] となる。題意より，\( \ H_{1}=H_{2} \ \)であるため，
\[
\begin{eqnarray}
\frac {I_{1}}{2\pi a} &=&\frac {I_{2}}{2a} \\[ 5pt ] \frac {I_{1}}{\pi } &=&I_{2} \\[ 5pt ] I_{1}&=&\pi I_{2} \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかる。