《理論》〈電気回路〉[H25:問9]RLC並列回路の電圧電流波形に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

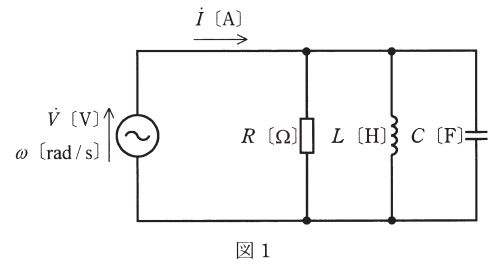
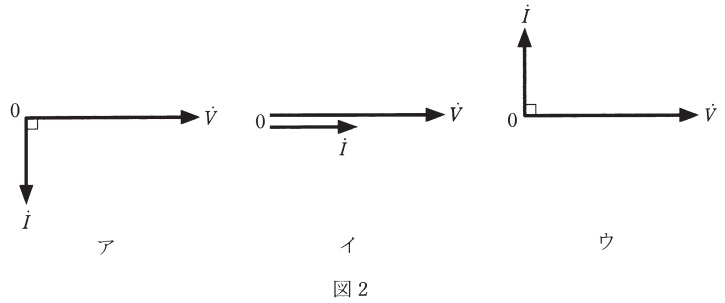
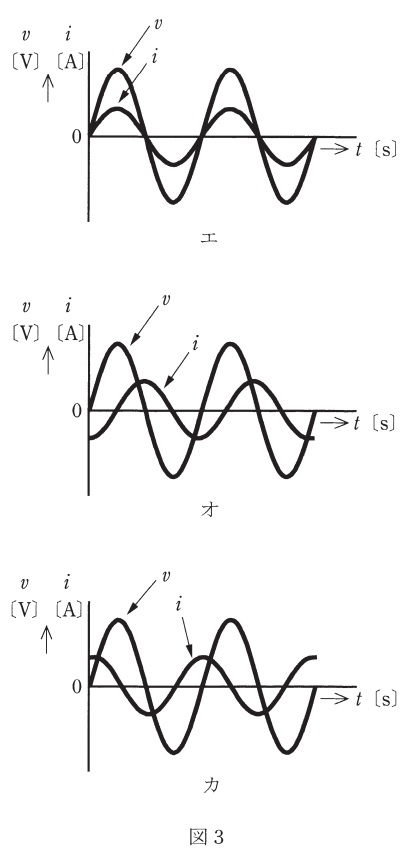
図1のように，\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗，インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル，静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサからなる並列回路がある。この回路に角周波数\( \ \omega \ \mathrm {[rad/s]} \ \)の交流電圧\( \ v \ \mathrm {[V]} \ \)を加えたところ，この回路に流れる電流は\( \ i \ \mathrm {[A]} \ \)であった。電圧\( \ v \ \mathrm {[V]} \ \)及び電流\( \ i \ \mathrm {[A]} \ \)のベクトルをそれぞれ電圧\( \ \dot V \ \mathrm {[V]} \ \)と電流\( \ \dot I \ \mathrm {[A]} \ \)とした場合，両ベクトルの関係を示す図2(ア，イ，ウ)及び\( \ v \ \mathrm {[V]} \ \)と\( \ i \ \mathrm {[A]} \ \)の時間\( \ t \ \mathrm {[s]} \ \)の経過による変化を示す図3(エ，オ，カ)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，\( \ R≫\omega L \ \)及び\( \ \displaystyle \omega L=\frac {2}{\omega C} \ \)とし，一切の過渡現象は無視するものとする。

\[
\begin{array}{ccc}
& 図2 & 図3 \\[ 5pt ] \hline
(1)　　 & 　　ア　　 & 　　オ　　 \\[ 5pt ] \hline
(2)　　 & 　　ア　　 & 　　カ　　 \\[ 5pt ] \hline
(3)　　 & 　　イ　　 & 　　エ　　 \\[ 5pt ] \hline
(4)　　 & 　　ウ　　 & 　　オ　　 \\[ 5pt ] \hline
(5)　　 & 　　ウ　　 & 　　カ　　 \\[ 5pt ] \hline \\[ 5pt ] \end{array}
\]

【ワンポイント解説】

本問の注意点としては，\( \ R≫\omega L \ \)なので，電流を流れやすいのは\( \ \omega L \ \)側であり，無視できるのは抵抗に流れる電流分となります。解答は定量的に求めていますが，試験では定性的に求める方が早くなりますので，できるだけどこの電流が一番多く流れ，全体として電流と電圧の関係がどうなるかがわかると理想です。

1.コイルやコンデンサのリアクタンス
インダクタンスが\( \ L \ \mathrm {[H]} \ \)のコイル及び静電容量が\( \ C \ \mathrm {[F]} \ \)のコンデンサを周波数\( \ f \ \mathrm {[Hz]} \ \)の交流電源に接続した時のそれぞれのリアクタンスの大きさ\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] &=&\mathrm {j}2\pi f L \\[ 5pt ] -\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
ワンポイント解説「1.コイルやコンデンサのリアクタンス」より抵抗，コイル，コンデンサに流れる電流\( \ {\dot I}_{\mathrm {R}} \ \)，\( \ {\dot I}_{\mathrm {L}} \ \)，\( \ {\dot I}_{\mathrm {C}} \ \)は，電源電圧\( \ \dot V \ \)を基準とすると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {R}}&=&\frac {V}{R} \\[ 5pt ] {\dot I}_{\mathrm {L}}&=&\frac {V}{\mathrm {j}\omega L} \\[ 5pt ] {\dot I}_{\mathrm {C}}&=&\mathrm {j}\omega CV \\[ 5pt ] \end{eqnarray}
\] となる。したがって，電源を流れる電流\( \ \dot I \ \)は，
\[
\begin{eqnarray}
\dot I&=&{\dot I}_{\mathrm {R}}+{\dot I}_{\mathrm {L}}+{\dot I}_{\mathrm {C}} \\[ 5pt ] &=&\frac {V}{R}+\frac {V}{\mathrm {j}\omega L}+\mathrm {j}\omega CV \\[ 5pt ] &=&\left( \frac {1}{R}+\frac {1}{\mathrm {j}\omega L}+\mathrm {j}\omega C\right) V \\[ 5pt ] \end{eqnarray}
\] となる。題意より，\( \ R≫\omega L \ \)なので，\( \ \displaystyle \frac {1}{R}≪\frac {1}{\omega L} \ \)となり，
\[
\begin{eqnarray}
\dot I&=&\left( \frac {1}{R}+\frac {1}{\mathrm {j}\omega L}+\mathrm {j}\omega C\right) V \\[ 5pt ] &≃&\left( \frac {1}{\mathrm {j}\omega L}+\mathrm {j}\omega C\right) V \\[ 5pt ] &=&\left( -\mathrm {j}\frac {\omega C}{2}+\mathrm {j}\omega C\right) V \\[ 5pt ] &=&\mathrm {j}\frac {\omega CV}{2} \\[ 5pt ] \end{eqnarray}
\] と求められ，電流は電圧より\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)進みとなり，ベクトル図はウ，波形はカとなる。