《理論》〈電気及び電子計測〉[H19:問14]電圧計と電流計を用いた直流電力の誤差に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，電圧計と電流計を用いて抵抗負荷の直流電力を測定する場合について述べたものである。

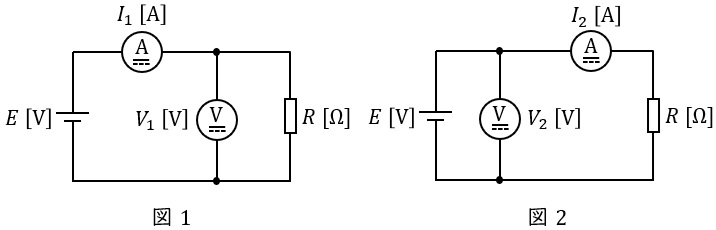
電源\( \ E \ \mathrm {[V]} \ \)，負荷抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，内部抵抗\( \ R_{v} \ \mathrm {[\Omega ]} \ \)の電圧計及び内部抵抗\( \ R_{a} \ \mathrm {[\Omega ]} \ \)の電流計を，それぞれ図1，図2のように結線した。図1の電圧計及び電流計の指示値はそれぞれ\( \ V_{1} \ \mathrm {[V]} \ \)，\( \ I_{1} \ \mathrm {[A]} \ \)，図2の電圧計及び電流計の指示値はそれぞれ\( \ V_{2} \ \mathrm {[V]} \ \)，\( \ I_{2} \ \mathrm {[A]} \ \)であった。

図1の回路では，測定で求めた電力\( \ V_{1}I_{1} \ \mathrm {[W]} \ \)には，計器の電力損失\( \ \fbox {　（ア）　} \ \mathrm {[W]} \ \)が誤差として含まれ，図2の回路では，測定で求めた電力\( \ V_{2}I_{2} \ \mathrm {[W]} \ \)には，同様に\( \ \fbox {　（イ）　} \ \mathrm {[W]} \ \)が誤差として含まれる。

したがって，\( \ R_{v}=10 \ \mathrm {[k\Omega ]} \ \)，\( \ R_{a}=2 \ \mathrm {[\Omega ]} \ \)，\( \ R=160 \ \mathrm {[\Omega ]} \ \)であるときは，\( \ \fbox {　（ウ）　} \ \)の回路を利用する方が，電力測定の誤差率を小さくできる。

ただし，計器の電力損失に対する補正は行わないものとする。

上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる語句又は式として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　\displaystyle \frac {{V_{1}}^{2}}{R_{v}}　 & 　{I_{2}}^{2}R_{a}　 & 　図 \ 2　 \\
\hline
(2) & 　{I_{1}}^{2}R_{a}　 & 　\displaystyle \frac {{V_{2}}^{2}}{R_{v}}　 & 　図 \ 1　 \\
\hline
(3) & 　{I_{1}}^{2}R_{a}　 & 　\displaystyle \frac {{V_{2}}^{2}}{R_{v}}　 & 　図 \ 2　 \\
\hline
(4) & 　\displaystyle \frac {{V_{1}}^{2}}{R_{v}}　 & 　{I_{2}}^{2}R_{a}　 & 　図 \ 1　 \\
\hline
(5) & 　I_{1}{R_{a}}^{2}　 & 　\displaystyle \frac {{V_{2}}^{2}}{R_{v}}　 & 　図 \ 2　 \\
\hline
\end{array}
\]

【ワンポイント解説】

電圧計と電流計を用いた直流電力の誤差と誤差率を考える問題です。
しっかりと導出するためには（ウ）の空欄が非常に難易度が高い問題です。なかなか解法は思い浮かばないかもしれませんが，（ア）と（イ）の空欄は理解できるようにしておきましょう。

1.誤差及び誤差率の定義
真値を\( \ T \ \)，測定値を\( \ M \ \)とすると，誤差\( \ \varepsilon \ \)と誤差率\( \ ％\varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&M-T \\[ 5pt ] ％\varepsilon &=&\frac {M-T}{T} \times 100 \ [％] \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
(ア)
図1の電圧計に流れる電流\( \ I_{v} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{v} &=&\frac {V_{1}}{R_{v}} \\[ 5pt ] \end{eqnarray}
\] となるので，負荷抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に流れる電流\( \ I_{R} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{R} &=&I_{1}-I_{v} \\[ 5pt ] &=&I_{1}-\frac {V_{1}}{R_{v}} \\[ 5pt ] \end{eqnarray}
\] となる。よって真値\( \ P_{T1} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{T1} &=&V_{1}I_{R} \\[ 5pt ] &=&V_{1}\left( I_{1}-\frac {V_{1}}{R_{v}}\right) \\[ 5pt ] &=&V_{1}I_{1}-\frac {{V_{1}}^{2}}{R_{v}} \\[ 5pt ] \end{eqnarray}
\] となるので，測定電力\( \ V_{1}I_{1} \ \mathrm {[W]} \ \)との誤差\( \ \varepsilon _{1} \ \mathrm {[W]} \ \)は\( \ \displaystyle \varepsilon _{1}=\frac {{V_{1}}^{2}}{R_{v}} \ \)と求められる。

(イ)
図2の負荷抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に加わる電圧\( \ V_{R} \ \mathrm {[V]} \ \)は，分圧の法則より，
\[
\begin{eqnarray}
V_{R} &=&\frac {R}{R+R_{a}}V_{2} \\[ 5pt ] \end{eqnarray}
\] となるので，真値\( \ P_{T2} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{T2} &=&V_{R}I_{2} \\[ 5pt ] &=&\frac {R}{R+R_{a}}V_{2}I_{2} \\[ 5pt ] &=&\frac {R+R_{a}-R_{a}}{R+R_{a}}V_{2}I_{2} \\[ 5pt ] &=&V_{2}I_{2}-\frac {R_{a}}{R+R_{a}}V_{2}I_{2} \\[ 5pt ] &=&V_{2}I_{2}-\frac {R_{a}}{R+R_{a}}\left( R+R_{a}\right) I_{2}\cdot I_{2} \\[ 5pt ] &=&V_{2}I_{2}-R_{a} {I_{2}}^{2} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，測定電力\( \ V_{2}I_{2} \ \mathrm {[W]} \ \)との誤差\( \ \varepsilon _{2} \ \mathrm {[W]} \ \)は\( \ \displaystyle \varepsilon _{2}=R_{a} {I_{2}}^{2} \ \)と求められる。

(ウ)
図1の誤差率\( \ ％\varepsilon _{1} \ \mathrm {[％]} \ \)は，ワンポイント解説「1.誤差及び誤差率の定義」の通り，
\[
\begin{eqnarray}
％\varepsilon _{1} &=&\frac {\varepsilon _{1}}{P_{T1}}\times 100 \\[ 5pt ] &=&\frac {\displaystyle \frac {{V_{1}}^{2}}{R_{v}} }{\displaystyle V_{1}I_{1}-\frac {{V_{1}}^{2}}{R_{v}}}\times 100 \\[ 5pt ] &=&\frac {V_{1}}{\displaystyle R_{v}\left( I_{1}-\frac {V_{1}}{R_{v}}\right) }\times 100 \\[ 5pt ] &=&\frac {V_{1}}{R_{v}I_{1}-V_{1} }\times 100 \\[ 5pt ] &=&\frac {V_{1}}{R_{v}\left( I_{v}+I_{R}\right) -V_{1} }\times 100 \\[ 5pt ] &=&\frac {V_{1}}{\displaystyle R_{v}\left( \frac {V_{1}}{R_{v}}+\frac {V_{1}}{R}\right) -V_{1} }\times 100 \\[ 5pt ] &=&\frac {V_{1}}{\displaystyle V_{1}+\frac {R_{v}}{R}V_{1} -V_{1} }\times 100 \\[ 5pt ] &=&\frac {V_{1}}{\displaystyle \frac {R_{v}}{R}V_{1} }\times 100 \\[ 5pt ] &=&\frac {R}{R_{v}}\times 100 \\[ 5pt ] &=&\frac {160}{10\times 10^{3}}\times 100 \\[ 5pt ] &=&1.6 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となり，図2の誤差率\( \ ％\varepsilon _{2} \ \mathrm {[％]} \ \)は，ワンポイント解説「1.誤差及び誤差率の定義」の通り，
\[
\begin{eqnarray}
％\varepsilon _{2} &=&\frac {\varepsilon _{2}}{P_{T2}}\times 100 \\[ 5pt ] &=&\frac {R_{a} {I_{2}}^{2} }{V_{2}I_{2}-R_{a} {I_{2}}^{2} }\times 100 \\[ 5pt ] &=&\frac {R_{a} {I_{2}}^{2} }{\left( R+R_{a}\right) I_{2}\cdot I_{2}-R_{a} {I_{2}}^{2} }\times 100 \\[ 5pt ] &=&\frac {R_{a} {I_{2}}^{2} }{R{I_{2}}^{2}+R_{a}{I_{2}}^{2}-R_{a} {I_{2}}^{2} }\times 100 \\[ 5pt ] &=&\frac {R_{a} {I_{2}}^{2} }{R{I_{2}}^{2} }\times 100 \\[ 5pt ] &=&\frac {R_{a} }{R }\times 100 \\[ 5pt ] &=&\frac {2}{160}\times 100 \\[ 5pt ] &=&1.25 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となるので，誤差率が小さいのは図2と求められる。