Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
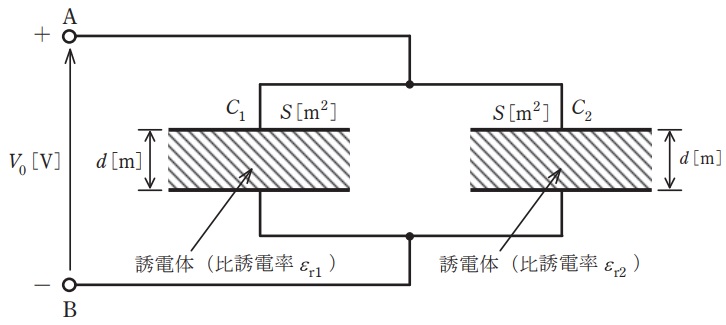
電極板面積と電極板間隔が共に\( \ S \ \mathrm {[m^{2}]} \ \)と\( \ d \ \mathrm {[m]} \ \)で,一方は比誘電率が\( \ \varepsilon _{\mathrm {r1}} \ \)の誘電体からなる平行平板コンデンサ\( \ C_{1} \ \)と,他方は比誘電率が\( \ \varepsilon _{\mathrm {r2}} \ \)の誘電体からなる平行平板コンデンサ\( \ C_{2} \ \)がある。今,これらを図のように並列に接続し,端子\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)間に直流電圧\( \ V_{0} \ \mathrm {[V]} \ \)を加えた。このとき,コンデンサ\( \ C_{1} \ \)の電極板間の電界の強さを\( \ E_{1} \ \mathrm {[V / m]} \ \),電束密度を\( \ D_{1} \ \mathrm {[C / m^{2}]} \ \),また,コンデンサ\( \ C_{2} \ \)の電極板間の電界の強さを\( \ E_{2} \ \mathrm {[V / m]} \ \),電束密度を\( \ D_{2} \ \mathrm {[C / m^{2}]} \ \)とする。両コンデンサの電界の強さ\( \ E_{1} \ \mathrm {[V / m]} \ \)と\( \ E_{2} \ \mathrm {[V / m]} \ \)はそれぞれ\( \ \fbox { (ア) } \ \)であり, 電束密度\( \ D_{1} \ \mathrm {[C / m^{2}]} \ \)と\( \ D_{2} \ \mathrm {[C / m^{2}]} \ \)はそれぞれ\( \ \fbox { (イ) } \ \)である。したがって,コンデンサ\( \ C_{1} \ \)に蓄えられる電荷を\( \ Q_{1} \ \mathrm {[C]} \ \),コンデンサ\( \ C_{2} \ \)に蓄えられる電荷を\( \ Q_{2} \ \mathrm {[C]} \ \)とすると,それらはそれぞれ\( \ \fbox { (ウ) } \ \)となる。
ただし,電極板の厚さ及びコンデンサの端効果は,無視できるものとする。また,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とする。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる式の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & {\displaystyle E_{1}=\frac {\varepsilon _{\mathrm {r1}}}{d}V_{0}} \atop {\displaystyle E_{2}=\frac {\varepsilon _{\mathrm {r2}}}{d}V_{0}} & {\displaystyle D_{1}=\frac {\varepsilon _{\mathrm {r1}}}{d}SV_{0}} \atop {\displaystyle D_{2}=\frac {\varepsilon _{\mathrm {r2}}}{d}SV_{0}} & {\displaystyle Q_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}} \atop {\displaystyle Q_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}} \\
\hline
(2) & {\displaystyle E_{1}=\frac {\varepsilon _{\mathrm {r1}}}{d}V_{0}} \atop {\displaystyle E_{2}=\frac {\varepsilon _{\mathrm {r2}}}{d}V_{0}} & {\displaystyle D_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0}} \atop {\displaystyle D_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0}} & {\displaystyle Q_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}} \atop {\displaystyle Q_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}} \\
\hline
(3) & {\displaystyle E_{1}=\frac {V_{0}}{d}} \atop {\displaystyle E_{2}=\frac {V_{0}}{d}} & {\displaystyle D_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}} \atop {\displaystyle D_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}} & {\displaystyle Q_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0}} \atop {\displaystyle Q_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0}} \\
\hline
(4) & {\displaystyle E_{1}=\frac {V_{0}}{d}} \atop {\displaystyle E_{2}=\frac {V_{0}}{d}} & {\displaystyle D_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0}} \atop {\displaystyle D_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0}} & {\displaystyle Q_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}} \atop {\displaystyle Q_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}} \\
\hline
(5) & {\displaystyle E_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}} \atop {\displaystyle E_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}} & {\displaystyle D_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0}} \atop {\displaystyle D_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0}} & {\displaystyle Q_{1}=\frac {\varepsilon _{0}}{d}SV_{0}} \atop {\displaystyle Q_{2}=\frac {\varepsilon _{0}}{d}SV_{0}} \\
\hline
\end{array}
\]
【ワンポイント解説】
比誘電率の異なる平行平板コンデンサの電界の強さ,電束密度及び蓄えられる電荷の大きさを求める問題です。
平成21年問1にも全く同じ問題が出題されています。やや古い過去問まで対策されていた方が有利な問題であったかなと思います。
1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて,蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には,
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
2.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \),極板の面積を\( \ S \ \mathrm {[m^{2}]} \ \),極板間の距離を\( \ d \ \mathrm {[m]} \ \)とすると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行平板コンデンサに電圧\( \ V \ \mathrm {[V]} \ \)をかけると,極板間の電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係
極板間の誘電率を\( \ \varepsilon \ \mathrm {[F / m]} \ \)とすると,電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)と電界\( \ E \ \mathrm {[V / m]} \ \)には,
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
解答:(4)
(ア)
両コンデンサに加わる電圧が\( \ V_{0} \ \mathrm {[V]} \ \),電極板間隔が共に\( \ d \ \mathrm {[m]} \ \)であるから,両コンデンサの電界の強さ\( \ E_{1} \ \mathrm {[V / m]} \ \)及び\( \ E_{2} \ \mathrm {[V / m]} \ \)は,ワンポイント解説「3.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」の通り,
\[
\begin{eqnarray}
E_{1}&=&\frac {V_{0}}{d} \\[ 5pt ]
E_{2}&=&\frac {V_{0}}{d} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(イ)
両コンデンサの電束密度\( \ D_{1} \ \mathrm {[C / m^{2}]} \ \)及び\( \ D_{2} \ \mathrm {[C / m^{2}]} \ \)は,ワンポイント解説「4.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係」の通り,
\[
\begin{eqnarray}
D_{1}&=&\varepsilon _{0}\varepsilon _{\mathrm {r1}}E_{1} \\[ 5pt ]
&=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0} \\[ 5pt ]
D_{2}&=&\varepsilon _{0}\varepsilon _{\mathrm {r1}}E_{2} \\[ 5pt ]
&=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(ウ)
両コンデンサの静電容量\( \ C_{1} \ \mathrm {[F]} \ \)及び\( \ C_{2} \ \mathrm {[F]} \ \)は,ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り,
\[
\begin{eqnarray}
C_{1} &=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}} S}{d} \\[ 5pt ]
C_{2} &=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}} S}{d} \\[ 5pt ]
\end{eqnarray}
\]
であるから,各コンデンサに蓄えられる電荷\( \ Q_{1} \ \mathrm {[C]} \ \)及び\( \ Q_{2} \ \mathrm {[C]} \ \)は,ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り,
\[
\begin{eqnarray}
Q_{1} &=&C_{1}V_{0} \\[ 5pt ]
&=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0} \\[ 5pt ]
Q_{2} &=&C_{2}V_{0} \\[ 5pt ]
&=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは